CINÉTICA ENZIMÁTICA
Cinética Enzimática
Estudo da velocidade de uma reação química que
ocorre na presença de uma enzima
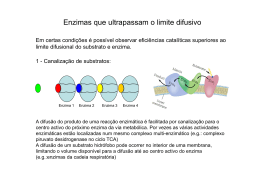
Velocidade vs. Concentração
A concentração de substrato influencia a velocidade de uma reação
Estudo da relação entre a concentração e a velocidade:
. No início da reação a quantidade de substrato é constante, já que a
quantidade de substrato é muito maior do que a de enzima.
.Determina-se a velocidade inicial de reação, Vo ,para uma
determinada [S].
.Obtêm-se valores para várias concentrações de substrato, mantendo
constante a concentração de enzima.
Assim podemos traçar os valores num gráfico, em que exprimimos
Vo como função de [S]
Velocidade vs. Concentração
Dados:
•Para [S] baixas, Vo aumenta quase linearmente
•Para [S] maiores, Vo aumenta mais gradualmente
•Para [S] mais elevadas, atinge-se uma velocidade máxima, Vmáx.
Equação de Michaelis-Menten
Comportamento é explicado pela formação do complexo enzima-substrato ES
1. O enzima liga-se ao substrato reversivelmente formando o complexo ES
Reação
rápida
E + S
k1
ES
k2
2. O complexo ES dissocia-se em enzima livre e produto da reação
Reação
mais lenta
ES
k3
E + P
.A reação 2, mais lenta, limita a velocidade global da reação.
.A velocidade é proporcional à concentração do complexo ES.
.A cada momento a enzima existe na forma livre e no complexo ES.
.A velocidade máxima (Vmáx) da reação ocorre quando todos as enzimas estão
associadas as moléculas de substrato.
Dedução da Equação Michaelis-Menten
A curva que representa a relação entre [S] e Vo tem forma idêntica para a
maioria das enzimas. Esta curva pode ser descrita algebricamente pela equação
de Michaelis-Menten.
A equação de Michaelis-Menten é
O passo limitante da velocidade das reações enzimáticas é a quebra do complexo ES
para formar o produto e a enzima livre.
Dedução da Equação Michaelis-Menten
Pressuposto: não há transformação de produto em substrato
Reações de formação e desassociação do complexo ES:
E + S
k1
k2
ES
k3
P + E
onde [E] e [S] são as concentrações da enzima e do substrato livres.
[ET] - concentração total da enzima
A concentração de enzima livre é, assim, [ET]-[ES]
Dedução da Equação Michaelis-Menten
E + S
k1
k2
ES
k3
P + E
Etapa 1:
velocidade de formação de ES = k1[E][S]
Etapa 2:
velocidade de decomposição de ES = k2[ES]
Etapa 3:
velocidade de consumo de ES = k3[ES]
velocidade de formação de P = k3[ES]
Velocidade de formação de ES é formada na etapa 1 e consumida nas
etapas 2 e 3.
velocidade de formação ES = k1[E][S] - k2[ES] - k3[ES]
[ES] é constante, ou seja, a velocidade de degradação e formação de ES são iguais.
Aplicando a aproximação do estado estacionário.
k1[E][S] = k2[ES] + k3[ES]
Dedução da Equação Michaelis-Menten
[E] = [ET]-[ES]
[S] ≈ [ST]
e
[S] = [ST] - [ES]
porque [ST] >>> [ET]
Substituindo na equação:
k1 ([ET] – [ES]) [S] = k2 [ES] + k3 [ES]
k1 [ET] [S] - k1 [ES] [S] = [ES] (k2 + k3)
k1 [ET] [S] = [ES] (k2 + k3) + k1 [ES] [S]
k1 [ET] [S] = [ES] {(k2 + k3) + k1 [S]}
 k1
É uma medida da estabilidade do
complexo enzima-substrato
Km = constante de Michaelis
Dedução da Equação Michaelis-Menten
velocidade inicial de formação de P é V0 = k3 [ES], então:
Vmáx
A velocidade é máxima quando [ES]=[ET]!
Esta forma da equação de Michaelis-Menten chama-se equação de Lineweaver-Burk
Equação de Lineweaver-Burk
Gráfico de 1/[V0] em função de 1/[S]
Coeficiente angular: Km/Vmáx
A intersecção da reta no eixo 1/V0 corresponde ao valor 1/Vmáx
Qdo y=0
1/V0 = 0; então a intersecção com o eixo 1/[S] corresponde a -1/Km