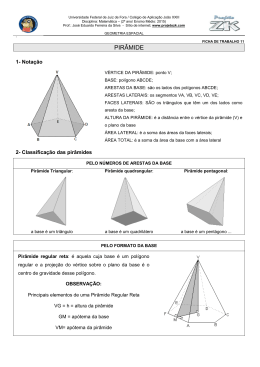
PAAES 2010-2013 2ª ETAPA Ao longo da história a arquitetura passou por
profundas e inovadoras mutações. A introdução
de novos materiais e técnicas da construção
civil revolucionaram os projetos arquitetônicos.
Apesar desse avanço tecnológico, muitas obras
do passado ainda surpreendem pela beleza e
precisão na sua elaboração, este é o caso das
famosas pirâmides egípcias. Hoje é comum encontrar, em grandes cidades, muitos edifícios
apresentando formas geométricas bem conhecidas em suas fachadas. As Figuras abaixo são
adaptações, respectivamente, de uma pirâmide
egípcia, de um arranha céu da cidade de São
Paulo e de um belíssimo orquidário recentemente inaugurado nessa mesma 3 cidade, onde
= 120 metros,
= 100 metros, EF é perpendicular a BC,
= t metros,
metros,
= 30 metros e
= (30 + r) metros, sendo
que h é a altura da pirâmide ABCDE e a área
lateral da pirâmide é igual à área lateral do
prédio representado na Figura 2.
Considerando as informações apresentadas,
marque, para as alternativas abaixo, (V) Verdadeira, (F) Falsa ou (SO) Sem Opção.
1 - (
2 - (
3 - (
4 - (
)
O volume da pirâmide ABCDE é igual
a 307200 m3.
) O valor de t é divisível por 5.
) Se r = 2 m, então a soma das áreas
das cúpulas esféricas (representadas na Figura 3) é maior ou igual a
30% da área lateral da pirâmide.
) Seja H o valor da área da região
plana, correspondente a metade da
coroa (ou anel) circular de raio r (em
metros), conforme vista frontal (em
preto), expressa na Figura 3. Logo,
se 0 < r ≤ 2, então H ≤ 62π m2.
Resolução:
1 - (F)
Tomando como O o pé da altura da
pirâmide ABCDE, temos que no triângulo EFO, retângulo em O:
(EF)2 (FO)2 (EO)2 100 2 60 2 h2 h 80m
(120)2 80
V
120 40 80 384000m3
3
2 - (V)
ALPIRÂMIDE ALPRISMA pg 4 t h 4(120)
100 4 t YT
2
Temos que
3
YT h e h2 60 2 100 2 2
3
h 80 e YT (80) 120m
2
Por fim:
240 100 4 t 120 t 50m , logo t
é divisível por 5.
3 - (F)
r = 2. Vamos determinar cada uma
das áreas:
AREA DAS CÚPULAS:
1
1
A C 4 (32 2 ) 4 (30 2 ) 4
4
A1 1024 900 1924 m2
AREA LATERAL DA PIRÂMIDE:
ALPIR p g (240)(100) 24000m 2
Em que p é o semi-perímetro e g é o
apótema da pirâmide.
1924. 30%.24000 A c 30%.A Lpir
4 - (V)
Teremos a área da coroa dada por:
H
1
124 ( (32 2 30 2 )) 64 2
2
Como 0 < r ≤ 2 segue que H ≤ 62π m2.
M
A
T
E
M
Á
T
I
C
A