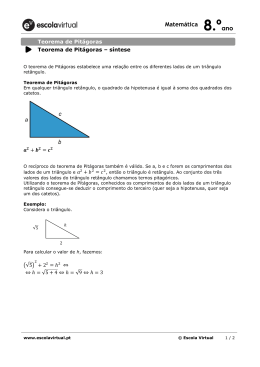
Teorema de Pitágoras
Recuperação 4º bimestre
Introdução


O teorema de Pitágoras é uma relação
matemática entre os três lados de qualquer
triângulo retângulo.
Em qualquer triângulo retângulo, o quadrado
do comprimento da hipotenusa é igual à
soma dos quadrados dos comprimentos dos
catetos.
Introdução

Sabendo-se então que no Teorema de
Pitágoras a hipotenusa é igual a soma dos
quadrados dos catetos. Na seguinte imagem
temos:
Portanto:
c² = b² + a²
Exercício 1:

Calcule o valor do segmento desconhecido
no triangulo retângulo a seguir:
Resolução:

x² = 9² + 12²
x² = 81 + 144
x² = 225
√x² = √225
x = 15
Exercício 2

Calcule o valor do cateto no triângulo
retângulo abaixo:
Resolução

x² + 20² = 25²
x² + 400 = 625
x² = 625 – 400
x² = 225
√x² = √225
x = 15
Exercício 3

Um ciclista acrobático vai atravessar um
prédio a outro com uma bicicleta especial,
percorrendo a distancia sobre um cabo de
aço, como demonstra o esquema a seguir:
Resolução

Isolando o triangulo ficará assim:

Então resolvemos:
x² = 10² + 40²
x² = 100 + 1600
x² = 1700
x = 41,23 (aproximadamente)

Exercício 4

Calcula o valor de x em cada um dos
triângulos retângulos:
A)

B)

Resolução


A) x² = 5² + 12²
x² = 25 + 144
x² = 169
x = 13
B) x² + 4,5² = 7,5²
x² + 20,25 = 56,25
x² = 56,25 – 20,25
x² = 36
x=6
Exercício 5

Calcule a área da figura:
Resolução


10² = h² + 5²
100 = h² + 25
h² = 100 – 25
h² = 75
h = 9 (aproximadamente)
A = [(22 + 12)/2] x 9
A = (34/2) x 9
A = 17 x 9 = 153
Fontes



http://pt.wikipedia.org/wiki/Teorema_de_Pit%
C3%A1goras
http://www.brasilescola.com/matematica/teor
ema-pitagoras.htm
http://pitagoras-upt.tripod.com/id7.html
Grupo - 1001




Danilo Lucas – 05
Diego Ribeiro – 06
Hiago Oliveira – 13
Leandro Barbosa – 18