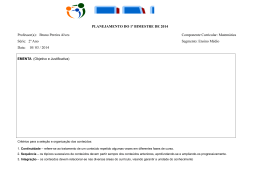
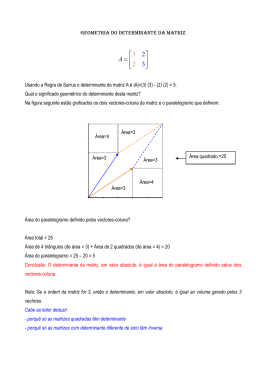
Exemplo 2:
Multiplicação de um número real por uma matriz
Dada uma matriz do tipo m x n e o número real k, o produto de k por A, que se indica por
k. A, é uma matriz do tipo m x n obtida pela multiplicação de cada elemento de A por k.
Exemplo:
Multiplicação de matrizes
Dada uma matriz A= (aij)m x n do tipo m x n e uma matriz B= (bij)m x n do tipo n x p, o
produto da matriz A pela matriz B é a matriz C= (cij)m x n do tipo m x p, tal que o elemento
cij é calculado multiplicando-se ordenadamente os elementos da linha i, da matriz A,
pelos elementos da coluna j, da matriz B, e somando-se os produtos obtidos.
- Para efetuar a multiplicação de duas matrizes, sempre multiplicamos as linhas da 1ª
matriz pelas colunas da 2ª.
- Só definimos o produto de A, B se o número de colunas de A for igual ao número de
linhas de B.
- O número de linhas da matriz produto C é igual ao número de linhas de A e o
número de colunas de C é igual ao número de colunas de B.
Exemplo:
Matriz inversa
Dada uma matriz A, quadrada de ordem n, se existir a matriz X, tal que: A.X = X.A= In,
então, X é denominada matriz inversa de A e é representada por A-1.
Exemplo:
Determinantes
É um número associado a uma matriz quadrada.
Indica-se o determinante da matriz quadrada A por det A ou A .
Só as matrizes quadradas possuem determinante,
Uma das mais importantes aplicações da teoria de determinante é na resolução de
sistemas lineares.
Determinante de uma matriz quadrada de ordem 1
Determinante de uma matriz quadrada de ordem 2
Exemplo:
Determinante de uma matriz quadrada de ordem 3
Consideremos a matriz genérica de ordem 3:
Esses produtos podem ser obtidos pela Regra de Sarrus, que consiste nos seguintes
passos:
1º passo: Copie as duas primeiras colunas após a terceira coluna, de forma a montar
uma nova matriz com 3 linhas e 5 colunas.
2º passo: Marque as três diagonais que descem.
3º passo: Marque as três diagonais que sobem. Os produtos obtidos nas diagonais que
sobem devem ter o sinal invertido.
4º passo: O determinante da matriz A é a soma dos seis produtos obtidos, conservados
os sinais.
Exemplo: