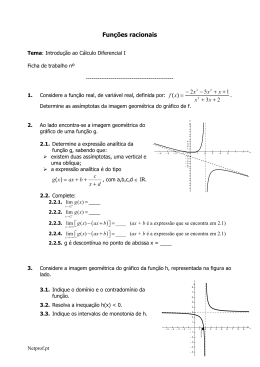
1.
Considere, em IR,
R, a família de funções tais que
f(x) =
b +
1
x − a
A figura representa a imagem geométrica de uma função h
dessa família. Então, os valores de a e b são:
(A)
(B)
(C)
(D)
2.
a = -1
a= 1
a= 2
a = -2
e
e
e
e
b=2
b = -2
b = -1
b=1
Sendo f uma função real de variável real definida por
f (x) =
2
, podemos concluir que a função g
x
−>
cujo o gráfico se obtém do da função f por uma translação associada ao vector
definida por:
2x + 4
x +1
2x
(C) g ( x ) =
x +1
(A)
3.
− 2x
x +1
− 2x + 4
(D) g( x ) =
x +1
g(x ) =
(B)
g(x ) =
De uma função de domínio [a,b] sabe-se
sabe se apenas que t.v.m[a,b]=0. Só com este conhecimento
podemos concluir que:
(A)
(B)
(C)
(D)
4.
u (−1,−2) é
A função é injectiva
A função é constante em todo o seu domínio
A função é não injectiva
A função é crescente no seu domínio.
Considere a funções f real de variável real
f (x) =
x 2 − 5x + 6
x−2
4.1. Identifique o domínio de f(x).
4.2. Escreva uma equação das assímptotas da função f.
2x 2 − 6x + 4
5. Considere a função f (x ) =
x2 − 4
5.1. Identifique o domínio da função
5.2. Estude a função f quanto à existência de assímptotas.
( )
5.3. Identifique lim x −>+∞ f x
5.4. Resolva algebricamente a inequação f(x)>2
6.
Considere a família de funções
i( x ) = ax +
1
.
x+b
Determine condições para os valores de a e b de modo que:
6.1. A família de funções tenha por assímptotas x=-1
x= 1 e a bissectriz dos quadrantes ímpares.
6.2. O
limx −>+∞ i(x ) = 0 e lim x − >0− i(x ) = −∞
7.
8.
Para cada uma das seguintes funções racionais determine, sempre que a questão faça sentido, o
domínio, os zeros, as assímptotas, uma representação gráfica e o contradomínio.
y=
7.2.
y = 2+
7.3.
y=
2
1− x
x+3
6 − 8x − 12x 3
x + x 2 − 2x 3
Resolva em IR cada uma das seguintes condições e confirme a solução usando a calculadora gráfica.
8.1.
9.
x −3
x − 7x + 12
7.1.
( x − 3)( x + 1) = 0
x −3
8.2.
4
3
−2 =
x −3
x
8.3.
3
1
1
=
−
x −1 x +1 1− x
8.4.
x2
<0
x +3
8.5.
1− x
≥0
( x − 2 )( x + 3)
2
O custo médio para produzir x unidades por dia numa indústria é dado, em euros, por:
500 + 2x + 0,1x 2
A(x) =
x
9.1. Faça um esboço do gráfico da função e escreva uma equação para cada uma das suas
assímptotas.
9.2. Resolva a condição e interprete o seu significado:
500 + 2x + 0,1x 2
< 10
x
9.3. Calcule o número de unidades x a produzir de modo que o custo médio por unidade seja de 20
euros.
9.4. Suponha que a empresa está a produzir por dia 200 unidades e que vai aumentar a produção
de t unidades.
9.4.1. Explique que o custo médio para produzir cada unidade a mais do que as 200 é dado por:
F( t) =
em que
C ( t ) − C ( 200 )
t − 200
C ( x ) = 500 + 2x + 0,1x 2
9.4.2. Escreva uma equação para as assímptotas do gráfico de F e interprete o significado das
mesmas.