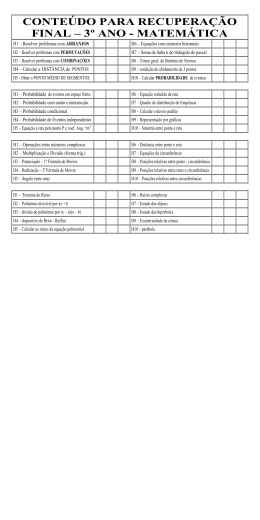
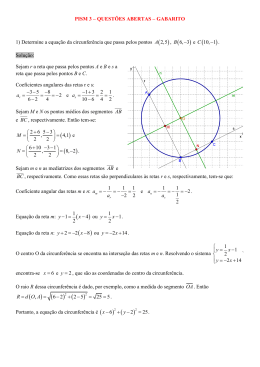
UNIVERSIDADE FEDERAL DE SANTA MARIA
COLÉGIO TÉCNICO INDUSTRIAL DE SANTA MARIA
PROJETO PEDAGÓGICO DE CURSO
CURSO TÉCNICO EM INFORMÁTICA PARA INTERNET
INTEGRADO AO ENSINO MÉDIO
COMPONENTES CURRICULARES
DISCIPLINA: Matemática
SIGLA: MAT
CARGA HORÁRIA: 120 horas
Ano: 3o Ano
OBJETIVOS





Aplicar os conhecimentos matemáticos para identificar e entender o impacto
das tecnologias no meio ambiente;
Reconhecer na matemática os fundamentos necessários para aplicar nas
diferentes disciplinas dos cursos técnicos;
Relacionar os fundamentos matemáticos com os conhecimentos das diversas
áreas e disciplinas;
Desenvolver o raciocínio lógico e a capacidade de questionar processos
naturais e tecnológicos;
Compreender a matemática como uma parcela do conhecimento humano, essencial
para a formação de todos os técnicos, que contribui para a construção de
uma visão do mundo, para ler e interpretar a realidade e para desenvolver
capacidades que deles serão exigidas ao longo de sua vida social e
profissional.
PROGRAMA
11.1
1.2
1.3
1.4
22.1
2.2
2.3
2.3.1
2.3.2
2.3.3
2.4
33.1
3.2
3.3
3.4
3.5
3.5.1
3.5.2
3.5.3
3.5.4
3.6
3.6.1
3.6.2
3.6.3
3.7
3.7.1
3.7.2
3.7.3
3.7.4
MATEMÁTICA FINANCEIRA
Porcentagem
Juro simples
Juro composto
Resolver problemas que envolvam juros simples e juros compostos
ESTATÍSTICA
Termos estatísticos: população, amostra e frequência
Tipos de gráficos: linha, setor e coluna. Construir e analisar gráficos
Medidas de tendência central
Moda
Mediana
Médias: Aritmética, ponderada e harmônica
Medidas de dispersão: Desvio Padrão, Variância
GEOMETRIA ESPACIAL
Poliedros: definição e elementos (Vértice, arestas e faces)
Relação de Euler
Poliedros de Platão
Poliedros regulares
Prismas
Definição e elementos dos prismas retos, oblíquos e regulares
Secção transversal
Superfície lateral e total
Volume
Cubo
Definição e elementos
Superfície lateral e total
Volume
Pirâmide
Definição e elementos
Classificação
Relações métricas numa pirâmide
Superfície lateral, total e volume
3.7.5 Secção transversal
3.8
Cilindro
3.8.1 Definição e elementos
3.8.2 Classificação (oblíquo e reto)
3.8.3 Secção meridiana
3.8.4 Secção transversal
3.8.5 Cilindro equilátero
3.8.5.1 Superfície lateral, total e volume
3.9
Cone
3.9.1 Definição e elementos
3.9.2 Classificação (oblíquo e reto)
3.9.3 Secção meridiana
3.9.4 Secção transversal
3.9.5 Superfície lateral, total e volume
3.10 Esfera
3.10.1 Definição e elementos
3.10.2 Secção plana de uma esfera
3.10.3 Pólos
3.10.4 Área da superfície esférica
3.10.5 Volume
4GEOMETRIA ANALÍTICA
4.1
Coordenadas cartesianas
4.2
Distância entre dois pontos
4.2.1 Associar cada par ordenado a um único ponto do plano cartesiano,
determinar a distância entre dois pontos
4.3
Condições de alinhamento de três pontos
4.4
Área de triângulo
4.4.1 Estabelecer a condição de alinhamento de três pontos e resolver
problemas que envolvam área do triângulo em função de seus vértices
4.5
Equação geral da reta
4.6
Intersecção de retas
4.7
Formas de reta (geral, reduzida, segmentária e paramétrica)
4.8
Coeficiente angular e linear
4.9
Equação da reta dado um ponto e a direção
4.9.1 Reconhecer e estabelecer as diversas formas de equação de uma reta
4.10 Condição de paralelismo e perpendicularismo
4.11 Posições relativas de duas retas
4.12 Ângulo entre duas retas
4.12.1 Resolver problemas de intersecção, posições relativas e ângulos entre
duas retas
4.13 Distância entre ponto e reta
4.14 Distância entre duas retas
4.15 Circunferência
4.15.1 Definição
4.15.2 Equação geral da circunferência
4.15.3 Reconhecimento de equação de uma circunferência
4.15.4 Posições relativas (ponto e circunferência; reta e circunferência;
circunferência e circunferência
4.15.4.1 Determinar os coeficientes angular e linear, a distância entre reta
e ponto e entre duas retas
4.15.4.2 Identificar posições relativas da circunferência
5FUNÇÃO POLINOMIAL
5.1
Definição
5.2
Grau de um polinômio
5.3
Identidade de polinômio (nulo e idêntico)
5.3.1 Identificar uma função polinomial, seu grau e seus coeficientes
5.4
Operações com polinômios (adição, subtração, multiplicação e divisão)
5.4.1 Divisão (método dos coeficientes a determinar)
5.4.2 Divisão por polinômio de 1º grau
5.4.2.1 Teorema do resto
5.4.2.2 Dispositivo prático de Briott-Ruffini
5.5
Decomposição de um polinômio em fatores do 1º grau
5.5.1 Efetuar operações com polinômios e verificar identidades
5.5.2 Resolver problemas envolvendo as operações com polinômios, decomposição
e o teorema do resto
5.6
5.7
5.8
Multiplicidade de uma raiz
Raízes complexas
Determinar as raízes de uma equação polinomial
PROCEDIMENTOS METODOLÓGICOS E RECURSOS DIDÁTICOS




Aulas expositivas;
Projetos;
Exercícios teóricos;
Trabalho de pesquisa.
AVALIAÇÃO
A avaliação estará centrada na análise do processo de aprendizagem e não
apenas no julgamento dos resultados de operações cognitivas de memorização. Serão
realizados debates, seminários, relatórios de pesquisa, viagens técnicas e provas
com e sem consulta aos materiais didáticos.
Basear-se-á no Sistema de Avaliação do curso, aprovado pelos órgãos
competentes.
BIBLIOGRAFIA
BIBLIOGRAFIA BÁSICA
BIANCHINI, Edwaldo & PACCOLA, Herval. Curso de Matemática – Ensino Médio. São
Paulo: Moderna, 2003.
V. Único. Matemática 2º Grau. São Paulo: Moderna, 1990; 3v.
BONGIOVANI, Vincenzo; VISSOTO LEITE, Olímpio Rudinir e LAUREANO, José Luiz
Tavares. Matemática 2º Grau. São Paulo: FTD, 1994.
DANTE, Luiz Roberto. Matemática: Contexto e Aplicações. São Paulo: Ática,
2003. V. Único.
GIOVANNI, José Ruy & BONJORNO, José Roberto. Matemática 2º Grau. São Paulo:
FTD, 1992. 3v.
PAIVA, Manoel Rodrigues. Matemática: Conceitos, Linguagem e Aplicações. São
Paulo: Moderna, 2002. Único.
SMOLE, Kátia Stocco; DINIZ, Maria Ignez. Matemática - Ensino Médio. São
Paulo: Saraiva, 2005.
BIBLIOGRAFIA COMPLEMENTAR
FERNANDES, Vicente Paz & YOUSSEF, Antônio Nicolau. Matemática para o colégio
– 2º Grau. São Paulo: Scipione, 1987.
GENTIL, Nélson et al. Matemática para o 2º Grau. São Paulo: Ática, 1990. 3v.
IEZZI, Gelson. Matemática Elementar. 5 ed. São Paulo: Atual, 1993. 10v.
MACHADO, Antônio Santos. Matemática – Temas e Metas. São Paulo: Atual, 1986.
6v.
MARCONDES, Carlos Alberto dos Santos; NELSON, Gentil; GRECO, Sérgio Emílio.
Matemática: Novo Ensino Médio. 7 ed. São Paulo: Ática, 2003. Único.
NETTO, Scipione di Pierro & ALMEIDA, Nilze Silveira de. Matemática – Curso
Fundamental 2º Grau. São Paulo: Scipione, 1990. 3v.
SIGNORELLI, Carlos Francisco. Matemática 2º Grau. São Paulo: Ática, 1992. 3v.
XAVIER, Claudio da Silva & BARRETO, Benigno Filho. Matemática Aula por Aula.
São Paulo: FTD, 2005.