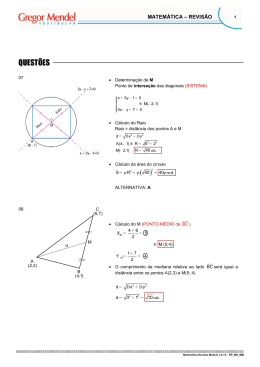
Questão 83
CURSO E COLÉGIO
Um aluno precisa localizar o centro de uma moeda circular e, para tanto, dispõe apenas de um lápis, de
uma folha de papel, de uma régua não graduada, de um compasso e da moeda.
Nessas condições, o número mínimo de pontos distintos necessários de serem marcados na
circunferência descrita pela moeda para localizar seu centro é
(A) 3.
(B) 2.
(C) 4.
(D) 1.
(E) 5.
Alternativa: A
CURSO E COLÉGIO
Considerando 3 pontos distintos da circunferência, tracemos o triângulo ABC como
mostra a figura:
Construimos então a reta mediatriz relativa ao segmento BC da seguinte forma:
1º Com a ponta seca do compasso no vértice B traça-se um arco de circunferência.
Repete-se o processo no vértice C.
2º Pelos pontos B’ e C’ traça-se a reta r (mediatriz do segmento BC)
3º Repete-se a construção para a reta s, reta mediatriz relativa do lado AC.
O ponto de interseção entre essas duas retas (r e s) é o circuncentro do triângulo ABC,
ou seja, obtemos o centro da moeda.