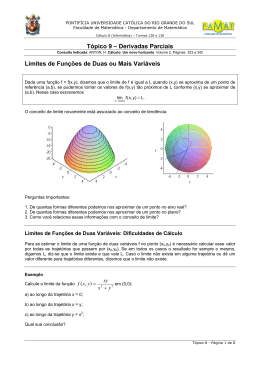
Funções de várias variáveis
Funções de várias variáveis
Derivadas Parciais de ordens superiores
Calculam-se as derivadas parciais de ordem superior computando as
derivadas parciais das funções já derivadas. Essas derivadas são
derivadas obtidas parcialmente e de uma ordem a menos.
Exemplo
Calcule as derivadas parciais de segunda ordem da função f(x,y) =
2x3.e5y.
Temos que:
f
x
f
y
( x , y )  6 x .e
2
5y
( x , y )  10 x .e
3
5y
Funções de várias variáveis
Portanto, a segunda derivada, em relação a x é:
 f
2
x
2
( x , y )  12 x .e
5y
E a segunda derivada, em relação a y é:
 f
2
y
2
( x , y )  50 x .e
3
5y
Funções de várias variáveis
Ainda podemos calcular a segunda derivada da derivada parcial em
relação a y, calculada agora em relação a x:
 f
2
xy
( x, y ) 

3
x
(10 x e
5y
)  30 x .e
2
5y
E a segunda derivada da derivada parcial em relação a x, calculada
agora em relação a y:
 f
2
yx
( x, y ) 

y
2
(6 x e
5y
)  30 x .e
2
5y
Funções de várias variáveis
Derivadas Parciais de ordens superiores
As duas primeiras derivadas parciais apresentadas acima são
chamadas de puras ;
As duas últimas são chamadas de mistas.
Funções de várias variáveis
Notação
Se z=f(x,y), podem-se computar quatro derivadas parciais de
segunda ordem com suas respectivas notações de acordo
com as expressões abaixo:
 z
 z
2
x
2

 z
x x
 z
2
y
2
 z

y y
2
xy
 z

2
yx
 z xx ( x , y )  f xx ( x , y )

 z
x x
 z
y x
 z yy ( x , y )  f yy ( x , y )
 z yx ( x , y )  f yx ( x , y )
 z xy ( x , y )  f xy ( x , y )
Funções de várias variáveis
Derivadas Parciais de ordens superiores
Em nosso exemplo as duas últimas derivadas (as mistas) deram o
mesmo resultado. Isto não é coincidência. A igualdade ocorre
desde certas condições sejam satisfeitas.
Funções de várias variáveis
Derivadas Parciais de ordens superiores
Em nosso exemplo as duas últimas derivadas (as mistas) deram o
mesmo resultado. Isto não é coincidência. A igualdade ocorre
desde certas condições sejam satisfeitas.
Proposição
Se f(x,y) está definida numa certa vizinhança de (x0,y0) e é tal que as
derivadas
vizinhança, então
f
,
f
 f
2
,
x y xy
 f
2
xy
 f
2

yx
 f existem
2
e
.
yx
e são contínuas nessa
Funções de várias variáveis
Regra da Cadeia
A regra da cadeia para funções de várias variáveis tem o intuito de
calcular derivadas parciais de funções compostas de várias
variáveis.
Suponha que a função P = p(x,y) com derivadas parciais contínuas
represente a quantidade produzida de um determinado bem a
partir de matérias-primas x e y, que por sua vez, variam com o
tempo, ou seja, x = x(t) e y = y(t).
Funções de várias variáveis
A quantidade produzida expressa-se como função do tempo, de
acordo com a seguinte expressão:
P = p(x(t) , y(t)) = P(t)
A regra da cadeia para a composição desta natureza é dada por:
  p  dx   p  dy
P ' (t )  

.
.
  x  dt   x  dt
Funções de várias variáveis
Exemplo
Considere uma firma cuja receita expressa-se através da função
R(x,y) = xy2, onde x e y representam as quantidades de dois
bens produzidos. Suponha que estas quantidades dependam do
capital k e do trabalho l, de acordo com as funções x = 4k + 3l
e y = 3k + l. Calcule as derivadas parciais da receita em relação
ao capital e ao trabalho, como funções de tais variáveis.
Antes de aplicar a Regra da Cadeia, precisamos calcular as seguintes
derivadas parciais:
 R  R  x  x.  y  y
,
,
,
,
e
x y k l k l
Funções de várias variáveis
Exemplo
R
x
R
y
x
k
x
l
y
k
y
l
 y  ( 3 k  1)
2
2
 2 xy  2 ( 4 k  3l )( 3 k  1)
4
3
3
1
Funções de várias variáveis
Exemplo
Aplicando a Regra da Cadeia, temos:
R
k
R
l


R x
x k
R x
x l


R y
y k
R y
y l
 ( 3 k  l ) . 4  2 ( 4 k  3l )( 3 k  l ). 3
2
 ( 3 k  l ) . 3  2 ( 4 k  3l )( 3 k  l ). 1
2
Funções de várias variáveis
Aplicação
A temperatura no ponto (x,y) de uma placa de metal situada no
plano XY é dada por: T = 10.(x2 + y2)2.


Determine a taxa de variação de T em relação à distância no
ponto (-1, 2) e na direção de do eixo Y;
Partindo-se do ponto (-1, 2) e deslocando-se na direção do
eixo X a temperatura aumenta ou diminui?
Funções de várias variáveis
Solução
T
y
T
x
 20 ( x  y ) 2 y  40 y ( x  y )
2
2
2
2
 20 ( x  y ) 2 x  40 x ( x  y )
2
2
2
2
T
y
T
x
(1, 2 )  20 (1  2 ) 2 . 2  40 . 2 (1  2 )  400
2
2
2
2
(  1, 2 )  20 [(  1)  2 ] 2 .(  1)   200
2
2
Funções de várias variáveis
Curvas de nível
Para traduzir um gráfico de z = f(x,y) em curvas de nível, basta
esboçar as curvas-intersecção de f(x,y) com z = c, para
diferentes valores de c.
Exemplo-1
Reconhecer e representar graficamente o gráfico da função
z = f(x,y) = x2 + y2.
Fazendo z=c, desde que c > 0, obtemos a equação: x2+y2=c. Isto
significa que a projeção no plano xy da curva-intersecção do
plano horizontal z = c com o gráfico da função possui tal
equação. Essa projeção é a circunferência de centro na origem e
raio
.
Como o corte z = c é um círculo, o gráfico desta função é um
parabolóide de revolução obtido pela rotação da parábola z = x2
em torno do eixo z.
Funções de várias variáveis
Exemplo 1
Funções de várias variáveis
Exemplo 1
Funções de várias variáveis
Exemplos de outras curvas
Funções de várias variáveis
Exemplos de outras curvas
Funções de várias variáveis
Gradiente de uma função
O gradiente de uma função f(x,y) num ponto (x0,y0), designado por
f(x0,y0) ou grad f(x0,y0), é o vetor livre cujas coordenadas são:
f
x
( x0 , y0 )
e
f
y
( x0 , y0 )
Funções de várias variáveis
Simbolicamente:
 f

f
 f ( x0 , y0 )  
( x 0 , y 0 ),
( x0 , y0 )
y
 x

Exemplo 2
Calcule o gradiente da função f(x,y) = 3x2y-x2/3.y2 no ponto (1,3).
Funções de várias variáveis
Resolução
Calculemos a derivada parcial da função f(x,y) em relação a x e y:
f
x
( x 0 , y 0 )  6 xy 
No ponto (1,3):
f
x
f
y
2
f
1
x
3
y
2
y
3
2
( x0 , y0 )  3 x  2 x 3 y
 f

f
 f (1,3 )  
(1,3 ),
(1,3 ) 
y
 x

(1,3 )  6 . 1 . 3 
2
1
(1)
3
( 3 )  18  6  12
2
3
2
(1,3 )  3 (1)  2 (1) 3 ( 3 )   3
2
Portanto, o gradiente da função f(x,y) no ponto (1,3)
é o vetor f(1,3)=[12,-3].
2
Funções de várias variáveis
Gradiente de uma função
Convenciona-se representar este vetor com origem no ponto em relação
ao qual se calcula o gradiente.
Funções de várias variáveis
Gradiente de uma função
Dessas considerações é possível pensar num campo de vetores
gradiente de uma função, que podem ser representados
geometricamente por um conjunto de vetores que fornecem em
cada ponto distinto do plano o vetor gradiente da função.
Funções de várias variáveis
Relação entre Gradiente Curvas de Nível
Dizemos que um vetor u é ortogonal a uma curva plana, dada pelas
equações paramétricas x = x(t) e y = y(t), se ele é ortogonal ao
vetor [x’(t), y’(t)], que é o vetor tangente à curva.
Teorema
O gradiente de uma função f(x,y) no ponto (x0,y0) é ortogonal à
curva de nível da função que passa por esse ponto.
Funções de várias variáveis
Prova
Os pontos (x,y) sobre uma curva de nível podem ser parametrizados
por uma variável t: x = x(t) e
y = y(t);
Como f(x0,y0) = C, então, f(x(t),y(t)) = C;
Derivando ambos os membros da igualdade em relação a t, obtemos,
pela regra da cadeia:
f
x
[ x ( t ), y ( t )]. x ' ( t ) 
f
y
[ x ( t ), y ( t )]. y ' ( t )  0
Funções de várias variáveis
Prova
O primeiro membro dessa igualdade é o produto escalar dos vetores
f(x(t),y(t)) e [x’(t),y’(t)];
Mas, [x’(t),y’(t)] é o vetor tangente à curva de nível no ponto
(x(t),y(t));
Portanto, o gradiente da função f no ponto (x,y) é ortogonal ao vetor
tangente à curva de nível no ponto (x,y).