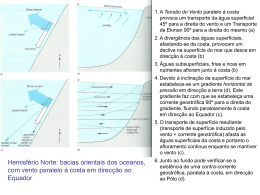
Meteorologia Sinótica Conceitos Gerais. Movimentos Atmosféricos (Aspectos Físicos e Observações) Revisão de Conceitos Básicos Forças Fundamentais Sistema de Equações Atmosféricas (noções matemática) Ventos Teóricos Geostrófico, Gradiente, Ciclostrófico, térmico Variação vertical do vento Ventos Observados Ventos locais Ventos Globais Estrutura de Altas e Baixas Pressões Movimentos Atmosféricos Geração Transformação Destruição Atmosfera Energia Cinética Energia Potencial Atmosfera Fonte de Calor Sol Calor Movimentos Atmosféricos Movimentos Atmosféricos Circulação Atmosférica Movimentos Atmosféricos Medidos; Eficientes transportadores de Calor, Massa e Momentum Componente Horizontal z y Ventos Componente Vertical Freqüentemente estimados, são importantes para formação de nuvens e chuvas x Conceitos Básicos Velocidade Angular Taxa de giro de um sistema em torno de um ponto de referência. No caso da Terra: S ___ =V t e ___ = t Como S = r , V = r Raio da terra Velocidade Linear Velocidade Angular da terra ~ 7,3x 10-5 rad/s Conceitos Básicos Força Centrípeta Para um corpo deslocar-se em trajetória curva (mudando a direção) e mantendo constante o módulo do vetor velocidade, alguma torça deverá estar continuamente atuando sobre o mesmo, para modificar a direção do vetor velocidade. Admitindo V1 = V2 = V (em módulo) a t = V a ___ ___ = V t Como ___ = , Sinal negativo, a é t dirigido p/ o centro O a=V= Aceleração da Partícula 2 V2 ___ V= r a = - 2 r Na forma Vetorial Primeira lei de Newton, um corpo em movimento continuará em movimento, com velocidade constante, a menos que uma força resultante externa atue sobre ele. Conceitos Básicos Conservação O momento angular de um sistema do Momento permanece constante, a menos que seja Angular aplicado um torque externo a esse sistema Considerando uma partícula em movimento circular com V cte L= r x m V = r . mV . sen(90°) j Tomando-de o módulo de L por unidade de massa L = r V= r2 Pela lei da conservação do momento angular A força centrípeta é única força responsável por esse movimento circular (velocidade cte em módulo), é dirigida para a origem e não imprime torque à partícula r aumenta, V diminui ( r V ) é Cte r diminui, V aumenta Conceitos Básicos Experiência, pessoa girando uma pedra presa a um fio que se enrola com o tempo... t=1 V2 t=2 t=3 V3 V1 Pela lei da conservação do momento angular r aumenta, V diminui ( r V ) é Cte r diminui, V aumenta Conceitos Básicos Conservação No caso da Terra, parcelas de ar giram em do Momento eixos perpendiculares ao eixo de rotação Raio da Terra Angular Latitude L = Rt2 cos2 () Exemplo 1: Parcela no Equador, em repouso em relação a superfície da Terra V = Rt Exemplo 2: Se essa parcela é forçada a se deslocar até 60N, pela lei da conservação do momento angular: V´ = V / cos() V´ = V / cos(60) V´ = 2V parcela, inicialmente em repouso no equador, terá uma velocidade na direção oeste-leste (em relação à Terra) cada vez maior, ao se desloca em direção aos pólos FORÇAS FUNDAMENTAIS QUE ATUAM NA ATMOSFERA Segunda lei de Newton Taxa de variação do "momentum" (quantidade de movimento) de um sistema é igual à soma de todas as forças que nele atuam Forças preponderantes na atmosfera gravitacional devida ao gradiente de pressão Referencial inercial (estrelas fixas) fricção Considerando a rotação da Terra: coriolis força centrífuga Referencial não-inercial (forças "aparentes" devem ser adicionadas para que a segunda lei de Newton possa a ser aplicada ) FORÇAS FUNDAMENTAIS QUE ATUAM NA ATMOSFERA Gravitacional Força de atração exercida pela Terra sobre um corpo de massa m sobre a superfície. Orientada p/ o centro da Terra. Centrífuga Surge exclusivamente devido a rotação da Terra, para equilibrar o sistema. Coriolis Ocorre quando um corpo se movimenta em relação a um referencial não inercial (Terra em rotação). Gradiente de Pressão Existe devido a diferença de pressão. Orientada das altas pressões paras as baixas pressões (contrário do gradiente) Fricção Devido a “rugosidade” da Terra. Atua no sentido de frear os movimentos atmosféricos próximo a superfíie da Terra. Sistema de Equações Atmosféricas Movimentos Atmosféricos governados por 3 princípios básicos: Conservação de massa, momentum e energia Equação do Movimento (momentum) 1 dV 2xV p g * Fr dt Equação da Continuidade (massa) 1 ddp .V 0 dt Equação da Energia Termodinâmica cv dT d cp q dt dt * Força Centrípeta combinada com a gravitacional (energia) Equação do Movimento Conservação de momentum Aceleração do movimento 1 dV * 2xV p g Fr dt Gravidade Coriolis k Vz j Gradiente Pressão V Vx i V y j Vz k V Vy Vx i * Força Centrípeta combinada com a gravitacional Fricção Análise de Escala Parâmetros típicos de Escala sinótica Sinótica Componente X Componente Y U ~ 10 ms-1 p/ ~ 103 ms-2 W ~ 10-2 ms-1 L/U ~ 105s L ~ 106 m a ~ 107m D ~ 104 m fo ~ 10-4 A B C D E F du -2vsen + 2wcos + uw - uvtg = -1p dt a a x + vw - u2tg = -1p a a y dv -2usen dt U2 foU foW UW 10-4 10-3 10-6 10-8 U2 10-5 p 10-3 Vento Geostrófico Aproximação Balanço entre a força de coriolis e do Geostrófica gradiente de pressão Baixa Fp Vg Fco HN Alta Holton (1979) • Vento gira paralelo as isóbaras ou isoípsas (igual geopotencial) deixando valores mais altos a esquerda (HS) • Aproximação geostrófica em latitudes média permite estimar vento com erro de 10 a 15% • Não tem aplicação prática na Região Tropical Vento Gradiente Aproximação Balanço entre a força de coriolis e do gradiente de pressão e centrífuga Gradiente Fp B HN Fco Fce Fco A Fp Fco Equador • Torna-se mais fraco próximo ao centro de Alta pressão • Melhor aproximação do vento em regiões tropicais (ex: Ciclones tropicais) Vento Ciclostrófico Aproximação Balanço entre a força gradiente de pressão Ciclostrófica e centrífuga Fp B HN Fco Fce Equador • caso particular do vento gradiente (Coriolis é desprezada em relação ao gradiente de pressão). • escoamento atmosférico curvo com escala horizontal pequena (Ex: tornados – raio ~300m e ventos fortes ~ 30m/s = 108Km/h) • Só pode ocorrer em torno de uma BAIXA PRESSÃO • Em pequenos vórtices (redemoinhos) coriolis não é importante Vento Térmico VT = Vg1 – Vg2 Diferença entre o vento geostrófico de dois níveis de pressão (superior (1) – inferior (2)) Z2 (1000 hPa) 0 100 200 300 400 500 600 Z1 (500 hPa) 5.300 5.400 5.500 5.600 5.700 -Vg2 Vg1 VT Vg2 5.800 5.500 5.400 5.300 5.200 5.100 5.000 4.900 Espessura entre 1000 e 500 hPa • Sopra paralelo as isotermas (isolinhas de espessura) • Somente existe se houver um gradiente horizontal de temperatura • Tem a mesma direção das isolinhas de espessura (1000-500) • Deixa AR FRIO a DIREITA e AR QUENTE a ESQUERDA - HS Variação do vento com a Altura Conhecendo campo de temperatura e vento Vg1 = VT + Vg2 numa superfície mais baixa (p2) posso estimar Vg1 na superfície mais alta Advecção Quente Situação 1 Situação 2 0 +1 0 0 0 +1 T0 +2 VT VT T0 +1 Vg2 Vg1 T0 +4 T0 +2 Vg2 Vg1 T0 T0 • Advecção Quente (fria): ângulo entre Vg2 e Vg1 sofreu uma variação anti-horária (horária) no HS. Inverso no HN. • Advecção fria: temperatura da camada diminui rapidamente c/ altura, gerando instabilidade • Advecção Quente: temperatura aumenta c/ altura, estabilidade Exemplos Ar Quente VT Vento Gradiente VT VT Vento Geostrófico Ar Frio VT VT Exemplos Vento Geostrófico Vento Gradiente Exemplos Giro horário: advecção fria Vg1 Vg2 Vg2 Vg1 Giro anti-horário: advecção quente Equação da Continuidade Conservação de massa Variação da pressão com o tempo d 1 dp .V 0 dt Termo de Divergência Redução da densidade (aquecimento ou redução pressão) d/dt < 0 Convergência de massa . V < 0 é constante* Sem convergência ou divergência Aumento da densidade (resfriamento ou aumento da pressão) d/dt < 0 * Considerando o ar incompressível ( é constante) Divergência de massa . V > 0 Exemplos ETA
Baixar