Balanceamento de Carga e Detecção de
Terminação
Balanceamento de carga e detecção de
terminação
• Balanceamento de carga
– utilizado para distribuir o processamento entre os processadores (ou
processos) de modo a obter a maior velocidade possível de execução
• Detecção de terminação
– utilizada para determinar quando um processamento chega ao seu fim e é
especialmente mais difícil de implementar quando a computação é
distribuída
Balanceamento estático
• Nesse tipo, a tentativa de balanceamento de carga
ocorre antes da execução de qualquer processo
• Algumas técnicas potenciais:
– algoritmo round-robin
• distribui as tarefas na ordem seqüencial dos processadores, voltando
ao primeiro quando todos processadores tiverem recebido uma tarefa
– algoritmos aleatórios
• seleciona os processadores de forma aleatória para executar as tarefas
– bisecção recursiva
• divide recursivamente o problema em subproblemas de igal esforço
computacional enquanto tenta minimizar a quantidade de troca de
mensagens
– simulated annealing, genetic algoritms
• técnicas de otimização
Problemas com o balanceamento estático
• Difícil estimar com precisão os tempos de execução das
várias partes de um programa sem realmente executálas
• Atrasos de comunicação que variam sob circunstâncias
diferentes
• Alguns problemas possuem um número indeterminado
de passos para atingir a sua solução
Balanceamento dinâmico
• Realizado durante a execução do processo
• Os problemas indicados para o balanceamento estático
são levados em consideração, fazendo-se com que a
divisão da carga dependa da execução das partes do
programa à medida que elas são executadas
• Provoca um overhead maior na execução do
programa,mas geralmente é mais eficiente que o
balanceamento estático
Processos e processadores
• A computação é dividida em tarefas a serem realizadas,
que são executadas por processos mapeados em
processadores
• O objetivo é manter os processadores ocupados a maior
parte do tempo possível
• Geralmente mapeamos um único processo em um
processador, então utilizaremos os termos processo e
processador de alguma forma indiscriminada
Balanceamento dinâmico
• Duas classificações:
– centralizado
• as tarefas são manipuladas de uma localização central
• existe uma clara estrutura mestre-escravo
– não-centralizado
• as tarefas são circuladas por entre processos arbitrários
• uma coleção de processos trabalhadores opera sobre um problema e
interage entre eles, reportando o resultado final a um único processo
• um processo trabalhador pode receber tarefas de outros processos
trabalhadores e pode enviar tarefas para outros processos
trabalhadores
Balanceamento dinâmico centralizado
• Um processo mestre mantém a coleção de tarefas a
serem executadas
• As tarefas são enviadas para os processos escravos pelo
processo mestre
• Quando um processo mestre finaliza sua tarefa, pede
uma nova para o processo mestre
• Termos utilizados: repositório(pool) de trabalho,
trabalhadores replicados, fazenda de processadores
Terminação
• A computação deve ser parada quando a solução for
atingida
• Quando as tarefas são retiradas de uma fila de tarefas,
a computação termina quando:
– a fila de tarefas está vazia E
– todos os processos pediram uma nova tarefa e nenhuma nova tarefa foi
gerada
• A condição da fila estar vazia não é suficiente porque
podem existir processos sendo executados que podem
gerar novas tarefas para a fila
• Em algumas aplicações, o escravo pode detectar a
condição de término do programa por uma condição de
término local, tal como encontrar um item em um
algoritmo de procura
Mecanismos de transferência de tarefas Iniciado pelo receptor
• Um processo seleciona um outro processo e pede tarefas
a ele
• Tipicamente, um processo pede tarefas a outro,quando
ele tem poucas ou nenhuma tarefa a executar
• Se mostrou eficiente para sistemas com carga alta
• Pode ser muito custoso determinar a carga de cada
processo
Mecanismos de transferência de tarefas Iniciado pelo processo que envia
• Um processo seleciona um outro processo e envia
tarefas para ele
• Tipicamente, um processo com uma carga pesada passa
algumas tarefas a outro, que estiver disposto a recebêlas
• Se mostrou eficiente para sistemas com carga leve
• Pode se misturar os dois métodos
• Mas é custoso determinar a carga dos processos
• Em sistemas muito carregados, o balanceamento de
carga pode ser difícil de ser atingido por falta de
processos disponíveis
Algoritmos para seleção de processo para
método descentralizado
• Algoritmo round-robin
– o processo Pi pede tarefas ao processador Px , onde x é dado por um
contador que é incrementado depois de cada pedido, utilizando aritmética
módulo n (quando existem n processos), excluindo x = I
• Algoritmo de polling aleatório
– o processo Pi pede tarefas ao processo Px, onde x é um número
selecionado aleatoriamente entre 0 e n-1 (excluindo i)
Balanceamento de carga utilizando um
estrutura de pipeline
• O processo mestre alimenta a fila com tarefas em uma
extremidade e as tarefas são deslocadas para o final da
fila
• Quando um processo trabalhador, Pi (1 <= i < n)
detecta uma tarefa na sua entrada da fila e o processo
está inativo, ele pega a tarefa da fila
• As tarefas à esquerda são arrastadas ao longo da fila de
modo a preencher o lugar deixado pela tarefa e uma
nova tarefa é inserida na extremidade esquerda da fila
• Ao final, todos os processos pegarão uma tarefa e a fila
será preenchida com novas tarefas
• Tarefas de maior prioridade ou tamanho podem ser
colocadas em primeiro lugar na fila
Código utilizando compartilhamento de
tempo entre computação e comunicação
• Processo mestre
for (i = 0; i < no_tasks; i++) {
recv(P1, request_tag);
send(&task, P1, task_tag);
}
recv(P1 , request_tag);
send (&empty, P1 , task_tag);
Código utilizando compartilhamento de
tempo entre computação e comunicação
• Processo Pi (1<i<n)
if (buffer == empty) {
send(Pi-1, request_tag);
recv(&buffer, Pi-1, task_tag);
}
if ((buffer == full) && (!busy))
task = buffer;
buffer = empty;
busy = TRUE;
}
nrecv(Pi+1, request_tag, request); /* não bloqueante p/ testar mens. da direita */
if (request && (buffer == full)) {
send (&buffer, Pi+1);
buffer = empty;
}
if (busy) {
faça algum trabalho da tarefa
se a tarefa acabou, atribua o valor false a busy
}
Rotinas de recebimento não bloqueantes
PVM
• A rotina pvm_nrecv() retorna o valor zero se nenhuma
mensagem foi recebida
• A rotina pvm_probe() pode ser utilizada para verificar
se uma mensagem foi recebida sem ter que ler a
mensagem
• Depois, utiliza-se a rotina recv() para ler a mensagem e
desempacotá-la
Rotinas de recebimento não bloqueantes
MPI
• A rotina não bloqueante MPI_Irecv() retorna um
identificador de requisição, que pode ser utilizado em
rotinas subseqüentes para esperar por mensagens ou
para descobrir se a mensagem já foi realmente recebida
no ponto de chamada da rotina (MPI_Wait() e
MPI_Test(), respectivamente)
• Essa rotina coloca um pedido por uma mensagem e
retorna imediatamente
Algoritmos distribuídos para detecção de
terminação - condições de terminação
• Condições de terminação em um determinado tempo t :
– as condições locais de terminação específicas da aplicação existem em
uma coleção de processos no tempo t
– não existem mensagens em trânsito entre os processo no tempo t
• A diferença entre essas condições de terminação e
aquelas para o esquema centralizado é ter que levar em
conta as mensagens em trânsito
• A segunda condição é necessária porque uma
mensagem em trânsito pode reinicializar um processo
terminado
• Mais difícil de ser reconhecida a terminação
• O tempo para o trânsito das mensagens entre processos
não é previamente conhecido
Algoritmos distribuídos para detecção de
terminação - mensagens de confirmação
• Cada processo está em um dos dois estados :
– inativo
– ativo
• O processo que enviou uma tarefa para um outro
processo de modo que ele entrou no estado ativo se
torna pai desse processo
• Quando um processo recebe uma tarefa de um outro
processo, que não seja seu pai, ele envia uma mensagem
de confirmação
• Ele só envia uma mensagem de confirmação para o pai
quando ele estiver pronto para se tornar inativo, isto é :
– existe a condição local de terminação
– as confirmações para todas as mensagens recebidas foram enviadas
– as confirmações de todas as mensagens enviadas foram recebidas
Algoritmos distribuídos para detecção de
terminação - algoritmo do anel em passo
único
• Quando P0 termina, ele gera um sinal que é passado
para P1
• Quando Pi (1<= i < n) recebe o sinal e já terminou, ele
passa o sinal para Pi+1. Caso contrário, ele espera por
sua condição de terminação local e quando a atinge
passa o sinal para Pi+1. Pn-1 passa o sinal para P0
• Quando P0 recebe o sinal de volta, ele sabe que todos os
processos do anel terminaram, e uma mensagem
informando o término global pode ser enviada a todos
os processos
• O algoritmo assume que um processo não pode ser
reativado após ter atingido sua condição de terminação
local (não se aplica a problemas com pool de trabalho)
Algoritmos distribuídos para detecção de
terminação - algoritmo do anel em dois
passos
• Pode tratar processos reativados mas requer duas
passagens pelo anel
• Caso um processo Pi passe uma tarefa para Pj, onde j <
i depois do sinal de terminação ter passado por Pj,
necessita-se circular o sinal de terminação novamente
ao longo do anel
• Para diferenciar as duas situações, colorem-se os sinais
e os processos de branco e preto
• Quando um sinal preto é recebido significa que uma
terminação global pode não ter ocorrido e o sinal tem
que percorrer o anel novamente
Algoritmo do anel em dois passos
• P0 se torna branco quando termina e gera um sinal
branco para P1
• O sinal é passado através do anel de um processo para
outro assim que o processo termine. Se Pi passa uma
tarefa para Pj onde j<i, ele se torna um processo preto,
caso contrário ele é um processo branco. Um processo
preto colore um sinal de preto e o passa a frente, e um
processo branco passa o sinal para frente com a cor
original recebida. Depois que Pi passa o sinal, ele se
torna um processo branco. Pn-1 passa o sinal para P0
• Quando o processo P0 recebe um sinal preto, ele passa
um sinal branco e se ele recebe um sinal branco, todos
os processos terminaram
Algoritmo da energia fixa
• O sistema inicia com a energia toda em um processo
denominado mestre
• O mestre passa partes da energia junto com as tarefas
enviadas aos processos que pediram tarefas
• Se esses processos recebem pedidos de tarefas, a
energia é dividida em mais partes e passada aos
processos
• Quando um processo fica inativo, ele envia a energia de
volta antes de pedir uma nova tarefa
• Um processo não envia de volta sua energia até que a
energia que ele enviou seja retornada e combinada com
a energia total que ele possui
Problema do caminho mínimo
• Dado um conjunto de nós conectados por ligações que
possuem um peso associado a elas, encontre o caminho
de um nó específico para outro nó específico de modo
que ele apresente a menor soma acumulada de pesos
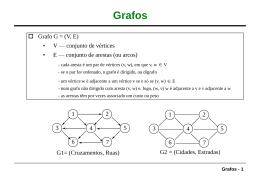
• Os nós conectados podem ser descritos por um grafo,
onde os nós são chamados de vértices e as ligações de
arestas
• Se as arestas só podem ser atravessadas em uma
direção, denominamos o grafo de grafo direcionado
Problema do caminho mínimo - Aplicações
• A menor distância entre duas cidades ou outros pontos
do mapa, onde os pesos representam distâncias
• A rota mais rápida para viajar, onde os pesos
representam os tempos
• A maneira mais barata de viajar de avião, onde os
pesos representam os custos dos vôos entre as cidades
• A melhor rota para enviar uma mensagem entre
computadores de modo a se obter um atraso mínimo no
envio
• O melhor modo de subir uma montanha dado um
mapa do terreno com os seus contornos
Representação de grafos
• Matriz de adjacências
– um array bidimensional a, onde cada elemento a[i][j] armazena o peso
associado à aresta entre o vértice i vértice j, se ela existir
• Lista de adjacências
– para cada vértice existe uma lista de vértices diretamente conectadas ao
vértice por uma aresta e os pesos correspondentes de cada aresta
• Matriz de adjacências são utilizadas para grafos densos
• Lista de adjacências são utilizadas para grafos esparsos
• As duas estruturas podem requerer espaços de
armazenamento diferentes
• Acesso à lista de adjacências mais lento que acesso à
matriz de adjacências
Procura do menor caminho em grafos
• Dois algoritmos conhecidos com uma única fonte:
– Moore (1957)
– Dijkstra (1959)
• Algoritmo de Moore mais fácil de paralelizar
• Os pesos devem ser todos positivos
Algoritmo de Moore
• Iniciando com um vértice fonte, utiliza-se o seguinte
algoritmo para se avaliar um vértice i:
– encontre a distância ao vértice j através do vértice i e a compare com a
menor distância corrente ao vértice j
– troque a menor distância, caso a distância através do vértice i seja menor,
ou seja, dj=min(dj,di+wi,j), onde di é a distância corrente do nó fonte para o
vértice i e wi,j é o peso da aresta entre o vértice i e o vértice j
Algoritmo de Moore - Estruturas de dados
e código
• Uma fila do tipo primeiro-a-entrar-primeiro-a-sair
para armazenar a lista de vértices a serem examinados
(inicialmente somente o vértice fonte está na fila)
• A menor distância corrente do vértice fonte ao vértice i
será armazenada em um array dist[i] que são
inicializadas com o valor infinito (onde temos n
vértices, 1 <= i < n e vértice 0 é o vértice fonte)
• Suponha que w[i][j] armazene o peso da aresta entre os
vértices i e j e considere o código abaixo:
newdist_j = dist[i] + w[i[[j];
if (new_dist_j < dist[j]) dist [j] = newdist_j;
• Quando uma menor distância é encontrada para o
vértice j, adiciona-se esse vértice à fila (se já não
estiver) que vai fazer com que esse vértice seja
examinado novamente
Código seqüencial
• A rotina next_vertex () retorna o próximo vértice da
fila ou o valor no_vertex, caso fila vazia
• Utiliza-se uma matriz de adjacências denominada w[][]
while ((i = next_vertex()) != no_vertex)
for (j = 0; j < n; j++)
if (w[i][j] != infinity) {
newdist_j = dist[i] + w[i[[j];
if (new_dist_j < dist[j]) {
dist [j] = newdist_j;
append_queue(j);
}
}
Implementação paralela com pool
centralizado de trabalho
• O pool mantém a fila de vértices e envia vértices para
cada escravo
• Cada escravo obtém vértices da fila de vértices e envia
novos vértices
• Como a estrutura utilizada para armazenar os pesos
das arestas do grafo é fixa, pode-se copiá-la para cada
escravo
Código para o mestre
while (vertex_queue() != empty) {
recv (PANY, source = Pi);
v = get_vertex_queue();
send(&v, Pi);
send(&dist, &n, Pi);
.
recv(&j, &dist[j], PANY, source=Pi);
append_queue(j, dist[j]);
};
recv(PANY, source=Pi);
send(Pi, termination_tag);
Código para o escravo (processo i)
send (Pmaster);
recv(&v, Pmaster, tag);
if (tag != termination_tag) {
recv(&dist, &n, Pmaster);
for (j = 0; j < n; j++)
if (w[v][j] != infinity) {
newdist_j = dist[v] + w[v][j];
if (newdist_j < dist[j]) {
dist[j] = newdist_j;
send(&j, &dist[j], Pmaster);
}
}
}
Pool de trabalho descentralizado
• Cada processo escravo i procura somente em volta do
vértice i e possui uma entrada para esse vértice na fila
de vértices caso ele exista na fila
• O array dist[] será distribuído entre os processos de
modo que o processo i mantenha a mínima distância
corrente para o vértice i
• O processo i também armazena a matriz/lista de
adjacências para o vértice i, para identificar as arestas
que saem do vértice i
Algoritmo de procura
• O vértice fonte é carregado no processo apropriado
• O vértice A é o primeiro vértice a ser analisado e o
processo a ele associado é ativado
• Esse processo procura menores distâncias aos vértices
conectados a esse vértice
• A distância ao vértice j será enviada ao processo j para
que ele compare com o seu valor correntemente
armazenado e o atualize caso seja maior
• Todas as menores distâncias são atualizadas durante
uma procura
• Se os conteúdos de d[i] mudam, o processo i será
reativado para realizar o processo de procura
novamente
Código para escravo (processo i)
recv(newdist, PANY);
if (newdist < dist) {
dist = newdist;
vertex_queue = TRUE;
} else vertex_qeue = TRUE;
if (vertex_queue == TRUE)
for (j = 0; j < n; j++)
if (w[j] != inifnity ) {
d = dist + w[j];
send (&d, Pj);
}
Código para escravo simplificado
(processo i)
recv(newdist, PANY);
if (newdist < dist) {
dist = newdist;
for (j = 0; j < n; j++)
if (w[j] != inifnity ) {
d = dist + w[j];
send (&d, Pj);
}
}
Mecanismo de terminação
• Mecanismo necessário para repetir as ações e terminar
quando todos os processos estiverem inativos e realizar
o tratamento das mensagens em trânsito
• Solução simples: utilize o envio de mensagens síncrono,
no qual o processo não pode continuar enquanto o
destino não tiver recebido a mensagem
• Um processo ó está ativo quando um vértice estiver na
fila, e é possível que vários processos fiquem inativos
levando a uma solução ineficiente
• O método é praticamente impraticável para um grafo
muito grande se somente um vértice for alocado para
cada processador, deve-se utilizar um grupo de vértices