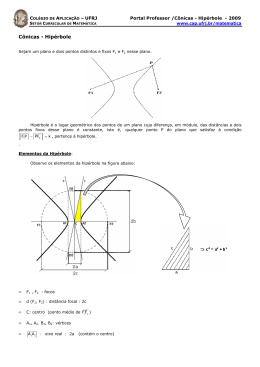
Cônicas
Porque Cônicas?
Parábola
Considere uma reta d e um ponto f não
pertencente a d
 Parábola é o conjunto dos pontos cuja
distância ao ponto f é igual a distância
deste ponto à reta d

Graficamente
P
F
v
A
P’
d

Seja P’ o pé da reta perpendicular a d que
passa por P
Assim P pertence à parábola se e
somente se
 d(F,P)=d(P,P’) -> |FP|=|P’P|

Notações
F-> foco
 d-> reta diretriz
 Eixo -> reta que passa pelo foco e é
perpendicular à diretriz
 Vértice (v) -> Ponto de interseção entre a
parábola e o eixo
 A-> interseção do eixo com a diretriz

Por definição de parábola, se P = v então
 d(v,f)=d(v,a)=p/2, p-> parâmetro da
parábola

Encontrar a equação da parábola

Eixo da parábola = eixo y

V(0,0)

|FP|=|PP’|

PP’ = (x-x,y+p/2)=(0,y+p/2)
FP = (x-0,y-p/2) =(x,y-p/2)


|(x,y-p/2) |=|(0,y+p/2)|
2
p
x  y  py 
4
2

2
X2=2py ou y = X2/2p

2
p
y 2  py 
4
Estudo da Parábola
Se 2py=x2 -> 2py >=0 -> p e y tem sinais
iguais
 Caso 1: p>=0 -> y>=0 -> concavidade
para cima


Caso 2: p<=0 -> y<=0 -> concavidade
para baixo

Eixo da parábola = eixo x

V(0,0)

|FP|=|P’P|
P’P = (x+p/2,y-y)=(x+p/2,0)
FP = (x-p/2,y-0) =(x-p/2,y)
y2=2px



Estudo da Parábola
Como y2 >=0 então 2px>=0. Logo p e x
tem sinais iguais
 Caso 1: p >= 0 -> x >= 0 -> concavidade
para direita


Caso 2: p <= 0 -> x <= 0 -> concavidade
para esquerda
Exercício

Determinar a equação da parábola v(0,0)
e diretriz d:y=-2
Exercicio

Determinar a equação da parábola com
foco F(2,0), diretriz d:x+2=0

Determinar a equação da parábola com
foco F(0,-3), e v(0,0)

Determinar a equação da parábola com
foco V(0,0), simétrica em relação ao eixo
dos y e passando pelo ponto P(2,-3)
Determinar Vértice, foco, equações da
reta diretriz e eixo
 X2=-12y

Determinar Vértice, foco, equações da
reta diretriz e eixo
 y2-x=0

Vértices fora da origem
V(a,b)
 Eixo paralelo ao eixo y
 (x-a)2=2p(y-b)
 Eixo paralelo ao eixo x
 (y-b)2=2p(x-a)

Exercício

Determine a equação da parábola V(-2,3),
F(-2,1)

Determine a equação da parábola F(2,3) e
diretriz y=-1

Determine a equação da parábola V(1,3),
eixo paralelo ao eixo x passando pelo
ponto P(-1,-1)
Equação explícita da parábola
A equação da parábola de vértice V(a,b) e
eixo paralelo ao eixo y tem a forma
(x-a)2=2p(y-b)
 x2-2ax+a2=2py-2pb
 y=(x2-2ax+a2+2pb)/2p
 Esta última é a forma explícita da parábola

Exercício

Ache o vértice, o foco, a diretriz e o eixo
de simetria da parábola x2+4x+8y+12
Exercício

Ache o vértice, o foco, a diretriz e o eixo
de simetria da parábola y2+4y+16x-44
Exemplo

Ache o vértice, o foco, a diretriz e o eixo
de simetria da parábola y2-12x-12=0
Exemplo

Ache o vértice, o foco, a diretriz e o eixo
de simetria da parábola 8x=y2-6y+10
Elipse
Uma elipse de focos F e F’ é o conjunto
dos pontos cuja soma das distâncias a F e
F’ é igual a uma constante que indica-se
por 2a
 Portanto, P є Elipse se, e somente se,
d(P,F)+d(P,F’)=2a

Equação
Caso 1: F(-c,0) e F’(c,0), c>=0
 Olhando para o triângulo PFF’ vemos que
o lado F’F mede 2c e é menor que a soma
dos outros dois lados, medindo 2a

P
a
F
a
c
F’
c
Logo, c<a
 Nota: quanto mais a se aproxima de c,
mais achatada fica a elipse, logo a
excentricidade (e) cresce


e=c/a, 0<e<1
Elementos
Focos: são os pontos F e F’
 Distância Focal = 2c
 Centro = ponto médio do segmento FF’
 Eixo Maior: segmento A1A2 medindo 2a
 Eixo Menor é o segmento B1B2 de
comprimento 2b onde b2=a2-c2


De acordo com a definição, P(x,y) є elipse
se, e somente se, |PF’|+|PF|=2a
( x  c) 2  y 2  ( x  c) 2  y 2  2a
Equação

Desenvolvendo a equação anterior obtemse
x2/a2+y2/b2=1

Eixo maior sobre o eixo x focos sobre o
eixo x
Equação

Caso 2: Focos F(0,c) e F’(0,-c)

Analogamente
x2/b2+y2/a2=1
Equação

Caso 3: centro fora da origem C(x0,y0)
Eixo maior//eixo x: (x-x0)2/a2 +(y-y0)2/b2=1
 Eixo maior//eixo y: (x-x0)2/b2 +(y-y0)2/a2=1

Exercício
Determinar os vértices A1 e A2, focos e
excentricidade
 X2/100+y2/36=1
 x2+25y2=25
 4x2+25y2=1

Exercício
Determinar a equação da elipse
 Eixo maior mede 10, focos (4,0) e (-4,0)

Exercício
Determinar a equação da elipse
 Centro C(0,0) um foco F(3/4,0) e um
vértice A(1,0)

Exercício
Determinar a equação da elipse
 Centro C(0,0), F(c,0), F’(-c,0), P(-2(5)1/2,2)

Exercício
Determinar a equação da elipse
 Centro C(0,0), focos no eixo x, e=2/3 e
P(2,-5/3)

Exercício
Determinar a equação da elipse
 Centro C(2,4), um foco F(5,4) e=3/4

Exercício
Determinar a equação da elipse
 Centro C(-3,0), um foco F(-1,0), a elipse é
tangente ao eixo y

Exercício
Determinar a equação da elipse
 Centro C(-3,4), semi-eixos de
comprimento 4 e 3, eixo maior // ao eixo y

Exercício
Determinar a equação da elipse
 Centro C(2,-1), tangente aos eixos
coordenados e eixos de simetria (eixo
maior e eixo menor) paralelos aos eixos
coordenados

Exercício
Determinar centro, vértices A1 e A2 e
excentricidade
 4x2+9y2-8x-36y+4=0

Hipérbole
Sejam dois pontos fixo F1 e F2 com
d(F1,F2)=2c
 A hipérbole é o conjunto dos pontos P(x,y)
do plano tais |d(F1,P)-d(F2,p)|=2ª


Com 2ª<2c
P
F1
F2
Da equação anterior tem-se
 d(F1,P)-d(F2,p)= ±2a
 Quando P estiver no ramo da direita,
d(F1,P)>d(F2,p) -> d(F1,P)-d(F2,p)= 2a
 Quando P estiver no ramo da esquerda,
d(F1,P)<d(F2,p) -> d(F1,P)-d(F2,p)=-2a

Seja o segmento de reta F1F2 e chame
de A1 e A2 a interseção de F1F2 com a
hipérbole
 Considere outra reta perpendicular a esta
passando pelo ponto médio C de F1F2

F1
A1
C
A2
F2

A hipérbole é simétrica em relação a:
 Segmento
F1F2
 Eixo vertical
 Ponto C

Ainda pela simetria, d(A1,F1)=d(A2,F2)

Qual é o valor de d(A1,A2)?
Se P=A2, da def de hipérbole |d(F1,A2)d(F2,A2)|=2a
 Como A2 está no ramo direito, (F1,A2)d(F2,A2)=2a


Pela figura vemos que
d(F1,A2)=d(F1,A1)+d(A1,A2)
M
N
F1
A1
P
r
θ
C
A2
F2
Q
s

Pela figura vemos que
d(F1,A2)=d(F1,A1)+d(A1,A2)
Substituindo
d(F1,A1)+d(A1,A2)- d(F2,A2)=2a

Logo d(A1,A2) =2a
Elementos da hipérbole






Focos F1 e F2
Distância Focal: d(F1,F2)=2c
Centro Ponto médio de F1F2
Vértices: A1,A2
Eixo Real: segmento A1A2 e |A1A2|=2ª
Eixo imaginário: Segmento B1B2 onde de
comprimento 2b onde b vem da relação
C2=a2+b2

MNPQ é um retângulo inserido no círculo
de raio c

r e s são assíntotas da hipérbole

r passa pelo ponto C e tem inclinação b/a

s passa por ponto C e tem inclinação –b/a

\theta abertura da hipérbole

e=c/a excentricidade da hipérbole
 Note
que e está relacionado com a abertura
\theta da hipérbole




Na figura anterior fixando c e aumentando a
vemos que a abertura da hipérbole diminui
Menor a abertura menor a excentricidade e>1
Maior a abertura maior a excetrencidade
Quando a=b, dizemos que a hipérbole é
equilátera
Equação
Caso 1: Eixo real sobre o eixo x e C(0,0)
 Obs: determinaremos a equação do ramo
direito: F1(-c,0),F2(c,0) e P(x,y)
 d(F1,P)-d(F2,P)=2a
 d(F1,P) =2a+d(F2,P)
 |F1P| =2a+|F2P|

((x+c)2+y2)1/2=2a+((x-c)2+y2)1/2
 x2+2xc+c2+y2=4a2 -4a((x-c)2+y2)1/2+x22xc+c2+y2
 4xc- 4a2 = -4a((x-c)2+y2)1/2
 xc- a2 = -a((x-c)2+y2)1/2
 x2c2-2xca2+a4=a2x2-2xca2+a2c2+a2y2

x2c2-a2x2-a2y2=a2c2-a4
 x2(c2-a2)-a2y2=a2(c2-a2)
 x2b2-a2y2=a2b2


x2/a2-y2/b2=1

Centro C(0,0) eixo real sobre o eixo x
Observações
Se P(x,y) estivesse no ramo esquerdo,
então Q(-x,y) estaria no ramo direito de
modo que ainda valeria a igualdade
anterior
 Quando o eixo real estiver sobre o eixo y
a equação será: y2/a2-x2/b2=1

Analogamente
Quando C(x0,y0) e o eixo real // eixo x
 (x-x0)2/a2-(y-y0)2/b2=1

Quando C(x0,y0) e eixo real // eixo y
 (y-y0)2/a2-(x-x0)2/b2=1

Equação das assíntotas
y-y0 = m(x-x0) m é a inclinação
 r:m=b/a; s:m=-b/a

Exemplo

Determinar vértices, focos, excentricidade
e esboçar o gráfico: x2-y2=1
Exemplo

Determinar vértices, focos, excentricidade
e esboçar o gráfico: -4x2+y2=1
Exemplo

Determinar vértices, focos, excentricidade
e esboçar o gráfico: -4x2+2y2=1
Exemplo

Determinar a equação da hipérbole que
satisfaz as seguintes condições:
 Focos
F(±5,0), Vértices (±3,0)
 Eixo real = eixo x, centro C(0,0)
Exemplo

Determinar a equação da hipérbole que
satisfaz as seguintes condições:
 a=4,
Vértices (±4,0)
 Passa por P(8,2), centro C(0,0)
Exemplo

Determinar a equação da hipérbole que
satisfaz as seguintes condições:
 b=8,
e=5/3
 Eixo real =eixo y, centro C(0,0)
Exemplo

Determinar a equação da hipérbole que
satisfaz as seguintes condições:
 Assintotas
y=±2x, Vértices (±3,0)
Exemplo

Determinar a equação da hipérbole que
satisfaz as seguintes condições:
 Um
foco em (7,-2), Vértices (5,-2) e 3,-2
Exemplo

Determinar a equação da hipérbole que
satisfaz as seguintes condições:
C
(5,1), um foco F(9,1) eixo imaginário méde
4(2)1/2
Exemplo

Determinar a equação da hipérbole que
satisfaz as seguintes condições:
C
(2,-3), eixo real // eixo y passando por (3,-1)
e (-1,0) (conferir a solução)