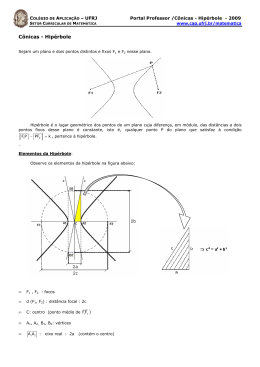
2-A hipérbole
1
d  F1 , F2  e o número
2
a tal que 0  a  c . Chama-se hipérbole a curva do plano formada pelos pontos P do plano
que satisfazem a relação
Definição. Sejam F1 e F2 pontos distintos do plano cartesiano, c 
d ( P, F1 )  d  P, F2   2a
(6)
Os pontos F1 e F2 são chamados de focos da hipérbole e as distâncias r1  d  P, F1  e
r2  d  P, F2  de raios focais do ponto P. A reta que contém os focos recebe o nome de
eixo focal. O ponto médio entre F1 e F2 é chamado de centro da hipérbole. O número c é
a distância focal da hipérbole, ou seja, a distância de cada um dos focos ao centro. A reta
perpendicular ao eixo focal passando pelo centro é chamada de eixo normal. Os pontos da
hipérbole sobre o eixo focal são chamados de vértices.
Note que a equação (6) é equivalente a
d ( P, F1 )  d  P, F2    2a
No caso positivo, a distância de P ao foco F1 é maior que a de P ao foco F2 :
d ( P, F1 )  d  P, F2   2a  d  P, F2 
(7)
No caso negativo verifica-se o contrário, a distância de P ao foco F2 é maior que a de P ao
foco F1 :
d ( P, F2 )  d  P, F1   2a  d  P, F1 
(8)
Um ponto P não pode satisfazer simultaneamente estas duas desigualdades. Isso significa
que a hipérbole é formada por dois conjuntos disjuntos de pontos como mostra a figura 2.
Estes são chamados de ramos da hipérbole. Os pontos sobre o ramo da direita (esquerda)
satisfazem a desigualdade (7) ((8)). A figura 2 mostra o caso especial de uma hipérbole em
que os eixos focal e normal coincidem com os eixos cartesianos OX e OY ,
respectivamente.
Figura 2
A equação canônica da hipérbole
Considere a hipérbole cujo eixo focal coincide com o eixo OX , o eixo normal coincide
com o eixo OY , o centro C coincide com a origem O(0, 0) dos eixos de coordenadas, os
focos tem coordenadas F1 (c,0) e F2 (c,0) , c  0 . Seja P( x, y) ponto da hipérbole.
Usando a fórmula da distância, a relação (6) pode ser expressa como
 x  c
2
 y2 
 x  c
2
 y 2   2a
Passando o segundo radical para o lado direito da igualdade e elevando ao quadrado ambos
os lados, obtemos:
cx  a 2  a
x  c 2  y 2
Em seguida, elevamos os membros desta última equação ao quadrado:
(c2  a 2 ) x2  a 2 y 2  a 2 (c2  a 2 )
Como c  a , defina
b2 x 2  a 2 y 2  a 2b2 ,
ou ainda,
√
. Segue, então,
x2 y 2

1 ,
a 2 b2
(9)
A equação (9) é chamada de equação canônica e a relação
fundamental da hipérbole.
, relação
Observações
1. A equação da hipérbole é uma equação do segundo grau nas variáveis x e y .
2. Tomando y  0 na equação (9) obtemos que x   a . Portanto, V1  a, 0  e V2  a, 0 
são as coordenadas dos vértices da hipérbole sobre o eixo OX e 2a é a distância entre
eles. A equação não tem solução para x  0 significando isto que a hipérbole não tem
pontos sobre o eixo OY .
3. Todo ponto  x, y  tem abcissa x  a ou x  a . Dessa forma, a hipérbole é formada
pelo par de curvas situadas uma à direita e a outra à esquerda das retas x  a e x  a
tendo em comum com estas apenas os vértices. Ao contrário da elipse, a hipérbole não é
uma curva limitada. De fato, da equação segue
 y2 
x 2  a 2 1  2   a 2
 b 
4. Pela equação, se P( x, y) é ponto da hipérbole então o ponto Q( x, y) , simétrico a P
em relação ao eixo OY , o ponto R( x,  y) , simétrico a P em relação ao eixo OX , e o
ponto S ( x,  y) , simétrico a P em relação à origem, também são pontos da mesma
hipérbole. Portanto, a hipérbole é simétrica em relação aos eixos OX , OY e à sua
origem. Segue-se daí que a hipérbole é simétrica em relação aos seus eixos focal e
normal e, também, em relação ao seu centro.
Exemplo. Determine as coordenadas dos vértices e focos da hipérbole cuja equação
canônica é
x2 y 2

1
64 36
Solução. Comparando esta equação com a equação canônica geral (9), temos a  8 e b  6 .
Portanto, os seus vértices são: V1  8,0  e V2  8,0  . Pela relação c2  b2  a 2 obtemos
c  10 . Assim, os focos estão nos pontos F1 (10,0) e F2 (10,0) .
Retângulo fundamental
O retângulo ABCD de lados 2a e 2b mostrado na Figura 6.9 e tangente à hipérbole nos
seus vértices é chamado de retângulo fundamental da hipérbole. A denominação “eixos da
hipérbole” é aplicada aos segmentos de comprimento 2a e 2b que ligam os pontos médios
dos lados opostos do retângulo fundamental. O segmento 2b é também chamado de eixo
transverso ou normal. Como, pela relação fundamental da hipérbole, c 2  a 2  b 2 , o
b
comprimento da diagonal do retângulo fundamental é 2c . Além disso, a razão
,
a
coeficiente angular da diagonal, caracteriza sua forma. Quanto menor esta razão, mais
alongado ou “achatado” é o retângulo relativamente ao eixo OX e, por conseguinte, a
hipérbole.
Figura 3
Obs. Na Figura 3, desconsidere as retas
e
.
Assíntotas da hipérbole
b
b
x e s2 : y   x são chamadas de retas assíntotas da hipérbole. Observe
a
a
que as diagonais do retângulo fundamental estão sobre as assíntotas. Em especial, no caso
a  b , as assíntotas são perpendiculares entre si. A hipérbole, nesse caso, é chamada de
equilátera.
As retas s1 : y 
Teorema. As assíntotas não interceptam a hipérbole.
)
Demonstração: Consideremos a assíntota . Suponha que exista um ponto (
e que também pertence à hipérbole. Então as coordenadas de Q devem satisfazer a equação
da reta , isto é,
b
y0  x0
a
e, também, a equação da hipérbole
x0 2 y0 2

1
a 2 b2
Destas duas relações segue um absurdo, pois teríamos
2
x 2 y 2 x 2 1  bx 
1  02  02  02  2   0   0
a
b
a
b  a 
Isso significa que não pode existir um ponto comum à hipérbole e à assíntota
vale para .
. O mesmo
Há pontos da hipérbole tão próximos de uma assíntota quanto desejarmos mas as assíntotas
jamais interceptam a hipérbole.
Excentricidade da hipérbole
c
é chamado de
a
excentricidade da hipérbole. Como c  a , temos   1 . Lembrando que c 2  a 2  b 2 ,
obtém-se
Dada uma hipérbole com a equação (10) e distancia focal c , o número  
b2
  1 2
a
(12)
b
a excentricidade também diminui; do contrário,
a
ela aumenta. Quanto menor (maior) esta razão, mais alongado ou “achatado” é o retângulo
fundamental na direção do eixo OX ( OY ) e, também, a hipérbole. Portanto, a
excentricidade mede o grau de “achatamento” da hipérbole. No caso da hipérbole, quanto
menos achatada em relação ao eixo
mais excêntrica ela é.
Note que diminuindo o valor da razão
Exercícios
1) Prove que se  x0 , y0  satisfaz a equação da hipérbole, então os pontos   x0 , y0  ,
 x0 ,  y0  , e   x0 ,  y0 
também a satisfazem. Portanto, a hipérbole é simétrica em
relação aos eixos coordenados e em relação à origem.
2) Determine a equação da hipérbole com focos sobre o eixo OY nos pontos F1  0, c  e
F2  0, c  , c  0 , e vértices V1  0, a  , V2  0, a  .
3) Determine os vértices, focos, e assíntotas das hipérboles:
a) 4 x2  9 y 2  36
b) x 2  4 y 2  4
c) 9 x2  16 y 2  144
d) 16 x2  25 y 2  400
e) 4 x2  49 y 2  196
4) Determine a equação da hipérbole com
a) vértices  3, 0  e focos  5, 0  .
3
.
2
c) focos  6, 0  e assíntotas 5 y  2 5x .
b) vértices  4, 0  e excentricidade
5) Uma hipérbole passa no ponto P e uma de suas assíntotas é a reta r . Determinar a
equação da hipérbole nos casos
a) P (6, 2) e r : 2 x  5 y  0 ,
b)
P (3,-1) e r : 2 x  3 2 y  0 .
6) Provar que a excentricidade de qualquer hipérbole equilátera (isto é, com
equação) é igual a 2 .
, na
7) Provar que uma reta qualquer paralela a uma assíntota de uma hipérbole intercepta a
curva num único ponto.