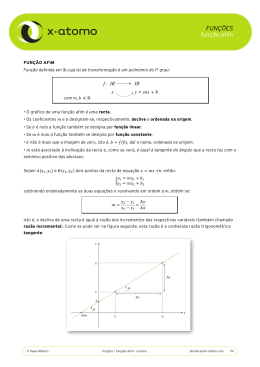
Introdução:
Esta apresentação refere-se à “Função afim como modelo da vida real”,
conteúdo de Matemática B. Pode ser utilizada por alunos para revisão mas
especialmente por professores. Tem como pré-requisitos todos os conceitos
relacionados com o conceito de função: domínio, contradomínio, objecto,
imagem, ... (provavelmente, estes conceitos terão que ser relembrados através
de exercícios, mas optei nesta apresentação por não o fazer).
Inicio esta apresentação pela definição de função afim, estudando depois
o seu comportamento. Depois de resolver um exemplo de utilização desta
função num contexto de vida real, deixo dois exercícios para serem resolvidos.
Acrescentar ainda, que esta apresentação foi pensada para 2 blocos de 90
minutos, tendo utilizado o livro referido no exemplo que deixo aqui e nos
exercícios que ficam para resolver. Os gráficos apresentados, foram todos
feitos utilizando o software Graph, que pode ser facilmente encontrado na
Internet.
A função afim como modelo de situações da vida real
Comecemos por relembrar:
Rectas:
 A expressão dada por:
trata-se duma recta horizontal paralela ao eixo dos xx.
Observação: As rectas verticais não representam uma função.
Antes de prosseguir e para os alunos: caso não se recordem do conceito de função,
consultem o manual do 8º ano de escolaridade.
 Uma função afim é uma função do tipo:
Portanto
A recta horizontal é um caso particular de função
afim. (m=0 ), aliás a função afim é uma recta.
Função afim
Estudo
Expressão
analítica
m é o declive da recta em relação ao eixo dos xx, b é a
ordenada na origem.
Fazendo b=0 temos:
m>0
m<0
Tal num caso como noutro, a função (recta) passa na origem. Continuando
com este exemplo: E se m for zero?
Função afim
Estudo (continuação)
m>0 (m=1)
b>0 (neste caso b=2)
Neste caso a função “sobe”,
sendo paralela à função y=x .
m<0 (m=-1)
b>0 (neste caso b=2)
Neste caso a função “sobe”, sendo
paralela à função y=-x.
y=x+2
y=-x+2
y=x
y=-x
O que acontecerá
se b<0?
Agora que em Portugal estamos com tanto frio é até apropriado.
Exemplo:
Às 08h00min a temperatura era de -5ºC e a relva do jardim estava coberta de
neve.
Com o decorrer do dia, à medida que a neve foi derretendo a temperatura
foi subindo, como se mostra no gráfico seguinte.
D
f
B
C
A
a. Defina, por uma expressão analítica, a função f. Calcule a temperatura às
17h00min.
b. A partir de que momento é que a temperatura é superior a 1ºC?
Observação: Apresente a resposta em horas e minutos.
Adaptado da página 10 do livro de Matemática B (parte 1) da Porto Editora 2005
Resolução
Queremos definir f por uma expressão analítica.
Ora, observando o gráfico de f vemos que temos
de definir a função por 3 ramos. Cada um destes
corresponde a um segmento de recta.
a)
Num caso e noutro, calculou-se a
equação reduzida da recta.
O segundo ramo é zero, pois o
declive é nulo (recta horizontal).
Declive de uma reta
O declive mede a inclinação de
uma recta face ao eixo dos xx.
Basta escolher dois pontos de
coordenadas A(x1,y1) e B(x2,y2) e
utilizar a seguinte fórmula :
55
5
x

, se 8  x  11
3
3

f ( x )  0, se 11  x  13
8
104
 x
, se 13  x  18
5
5
Terceiro ramo
da função
Resolução (cont):
b)
55
5
x

, se 8  x  11
3
3

f ( x )  0, se 11  x  13
8
104
 x
, se 13  x  18
5
5
Das funções representadas abaixo diga (Resolução):
Expressão analítica:
Domínio:
Contradomínio:
Zeros (se existirem): A função é nula
para x=0.
Expressão analítica:
Domínio:
Contradomínio:
Zeros (se existirem): Não tem.
g
f
Função quadrática
Expressão analítica:
Domínio:
Contradomínio:
Zeros (se existirem):
Mais tarde será estudada a
função quadrática, sendo
depois introduzida a
regressão quadrática.
h
Exercício 1
A Helena e o Pedro saíram de casa às 10hoo para um passeio de bicicleta, mas
optaram por caminhos diferentes, como está representado no gráfico abaixo.
Qual dos dois irmãos chegou primeiro a casa?
Represente por uma expressão analítica, as funções f e g.
Em que momento os dois irmãos estiveram à mesma distância de casa? Apresente
o resultado em horas e minutos.
Adaptado da página 24 do livro de Matemática B (parte 1) da Porto Editora 2005
Distância(km)
f
Pedro
Helena
g
Tempo (horas)
Exercício 2
O Tiago sai de casa às 8 horas. A uma velocidade constante de 10 km/h anda 15
minutos e, em seguida, pára durante igual período de tempo.
Regressa a casa a uma velocidade constante de 18 km/h.
Represente gráfica e analiticamente uma função que descreva esta viagem.
Adaptado da página 25 do livro de Matemática B (parte 1) da Porto Editora 2005
A seguir será introduzida a regressão linear,……………………