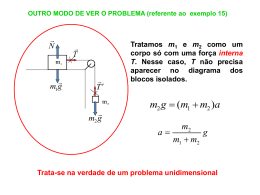
CENTRO MASSA
 Centro massa para um de sistema de 2 partículas
 Centro massa para várias partículas
 Centro de massa de corpos contínuos e uniformes
 Centro de massa e simetrias
CENTRO MASSA
Na mecânica existem várias situações em que se pode considerar a
massa de um corpo, ou mesmo de vários corpos, como se estivesse
concentrada em um único ponto. A esse ponto se dá o nome de
centro de massa.
CENTRO MASSA PARA UM DE SISTEMA DE 2 PARTÍCULAS
 ( ext ) F
12
F1

F21
 ( ext )
F2

 ( ext )
 d x1 
m1 2  F12  F1
dt

2
m d x2  F  F ( ext )
21
2
 2 dt 2
2
d 2x
(lembrar que a aceleração instantânea de uma partícula é a 
dt 2
)
3


 ( ext )  ( ext )
F
Distinguimos FORÇAS INTERNAS ( 21 e F12 ) das FORÇAS EXTERNAS (F
e F2
).
1
Somando-se as equações termo a termo:

2

 ( ext )  ( ext )
d x1
d x2 
m1 2  m2
 F12  F21  F1  F2
2
dt
dt


 ( ext )


d 2 x1
d 2 x2  ( ext )  ( ext )
 m1 2  m2 2  F1  F2   F
(porque F  F )
12
21
dt
dt
 (ext)
 F  é a força externa resultante. As forças internas se cancelam.
2
2
m1 x1  m2 x2   F (ext)
d 2 x1
d 2 x2
d
( ext )
m1 2  m2

F



dt
dt 2
dt2
Definimos:
xCM
m1 x1  m2 x2

m1  m2
Então:
F
( ext )
d 2 xCM
M
 MaCM
2
dt
onde M=m1+m2 é a massa total do sistema
4
O sistema se comporta como se toda massa estivesse concentrada no ponto xCM (centro
de massa) e a força externa agisse sobre ele.
xCM
( ext )
F

M
F
( ext )
d 2 xCM
M
dt 2
ou
( ext )
F
 MaCM

 é a 2a Lei de Newton para um sistema de 2 partículas
Em particular, se
F
( ext )
0
dxCM
 vCM  cte
dt
5
Exemplo 1. Calcular o centro de massa dos seguintes sistemas de duas partículas.
xCM
m1 x1  m2 x2

m1  m2
(a)
x1
x2
xCM
xCM
mx1  mx 2

2m
 xCM
x1  x2

2
(b)
x1
x2
 xCM
m1  m2
x
x
m1  m2
muito pequeno
xCM 
m1 x1  m2 x2 m1 x1

m1 m2
m1
muito pequeno
 xCM  x1
6
Exemplo 2
Exemplo 3
EXEMPLO 4
Centro de massa
9
No caso particular em que

F 0
d 2x
a 2 0
dt
dxCM
 vCM  cte.
dt
m = 80 kg
m = 60 kg
Exemplo 5. Dois patinadores no gelo (sem atrito
com o chão) encontram-se inicialmente a uma
distância de 12 m. Eles puxam as extremidades de
uma corda até se encontrarem. Em que ponto eles
se encontram? O resultado depende das forças
exercidas por eles?
Só há forças internas ao sistema  o centro de massa tem velocidade constante.
xCM 
m1 x1  m2 x2
m1  m2
 xCM 
0  80 kg  12 m  60 kg
m  5.1 m
80  60
Os patinadores se encontrarão a 5.1 m da posição inicial do patinador da esquerda.
O resultado não depende das forças exercidas por eles
uma vez que são forças internas
10
CENTRO DE MASSA PARA N PARTÍCULAS NUMA DIMENSÃO
xCM
m1 x1  m2 x2    mN xN
1


m1  m2    mN
M
N
m x
i 1
i i
CENTRO DE MASSA PARA N PARTÍCULAS EM TRÊS DIMENSÕES

rCM




m1r1  m2 r2  m3r3  ...mN rN

m1  m2  m3  ...mN
ou
 (ext)

 F  M aCM

1
rCM 
M

 mi ri
N
i 1
 é a 2ª lei de Newton para um sistema de partículas:
o sistema responde à resultante das forças externas como se a massa total M estivesse
toda concentrada no centro de massa.
11
Exemplo 6: Para o sistema de 3 partículas representado na figura, calcule a
posição do centro de massa do sistema abaixo:
m1  1 kg x1  0 m y1  0 m
m2  2 kg x2  0 m y2  3 m
m3  4 kg x3  4 m y3  0 m
0×1+ 0× 2 + 4× 4
m = 2,3 m
1+ 2 + 4
0×1+ 3× 2 + 0× 4
=
m = 0,9 m
1+ 2 + 4
x CM =
y CM
12
CENTRO DE MASSA DE CORPOS CONTÍNUOS E UNIFORMES
Se um corpo consiste de uma distribuição contínua de massa, podemos dividi-lo em porções
infinitesimais de massa dm e a soma transforma-se numa integral:
xCM
1

M
N
1
mi xi 
xdm


M
i 1
yCM
1

M
 ydm
zCM
1

M
 zdm
A massa infinitesimal dm pode pertencer a: um fio, uma superfície ou um volume:
dm =
 dl

: densidade linear de massa
 dA


: densidade superficial de massa
 dV
: densidade volumétrica de massa
Se o corpo (volume) tiver densidade uniforme:
xCM 

rCM
1
xdV

V
 
r  r dV



  r dV
1
y CM   ydV
V
M
dm   dV  dV :
V
1
z CM   zdV
V
Normalmente, não precisamos calcular estas integrais
triplas!
13
CENTRO DE MASSA E SIMETRIAS
Se um corpo tem um ponto, uma linha ou um plano de simetria, o centro de massa m
situa-se nesse ponto, linha ou plano.
Centro de simetria
Linhas de simetria
CM
CM
Planos de simetria
Lembrar que o centro de massa de um
corpo não é necessariamente um ponto
do corpo!
14
Exemplo 7
15