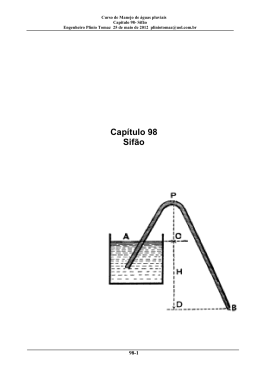
Sifão
Engenheiro Plínio Tomaz
Sifão normal e sifão invertido
Sifão normal
Sifão normal
Teorema de Bernouilli
• p/ γ + Z + V2/2g = constante se não houver perdas de cargas
• Mas existem perdas distribuídas hf e perdas
localizadas hs=∑Ks. V2/2g
• pA/ γ + ZA + VA2/2g = pF/ γ + ZF + VF2/2g + hfAF + hsAF
Esquema do sifão normal
Funcionamento: primeiro encher GF e dar a partida
Perda de carga unitária
Hazen-Willians
•
•
•
•
•
•
•
•
10,643 . Q 1,85
J = ----------------------C1,85 . D4,87
Sendo:
J= perda de carga em metro por metro (m/m);
Q= vazão em m3/s;
C= coeficiente de rugosidade da tubulação de Hazen-Willians;
D= diâmetro em metros.
• hf= J . L
Coeficiente C de Hazen-Willians
Material
Coeficiente de rugosidade C
Ferro fundido novo
130
Ferro fundido revestido com
cimento
130
Aço novo
120
Aço em uso
PVC
Ferro Fundido em uso
90
150
90
Perdas de cargas localizadas
hs=∑Ks. V2/2g
Válvula de pé com crivo até 60mm
Limite de sucção
Velocidades máximas na sucção
Exemplo
Funcionamento: primeiro encher GF e dar a partida
Dados do exemplo
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
Dimensionar o diâmetro do sifão de um barramento sendo:
Vazão= 26 L/s= 0,026 m3/s
Comprimento de sucção G até C= 25m
Comprimento total de GCF = 60m
Diferença de nível entre o ponto A e F = 5,00m
Material: PVC
C de Hazen-Willians= 100
Perdas localizadas em todo o trecho:
1 válvula de pé com crivo
2 curvas de 45
1 tê de saída lateral
1 registro de gaveta aberto
‘
Perdas localizadas na sucção:
1 válvula de pé com crivo
1 curvas de 45
1 tê de saída lateral
Exemplo
•
•
•
•
•
•
•
•
Primeiro
Vamos aplicar a equação de Bernouilli nos pontos A e F .
pA/ γ + ZA + VA2/2g = pF/ γ + ZF + VF2/2g + hfAF + Σks.VF2/2g
Sendo:
hf= perda de carga distribuida (m)
Σks.VF2/2g = perdas de cargas localizadas (m)
Exemplo
• pA/ γ + ZA + VA2/2g = pF/ γ + ZF + VF2/2g + hfAF + Σks.VF2/2g
• 0 + 5,0 + 0 = 0 + 0 + VF2/2g + hfAF + Σks.VF2/2g
•
5,0 = VF2/2g + LACF . 10,643 x Q 1,85/ (C 1,85 . D 4,87) +Σks.VF2/2g
•
• Mas V2/2g= 8.Q2/ (g.PI2 .D4 )
•
•
5,0 = 8.Q2/ (g.PI2 .D4 )+ LACF . 10,643 x Q 1,85/ (C 1,85 . D 4,87) +Σks.
8.Q2/ (g.PI2 .D4 )
•
Temos portanto uma equação em função do diâmetro D que
pode ser resolvido facilmente em planilha eletrônica por
tentativas.
•
Achamos: D=0,141m e V=1,67m/s < 1,80m/s OK ACE, 1992
• Fonte:
• Está no site www.pliniotomaz.com.br
• Complementos do livro Cálculos Hidrológicos
e Hidráulicos
• Engenheiro Plinio Tomaz
• E-mail: [email protected]