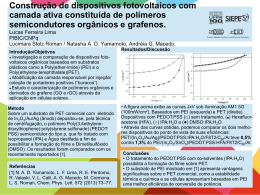
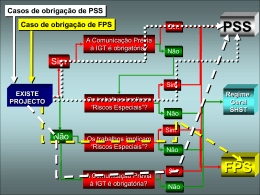
Definição de Parâmetros de “Power System
Stabilizers” para Melhoria do
Comportamento Dinâmico de Redes
Ângelo Mendonça
Orientador: Prof. João A. Peças Lopes
Mestrado em Engenharia
Electrotécnica e de Computadores
Origem do Problema

Em sistemas de energia de grande dimensão ou com características
longitudinais, a operarem próximo dos limites, surgem oscilações pouco
amortecidas de baixa frequência;

Essas oscilações caracterizam-se por estarem associadas à dinâmica do
rotor (modos electromecânicos) e dependerem do ponto de operação e não
do tipo ou local da perturbação -> modelos lineares;

Os PSS criam no gerador um binário amortecedor proporcional ao desvio
de velocidade, adicionando um sinal à referência do regulador de tensão;

Se ajustados correctamente dão uma importante contribuição para o
aumento do amortecimento das oscilações e melhoria da estabilidade.
Bloco de washout
VIN
sTW
1  sTW
Blocos delead-lag
1  sT1
1  sT2
1  sT3
1  sT4
LMAX
K
LMIN
VOTHSG
Formulação do Problema

Quais os melhores geradores para instalar PSS ?
•

Pretende-se identificar um número reduzido de PSS que permitam aumentar o
amortecimento dos modos de oscilação para os valores especificados.
Quais os parâmetros a adoptar ?
•
Pretende-se encontrar para cada PSS um conjunto de parâmetros que conduzam
ao aumento do amortecimento dos modos de oscilação de interesse em todos os
cenários de operação considerados – SOLUÇÃO ROBUSTA.

A resposta pode ser dada pela resolução de um problema de optimização em
que se procura a minimização das acções de controlo sujeita a que os limites
técnicos sejam respeitados e amortecimento seja superior ao especificado.

No entanto existem dificuldades de implementação: DIMENSÃO
Metodologia Desenvolvida

nc nm
min OF ( X )   (1  pij ) K i
Modelo Linear do SEE:
k 1 j 1 i 1
X  AX  Bu
Y  C X  Du

i   i  ji

i 
suj  i   min
K i. min  K i  K i. max
Ti. min  Ti  Ti. max
Modos de Oscilação:
det sI    A  0
 i

Em que:

Resolução:
 i 2  i 2
Factores de Participação:
p ji   ji ji 
n
i
a jj
•
•
•
•
•
•
pij – factor de participação ij;
Ki – é o ganho do PSS i;
n – número total de geradores;
Nm – número de modos;
nc – número de cenários.
Meta-Heurística (ex: EPSO Evolutionary Particle Swarm
Optimization)
Alguns Resultados e Conclusões
•
...
No futuro
•
Testar a metodologia com redes
de maior dimensão...
•
Comparar resultados com outros
métodos... Pior caso ...
•
...
0.002
Os parâmetros encontrados
conduzem a um aumento
significativo do amortecimento
em todos os cenários de operação
considerados...
SPEED DEVIATION (PU)
0
•
-0.002
A metodologia proposta identifica
correctamente os melhores locais
para instalar PSS...
0.002
•
SPEED DEVIATION (PU)
0

Conclusões
-0.002
