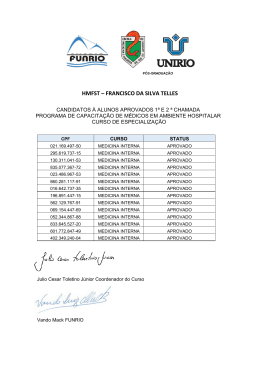
Matemática Elementar III – Progressões Aritméticas
7. Numa PA de n termos e razão r, temos a1= −
2/15, an = 2/3 e r . n = 1. Então, r e n valem,
respectivamente:
1. (MACK–SP) O trigésimo primeiro termo de uma
progressão aritmética de primeiro termo 2 e
razão 3 é:
a) 63;
b) 65;
c) 92;
d) 95;
c) −6;
d) −7;
c) 1/6 e 6;
d) 1/7 e 7;
8. (UFPA) Numa progressão aritmética, temos
a7 = 5 e a15 = 61. Então, a razão pertence ao
intervalo:
2. (FEI–SP) A razão de uma PA de 10 termos, cujo
primeiro termo é 42 e o último é –12, vale:
b) −9;
b) 1/3 e 3;
e) 1/9 e 9.
e) 98.
a) −5;
a) 1/5 e 5;
a) [8,10];
b) [6,8[;
c) [4,6[;
d) [2,4[;
e) [0,2[.
9. A razão de uma PA, na qual a3 + a5 = 20 e
a4 + a7 = 29, vale:
e) 0.
3. O termo geral de uma PA é dado por an = 2n – 1.
Então, o terceiro termo da PA vale:
a) 2;
b) 3;
c) 5;
d) 6;
c) −290;
d) −205;
c) 7;
d) 9;
10. (FGV–SP) A soma do 4.º e 8.º termos de PA é
20; o 31.º termo é o dobro do 16.º termo.
Determine a PA:
4. (MACK–SP) O produto das raízes da equação
x² + 2x − 3 = 0 é a razão de uma PA de
primeiro termo 7. O 100.o termo dessa PA é:
b) −304;
b) 5;
e) 11.
e) 4.
a) −200;
a) 3;
a) (−5, −2, 1, ...)
b) (5, 6, 7, ...)
c) (0, 2, 4, ...)
d) (0, 3, 6, 9, ...)
e) −191.
e) (1, 3, 5, ...)
5. (PUC–PR) Se em uma PA de 7 termos, de
razão K, retirarmos o segundo, terceiro, quinto
e sexto termos, a sucessão restante é uma PA
de razão:
11. A soma do 2.º e do 4.º termos de uma PA é 15
e a soma do 5.º e 6.º termos é 25. Então, o 1.º
termo e a razão valem respectivamente:
a) k;
b) 2k;
a) 7/3 e 3;
b) 7/4 e 4;
c) k/2;
d) 3k;
c) 7/2 e 2;
d) 7/5 e 5;
e) 7/6 e 6.
e) 5k.
12. (PUC–PR) Calculando o número de termos de
uma PA, onde o primeiro termo é 0,5 , o último
termo é 45,5 e a razão é 1,5, obtém-se:
6. O número de termos n de uma PA finita, cujo
primeiro termo é 1, o último 17 e cuja razão é r
= n − 1, vale:
a) 4;
b) 5;
a) 45;
b) 38;
c) 7;
d) 8;
c) 43;
d) 31;
e) 57.
e) 12.
87