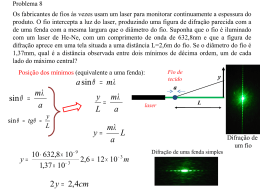
Interferência e Difração





Interferência em filmes finos
Duas fontes de luz
Difração
Fasores e Múltiplas fendas
Hologramas
FGE 160- 2o semestre 2007
Interferência em Filmes Finos
Diferença de fase:

r

2 
r

360
2t
  360  180
´
Onde, λ´=λ/n

2t
360
´
Interferência em Filmes Finos
Vidros ultra-planos
Vidros usuais
Franjas:
2t  m
t x
}
m 2

x

Duas fontes coerentes

Máximos de interferência:
d sin 

360
d sin   m
Onde, m=0, 1, 2, ...
Mínimos:
d sin   (m  1/ 2)
Duas fontes coerentes
m-ésimo máximo:
Amplitude:
ym  Ltg
E1  A0 sin(t )
tg
E  2 A0 cos( / 2)sin(t   / 2)
sin  
L
ym 
m
d
E2  A0 sin(t   )
Amplitude  2 A0 cos( / 2)
Intensidade:
I  4I0 cos2 ( / 2)
Espelho de Lloyd
Difração em uma fenda
Mínimos:
p/
a sin   m
m= 1, 2, 3, ...
p/ m=0 é um máximo.

r

360
ymin1 
L
a
Difração
Difração em uma fenda
Figura de difração com a interferência
entre duas fendas
m-ésimo máximo:
Sendo d > a
L
ymin1 
a
L
ym 
m
d
Fasores e Múltiplas Fendas
E1  A1 sin(t  1 )
E2  A2 sin(t   2 )
E  A sin(t   )
Representação com fasores
Fasores e Múltiplas Fendas
Três fendas
E1  A0 sin( )
E2  A0 sin(   )
E3  A0 sin(  2 )
Condição de mínimo

2

d sin  
2 yL
 d
Fasores e Múltiplas Fendas
Quatro fendas
Fasores e Múltiplas Fendas
uma fenda
Hologramas