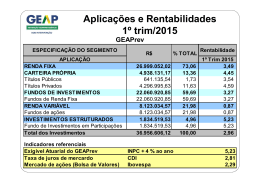
Funções
Profª. Lizlane Aparecida Trevelin
Disciplina: Matemática
E. E. Jesuíno de Arruda
São Carlos/SP
O conceito de função é
um dos mais
importantes em toda a
Matemática.
A idéia de função…
4° Trim.
3° Trim.
Leste
Oeste
Norte
2° Trim.
• Que faça corresponder a
todo elemento de
primeiro conjunto um
único elemento do
segundo , ocorre uma
função.
90
80
70
60
50
40
30
20
10
0
1° Trim.
• Toda vez que temos
dois conjuntos e
algum tipo de
associação entre eles.
Em nosso dia- a- dia temos
muitos exemplos de funções:
• o tempo de viagem é função, entre outras
coisas, da distância percorrida.
• a altura de uma criança é função de sua
idade;
• o consumo de combustível é função , entre
outras coisas , da velocidade.
• Perímetro de um triângulo é função da
medida de seus lados.
O conceito de função na
história...
• René Descartes ( 1596 - 1650) , filósofo e
matemático francês porpôs a utilização de
um sistema de eixos para localizar pontos e
representar graficamente as equações.
• Galileu Galilei ( 1564 - 1642) , astrônomo e
matemático italiano iniciou o método
experimental a partir do qual se pode
estabelecer uma lei que descreve relações
entre as variavéis de um fenômeno.
• Jean Bernonilli ( 1667 - 1748)
matemático suíço precursor do
conceito de função
• Peter G. Lejeune Dirichlet ( 1805 1859)matemático alemão estabeleceu o
conceito de função tal qual o
conhecemos hoje.
A função é um modo especial
de relacionar grandezas.
• duas grandezas x e y se relacionam de tal
forma que :
• x pode assumir qualquer valor em um
conjunto A dado.
• a cada valor de x corresponde um único
valor y em um dado conjunto B.
• os valores que y assume dependem dos
valores assumidos por x.
Temos várias maneiras para
representar a idéia de função.
Como representar uma função
diagrama de setas
gráficos
(plano cartesiano)
lei de formação
Representação gráfica
• No dia a dia
utilizamos esse
tipo de
representação em
vários setores .
Temos funções especiais
tais como:
Funções
função do primeiro grau
função do segundo grau
o gráfico é uma reta
o gráfico é uma parábola
que pode ser
crescente
decrescente
com concavidade para cima
com concavidade para baixo
E isso é só o
começo...
• Estaremos estudando funções por um
bom tempo.
•
Estaremos calculando e construindo
seus gráficos.
Espero que tenham
gostado...