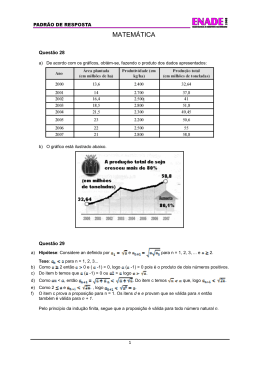
Aplicando o Conceito de Semelhança
Antônio J. R. Feitosa1, Jailton da S. Nascimento2 e John Wayne J. Costa3
Considere um paralelogramo ABCD de área 24 cm2, conforme figura abaixo, onde E e F são pontos médios dos lados
AB e BC, respectivamente, AC é uma diagonal do paralelogramo. Calcule a área do quadrilátero EFGH.
Fig. 1
Solução: Método, calcular as áreas que não estão coloridas e subtrair da área do paralelogramo. Antes de realizar
qualquer cálculo, vamos relembra alguns conceitos.
Primeira: A razão entre áreas de figuras semelhantes é igual a razão de semelhança ao quadrado.
Segundo: Dois triângulos com a mesma e a mesma base tem áreas congruentes.
Observe na fig. 1 que os triângulos ABC e AEF são semelhantes com razão de semelhança igual a 2, pois,
𝐵𝐴 𝐵𝐶 𝐴𝐶
=
=
=2
𝐵𝐸 𝐵𝐹 𝐸𝐹
Por que E e F são pontos médios de BA e BC. Como a área do paralelogramo é 24 cm2 então a área do triângulo ABC
é 12 cm2, portanto, a área do Triângulo BFE é 1/4 da área do triângulo BAC, isto é, 3 cm3.
Fig. 2
Na fig. 2, h é a altura do paralelogramo ABCD e é também a altura do triângulo FCD, então temos que a área do
triângulo FCD
𝐵𝐶
∙ ℎ 𝐶𝐵 ∙ ℎ 24
Á𝑟𝑒𝑎(𝐹𝐶𝐷) = 2
=
=
= 6 𝑐𝑚2
2
4
4
De maneira semelhante, calculamos a área do triângulo EAD, tendo que sua altura em relação à base AD é h/2, assim
Á𝑟𝑒𝑎(𝐸𝐴𝐷) = 6 𝑐𝑚2
Falta, portanto, calcular a área HGD. Vamos observar que os triângulos AGD e FGC são semelhantes pelo caso AAA,
pois o ângulo 𝐴𝐺̂ 𝐷 e 𝐹𝐺̂ 𝐶 são oposto pelo vértice, e ângulo 𝜏 é congruente ao ângulo 𝛽 porque são ângulos alternos
internos forma duas paralelas cortadas por uma transversal, de maneira semelhante concluímos que os 𝛼 e 𝛾 são
congruentes, logo os lados são proporcionais, isto é,
ℎ1 ̅̅̅̅
𝐴𝐷
=
ℎ2 ̅̅̅̅
𝐵𝐶
2
̅̅̅̅ = 𝐵𝐶
̅̅̅̅ , porque são lados de um paralelogramo. Então,
Mas 𝐴𝐷
ℎ1
= 2 ↔ ℎ1 = 2 ∙ ℎ2
ℎ2
Então ℎ = 2 ∙ ℎ2 + ℎ2 = 3 ∙ ℎ2 ,
Vamos calcular a área do triângulo FGC,
𝐵𝐶 ℎ
𝐵𝐶
∙
∙ ℎ2
𝐵𝐶 ∙ ℎ 24
2
𝐴𝑟𝑒𝑎(𝐹𝐺𝐶) =
= 2 3=
=
=2
2
2
12
12
Assim temos, que a Á𝑟𝑒𝑎(𝐺𝐶𝐷) = 4.
Vamos calcular a área do triângulo EHA, para isto procedemos de maneira semelhante, considerando a altura do
retângulo com relação à base BA.
̅ = ℎ, ̅𝐼𝐻
̅̅̅ = ℎ2 e ̅𝐻𝐽
̅̅̅ = ℎ1 . Agora observe que o triângulo AEH é semelhante ao triângulo HCD pelo caso AAA.
𝐼𝐽
Fazendo os mesmos cálculos que fizemos na etapa anterior obtemos h1 = h/3 e daí concluímos que a área do triângulo
AEH é 2 cm2. Então o triângulo AGD tem área 8 cm2 e, portanto, a área do triangulo AHD é 4 cm2. Como a área do
triângulo ACD é 12 cm2 e Aárea(GCD) + Aárea(AHD) = 8 cm2, então a Aárea(DHG) = 4 cm2. Então a área do quadrilátero
EFGH é 5 cm2. Já observamos que os triângulos AHD, HGD e GCD têm a mesma altura relativa ao vértice D e também
têm a mesma área. Quando dois ou mais triângulos tem a mesma altura suas áreas são proporcionais às bases, então,
̅̅̅̅
4
𝐴á𝑟𝑒𝑎 (𝐴𝐻𝐷) 𝐴á𝑟𝑒𝑎 (𝐻𝐺𝐷) ̅̅̅̅
𝐴𝐻 𝐻𝐺
=1=
=
=
=
̅̅̅̅ ̅̅̅̅
4
𝐴á𝑟𝑒𝑎 (𝐻𝐺𝐷) 𝐴á𝑟𝑒𝑎 (𝐺𝐶𝐷) 𝐻𝐺
𝐺𝐶
Logo ̅̅̅̅
𝐴𝐻 = ̅̅̅̅
𝐻𝐺 = ̅̅̅̅
𝐺𝐶 .
Observe que os triângulos FGC e AHE têm a mesma área, mas não são congruentes.
1
Coordenador PIBID Matemática, 2 Bolsista PIBID, 3 Aluno Ensino médio da EEEM Olivina Olivia J. Pessoa PB