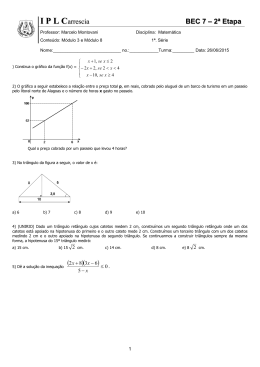
0
Resolução do problema 3 com cálculo diferencial
• Escolha de um referencial adaptado
A = (0, 0),
B = (x, 0)
• variável : x = AB = abcissa do ponto B.
• Altura do triângulo :
Como a área é conhecida e igual a 50, e como a área de um triângulo é igual
a 12 (base x altura), deduzimos que:
altura = h =
100
x
• Soma dos comprimentos dos dois catetos :
S(x) = AB + AC = x +
100
x
• Cálculo da derivada S 0 (x) :
S 0 (x) = 1 −
100
x2
• Cálculo dos zeros da derivada :
S 0 (x) = 1 −
100
=0
x2
⇔
x = 10
O triângulo rectânConclusão:
gulo de área igual a 50 cm2 , em que a soma dos dois catetos é mínima, é aquele
que é isósceles com comprimento dos catetos ambos iguais a 10 cm.