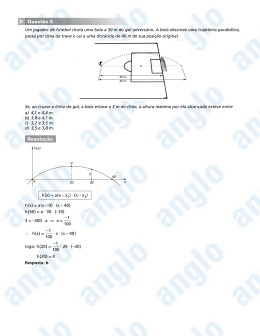
Interbits – SuperPro ® Web
MATEMÁTICA – XIV
FUNÇÕES E EQUAÇÕES DE 2º GRAU
NÚMEROS COMPLEXOS
1. (Ufpb 2011) – Em uma partida de futebol, um jogador, estando na lateral do campo, cruzou a
bola para um companheiro de equipe o qual se encontrava na lateral oposta, a uma distância
de 64 m. A bola passou 1,20 m acima da cabeça de um jogador, com 1,80 m de altura, da
equipe adversária, o qual, nesse instante, estava a 4 m de distância do jogador que realizou o
cruzamento, conforme figura abaixo.
Nessa situação, a bola descreveu uma trajetória em forma de arco de parábola até tocar o
gramado, quando foi dominada pelo companheiro de equipe.
Com base nessas informações, é correto afirmar que, durante o cruzamento, a bola atinge, no
máximo, uma altura de:
a) 12,8 m
b) 12 m
c) 11,2 m
d) 10,4 m
e) 9,6 m
2. (Upe 2011) – Se o valor mínimo de
5x2  6x  m é estritamente maior que 3, então é correto
afirmar que necessariamente
a) m>4
b) m>5
c) m<4
d) m<5
e) 4<m<5
3. (Fei 1994) – Escrevendo o número complexo z = 1/(1 - i) + 1/(1 + i) na forma algébrica
obtemos:
a) 1 - i
b) i - 1
c) 1 + i
d) i
e) 1
4. (Uel 1994) – A forma algébrica do número complexo z = (1 + 3i)/(2 - i) é
a) 1/2 - 3i
b) 5/3 + (7i/3)
c) -1/5 + (7i/5)
d) -1/5 + 7i
e) 3/5 + (4i/5)
Página 1 de 2
Interbits – SuperPro ® Web
Gabarito:
Resposta da questão 1:
[A]
Considerando o sistema cartesiano na figura acima, temos a função do segundo grau fatorada:
h(x) = a(x – 32).(x + 32) e o ponto ( -28,2)
3 = a.(-28 – 32).(-28 + 32)  a  
Portanto h(x) = 
1
80
1
.(x - 32).(x + 32)
80
A altura máxima será quando x for zero.
Portanto h(0) = 
1
.(0 - 32).(0 + 32) = 12,8m
80
Resposta da questão 2:
[A]

 ((6) 2  4.5.m)
20m  36
3
3
 3  20m  96  m  4,8
4.a
4.5
20
Portanto, a resposta A é a mais adequada.
Resposta da questão 3:
[E]
Resposta da questão 4:
[C]
Página 2 de 2