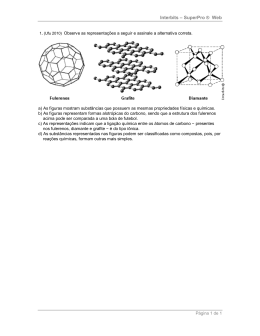
Interbits – SuperPro ® Web
MATEMÁTICA – XVI
GEOMETRIA PLANA – FUNÇÃO QUADRÁTICA
1. (Uesc 2011) – No período que precede o Natal, o comércio faz muitas promoções visando
incrementar suas vendas e, com esse objetivo, uma loja de departamentos fez uma promoção
de determinados produtos, vendendo todos a um mesmo preço unitário. Além disso, a cada n
unidades adquiridas, n  60 , o cliente teria n% de desconto, e, a partir dessa quantidade, ele
teria um desconto máximo de 60% . Um cliente comprou x unidades de produtos nessa
promoção e, ao calcular o valor V a ser pago, constatou que, dentro da faixa das 60 unidades,
poderia comprar mais produtos pagando o mesmo valor V.
De acordo com essas informações, pode-se concluir que x pertence ao intervalo
a) 10,19
b)  20,29
c) 30,39
d)  40,49
e) 50,59
2. (Ufpb 2011) – Em uma partida de futebol, um jogador, estando na lateral do campo, cruzou
a bola para um companheiro de equipe o qual se encontrava na lateral oposta, a uma distância
de 64 m. A bola passou 1,20 m acima da cabeça de um jogador, com 1,80 m de altura, da
equipe adversária, o qual, nesse instante, estava a 4 m de distância do jogador que realizou o
cruzamento, conforme figura abaixo.
Nessa situação, a bola descreveu uma trajetória em forma de arco de parábola até tocar o
gramado, quando foi dominada pelo companheiro de equipe.
Com base nessas informações, é correto afirmar que, durante o cruzamento, a bola atinge, no
máximo, uma altura de:
a) 12,8 m
b) 12 m
c) 11,2 m
d) 10,4 m
e) 9,6 m
Página 1 de 4
Interbits – SuperPro ® Web
3. (Ufpb 2011) – O Governo pretende construir armazéns com o intuito de estocar parte da
produção da safra de grãos, de modo que não haja desperdícios por situações adversas. A
seção transversal da cobertura de um desses armazéns tem a forma de um arco de
circunferência, apoiado em colunas de sustentação que estão sobre uma viga. O comprimento
dessa viga é de 24 m e o comprimento da maior coluna de sustentação é de 8 m, conforme
figura a seguir.
Considerando um sistema cartesiano de eixos ortogonais xy, com origem no ponto C, de modo
que o semieixo x positivo esteja na direção CD e o semieixo y positivo apontando para cima, é
correto afirmar que a equação da circunferência que contém o arco CD da seção transversal do
telhado, com relação ao sistema de eixos xy, é dada por:
2
2
a) (x −12) + (y + 5) = 169
2
2
b) (x −12) + (y − 7) = 193
2
2
c) (x −12) + (y − 6) = 180
2
2
d) (x −12) + (y + 6) = 180
2
2
e) (x −12) + (y − 5) = 169
4. (Cesgranrio 1991) – As retas r e s da figura são paralelas cortadas pela transversal t. Se o
ângulo B é o triplo de A, então B - A vale:
°
a) 90
°
b) 85
°
c) 80
°
d) 75
°
e) 60
5. (Cesgranrio 1990) – Duas retas paralelas são cortadas por uma transversal, de modo que a
°
soma de dois dos ângulos agudos formados vale 72 . Então, qualquer dos ângulos obtusos
formados mede:
°
a) 142 .
°
b) 144 .
°
c) 148 .
°
d) 150 .
°
e) 152 .
Página 2 de 4
Interbits – SuperPro ® Web
Gabarito:
Resposta da questão 1:
[D]
Seja p o preço unitário dos produtos, sem desconto. De acordo com o enunciado, o valor V a
ser pago pela aquisição de n produtos, com 0  n  60, n  , é dado pela função
p
V(n)  (100  n)%  n  p  
 (n2  100  n)
100
p

 [(n  50)2  2500]
100
p
 25  p 
 (n  50)2 .
100
Como a função V é quadrática e o eixo de simetria de seu gráfico é a reta n  50, segue que o
intervalo pedido é [40, 49].
Resposta da questão 2:
[A]
Considerando o sistema cartesiano na figura acima, temos a função do segundo grau fatorada:
h(x) = a(x – 32).(x + 32) e o ponto ( -28,2)
3 = a.(-28 – 32).(-28 + 32)  a  
Portanto h(x) = 
1
80
1
.(x - 32).(x + 32)
80
Página 3 de 4
Interbits – SuperPro ® Web
A altura máxima será quando x for zero.
Portanto h(0) = 
1
.(0 - 32).(0 + 32) = 12,8m
80
Resposta da questão 3:
[A]
Aplicando o teorema de Pitágoras no triângulo assinalado temos:
(R  8)2  122  R2  16R  208  R  13
Logo o centro é o ponto C(12,-5)
2
2
2
E a equação da circunferência (x – 12) + (y + 5) = 13
2
2
Ou seja, (x – 12) + ( y +5) = 169
Resposta da questão 4:
[A]
Resposta da questão 5:
[B]
Página 4 de 4