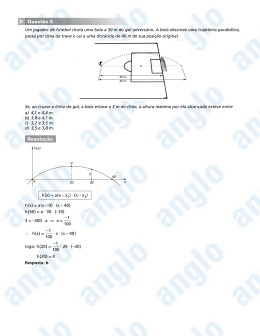
QUESTÃO 18 Uma bola é lançada do chão em um ângulo de 36,9° para dentro de uma quadra atrás de um muro de 5,0 m de altura e situado a 20 m de distância de quem a lançou. Desprezando-­‐
se a resistência do ar, e considerando a aceleração da gravidade, a velocidade inicial mínima para que a bola passe por cima do obstáculo e atinja a quadra, em m/s, é a) 12,5. b) 12,5 2. c) 12,5 3. d) 25 2. e) 25 3. RESOLUÇÃO: Considere a figura abaixo. A mínima velocidade de lançamento para que a bola passe por cima do muro é aquele em que a altura máxima atingida seja de 5,0. De acordo com a figura e o enunciado e usando trigonometria vamos separar os dados da questão. x = 20m y = 5,0m θ = 36,9° vy = v0 senθ vx = v0 cosθ O restante dos dados é obtido na tabela no início da prova de física. Como sabemos, no lançamento de um projétil os movimentos vertical e horizontal são estudados separadamente porque são independentes. Mas suas expressões podem ser associadas em determinados casos. No movimento vertical (direção y) temos 𝑔𝑡 !
𝑦 = 𝑣! 𝑡 −
2
onde t é o tempo que a bola leva para atingir o ponto mais alto da sua trajetória. Substituindo os dados na equação da altura máxima temos 10𝑡 !
𝑦 = 𝑣! 𝑠𝑒𝑛𝜃𝑡 −
2
5,0 = 𝑣! 0,60𝑡 − 5,0𝑡 ! (A) como temos duas incógnitas na expressão, vamos deixá-­‐la e resolver outra expressão. No movimento horizontal, temos 𝑥 = 𝑣! 𝑡 observe que o tempo que a bola leva para atingir o ponto mais alto é o mesmo que ela leva para percorrer os 20m. logo 𝑥 = 𝑣! 𝑐𝑜𝑠𝜃𝑡 𝑥
𝑡=
0,80𝑣!
!"
𝑡=
(B) !,!"!!
Substituindo a expressão B em A obtemos 20
20 !
5,0 = 𝑣! 0,60
− 5,0
0,80𝑣!
0,80𝑣!
2000
5,0 = 15 −
0,64𝑣!!
2000
10 =
0,64𝑣!!
Rearranjando a expressão e isolando a velocidade inicial, temos 𝑣! = !
200
0,64
𝑣! = 12,5√2 𝑚/𝑠 Questão resolvida pelo professor Otávio Nunes