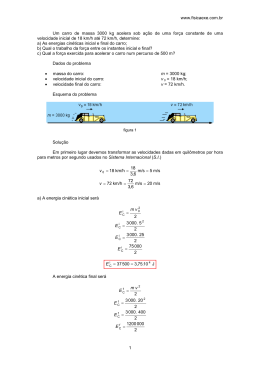
▼
Questão 54
Com relação à rampa de apoio, os corpos C1 e C2 estão em repouso e na iminência de movimento. Ao abandonar-se o conjunto, o corpo C1 sobe a rampa, com a qual existe atrito cinético de coeficiente μ = 0,2.
B
C2
1,60 m
A
C1
0,8 m
θ
Considerando-se os dados da tabela abaixo e fios e polias ideais, o ganho de energia cinética do corpo C2,
durante o deslocamento do corpo C1, do ponto A ao ponto B, é de
Massa do corpo C1 = 2,0 kg
Massa do corpo C2 = 2,0 kg
senθ = 0,80
cosθ = 0,60
→
| g | = 10 m/s2
a) 20 J
b) 2,0 J
c) 1,6 J
d) 0,80 J
e) 0,60 J
Resolução
Representando a situação descrita no enunciado, assinalando as forças aplicadas nos corpos e representando
as componentes pertinentes ao estudo do movimento do conjunto:
d
T2
B
T1
N1
C2
0,8 m
θ
C1
1,6 m
A
P2
d
0,8 m
A
P1
Colocando em destaque o deslocamento de C e utilizando a trigonometria:
d
0,8
0,8
= senθ
d
∴
d = 1m
θ
Como o trabalho da resultante é igual à soma do trabalho de todas as forças:
corpo C1: τR1 = τP1 + τA1 + τN1 + τT1
corpo C2:
τR2 = τP2 + τT2
Como a normal é perpendicular ao deslocamento, seu trabalho é nulo.
τR1 = τP1 + τA1 + τT1 (1)
τR2 = τP2 + τT2
(2)
τT1 = –τT2, temos:
τR1 + τR2 = τP1 + τP2 + τA
Somando (1) e (2) e sendo
Utilizando o teorema da energia cinética, o teorema da energia potencial e a definição de trabalho para obter
o trabalho do atrito, tem-se:
Δεc1 + Δεc2 = (m1 ⋅ g ⋅ hi – m1 ⋅ g ⋅ hf) + (m2 ⋅ g ⋅ hi – m2 ⋅ g ⋅ hf) + A ⋅ d ⋅ cosα
Sendo as massas e velocidades dos corpos 1 e 2 idênticas, as variações de energia cinética são iguais (Δεc1 = Δεc2).
2Δεc1 = (2 ⋅ 10 ⋅ 0,8 – 2 ⋅ 10 ⋅ 1,6) + (2 ⋅ 10 ⋅ 1 – 2 ⋅ 10 ⋅ 0) + μ ⋅ N ⋅ d ⋅ cosα
2Δεc1 = –16 + 20 + μ ⋅ (m2 ⋅ g ⋅ cosθ) ⋅ d ⋅ cosα
2Δεc = 4 + 0,2 ⋅ (2 ⋅ 10 ⋅ 0,6) ⋅ 1 ⋅ (–1)
∴
Δεc = 0,8 J
Resposta: d