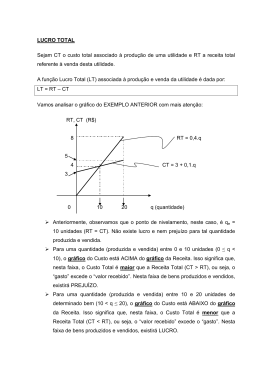
Matemática para
Negócios
Aula 7
André Brochi
Função Custo
total (CT)
Fornece o custo referente à
produção de uma certa
quantidade de determinado
bem.
Custo fixo: independe da quantidade produzida.
Por exemplo: aluguel, salários, etc.
Custo variável: depende da quantidade
produzida. Por exemplo: matéria-prima, mão de
obra, etc.
2
Função Receita
total (RT)
Determina o valor total recebido
(ou a receber) com a venda de
uma certa quantidade de bens
(ou serviços).
3
Equilíbrio da firma
Ponto de equilíbrio
de uma empresa
CT
RT
Elaborado pelo professor (Clipart)
Custo total = Receita total
Como determinar funções que
representem o custo e a receita?
4
Função Lucro
total (LT)
Determina a diferença entre a
receita obtida (ou a obter) com a
venda de uma certa quantidade
de bens (ou serviços) e o custo
de produção dos mesmos.
5
Aplicação 1
Uma impressora matricial é vendida por
R$ 200,00 a unidade. O custo fixo é de
R$ 1.600,00. O custo de produção de
cada impressora é de R$ 120,00.
a) Obtenha as funções custo total e receita total
para esse produto.
b) Determine, algébrica e graficamente, o ponto
de equilíbrio (ou de nivelamento).
c) Obtenha a função lucro total.
d) Determine a quantidade que deve ser
produzida e vendida para que o lucro seja de
R$ 5.040,00.
6
Denominaremos:
Q: quantidade produzida do produto;
CT: custo total;
CF: custo fixo;
CV: custo variável;
RT: receita total;
c: custo unitário de produção;
p: preço de venda.
7
a) Na aplicação 1, temos:
c = 120,00;
p = 200,00;
CF = 1.600,00.
Portanto:
CT = 1.600,00 + 120,00 · Q
e
RT = 200,00 · Q
8
b) Para determinar o ponto de equilíbrio
(nivelamento), devemos igualar a função
receita total à função custo total.
RT = CT
200 · Q = 1.600 + 120 · Q
200 · Q – 120 · Q = 1.600
80 · Q = 1.600
Q = 20 unidades
9
Se Q = 20, então:
RT = 200 · 20 = 4.000
CT = 1.600 + 120 · 20 = 4.000
Portanto, o ponto de equilíbrio é (20;4.000).
10
Gráfico
Ponto de nivelamento
RT
Ponto de
nivelamento
8000
7000
6000
5000
CT
4000
3000
2000
1000
0
0
4
8
12
16
20
Quantidade (Q)
Elaborado pelo professor
24
28
32
36
c)
LT = RT – CT
LT = 200Q – (1.600 + 120Q)
LT = 200Q – 1.600 – 120Q
LT = 80Q – 1.600
12
d)
LT = 5.040
80Q – 1.600 = 5.000
80Q = 6.640
Q = 83
13
De forma geral
CT = CF + CV , onde CV = cQ  CT = CF + cQ
RT = pQ
Ponto de equilíbrio (Qe)  RT = CT
p · Qe = CF + c·Qe
CF
Qe 
pc
14
Aplicação 2:
Uma empresa de refrigerantes apresenta
custo fixo de R$ 100.000,00, custo unitário
de R$ 0,60, e preço de mercado de R$ 2,00.
Sendo assim, monte as funções custo total e
receita total e encontre o ponto de equilíbrio
(Qe).
Custo total: CT = CF + CV = 100.000 + 0,6·Q
Receita total: RT = 2·Q
Ponto de equilíbrio: 100.000 + 0,6Q = 2Q
Q = 71.428,57
15
Valores das Funções
Q
CF = 100.000
CV = 0,6.Q
CT = CF + CV
RT = 2,00.Q
0
10.000
20.000
30.000
40.000
50.000
60.000
70.000
80.000
90.000
100.000
100.000
100.000
100.000
100.000
100.000
100.000
100.000
100.000
100.000
100.000
100.000
0
6.000
12.000
18.000
24.000
30.000
36.000
42.000
48.000
54.000
60.000
100.000
106.000
112.000
118.000
124.000
130.000
136.000
142.000
148.000
154.000
160.000
0
20.000
40.000
60.000
80.000
100.000
120.000
140.000
160.000
180.000
200.000
16
Gráfico
220.000
200.000
180.000
160.000
140.000
R$
120.000
Custo Total
100.000
Receita Total
80.000
60.000
40.000
20.000
0
Q
Elaborado pelo professor
Aplicação 3:
Uma indústria de autopeças tem um custo fixo
de R$ 15.000,00 por mês. Se cada peça
produzida tem um custo de R$ 6,00 e o preço
de venda é de R$ 10,00 por peça, quantas
peças a indústria deve produzir para ter um
lucro de R$ 30.000,00 por mês?
18
19
Bibliografia
DEMANA, Franklin et al. Pré-cálculo Vol. Único.
2ª Edição. Editora Pearson. São Paulo 2013.
IEZZI, Gelson et al. Fundamentos de
Matemática Elementar. Vol. 1 – Conjuntos e
Funções - Ed. Atual. São Paulo. 2013
SILVA, Sebasatião Medeiros da et al.
Matemática Básica para Cursos Superiores. Ed.
Atlas. São Paulo. 2002.
20
Matemática para
Negócios
Atividade 7
André Brochi
Atividade
Uma firma de serviços de fotocópias tem um
custo fixo de R$ 800,00 por mês e custos
variáveis de R$ 0,04 por folha que produz.
Expresse a função custo total em relação ao
número de páginas (Q) copiadas por mês. Se
os consumidores pagam R$ 0,09 por folha,
quantas folhas a firma tem que reproduzir
para não ter prejuízo?
22
23