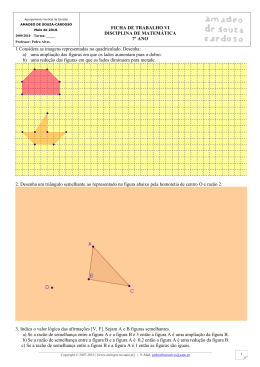
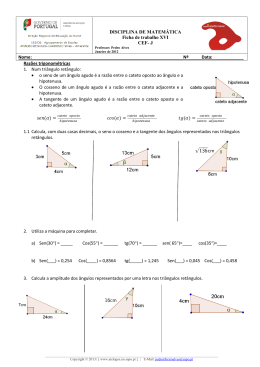
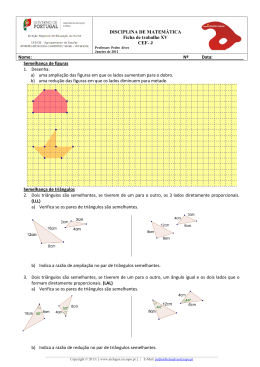
Agrupamento Vertical de Escolas
AMADEO DE SOUZA-CARDOSO
Maio de 2012.
2011/2012 Turma: _____
FICHA DE TRABALHO V
DISCIPLINA DE MATEMÁTICA
7º ANO
Professor: Pedro Alves.
1. Desenha:
a) uma ampliação das figuras em que os lados aumentam para o dobro.
b) uma redução das figuras em que os lados diminuem para metade.
2. Desenha um triângulo semelhante ao representado na figura abaixo pela homotetia de centro O e razão 2.
3. Indica o valor lógico das afirmações [V, F]. Sejam A e B figuras semelhantes.
a) Se a razão de semelhança entre a figura A e a figura B é 3 então a figura A é uma ampliação da figura B.
b) Se a razão de semelhança entre a figura A e a figura B é 0,2 então a figura B é uma redução da figura A.
c) Se a razão de semelhança entre a figura B e a figura A é 1 então as figuras são iguais.
___________________________________________________________________________________________________
Copyright © 2007-2012 | [www.atelogos.no.sapo.pt]. | E-Mail: [email protected]
1
4. Desenha um triângulo semelhante ao representado na figura abaixo pela homotetia de centro O e razão 0,5.
5. Considera as figuras representadas no quadriculado. Desenha
a) A imagem da figura à esquerda por uma homotetia de centro O e razão ½.
b) A imagem da figura à direita por uma homotetia de centro N e razão 3.
6. Indica o valor lógico das seguintes afirmações.
a)
b)
c)
d)
Existem figuras com os lados proporcionais que não são semelhantes.
Existem figuras com os ângulos correspondentes iguais que não são semelhantes.
Dois triângulos podem ter dois ângulos correspondentes iguais e não serem semelhantes.
Se os três lados de dois triângulos são proporcionais então os triângulos são semelhantes.
___________________________________________________________________________________________________
Copyright © 2007-2012 | [www.atelogos.no.sapo.pt]. | E-Mail: [email protected]
2
7. Considera os triângulos representados ao lado. A
unidade de comprimento na figura é o metro.
a)
b)
Mostra que os triângulos são semelhantes.
Copia e completa a tabela, justificando e apresentado
os valores arredondados às décimas.
Triângulo
AB = 2, 4
AC = 3, 9
BC = 3, 4
[ABC]
Triângulo
[FDE]
c) Indica, justificando, o valor lógico da afirmação. «O triângulo [FDE] é uma redução do triângulo [ABC] de
razão 1,6.»
8. Calcula a altura da árvore considerando os dados da
figura. Justifica a tua resposta.
9. Na figura está representada uma pirâmide quadrangular em
que o lado da base mede 40 metros. Às 16horas a sombra da
pirâmide media 33m enquanto que a sombra de uma vara de
2m media 3m como mostra a figura. Calcula a altura da
pirâmide.
10. Dois dos irmãos Dalton, que estavam um em frente do outro,
treinavam a pontaria com vista a um próximo assalto. De repente, o
Lucky Luke atirou-se para o chão e com um único tiro, furou os
dois chapéus inimigos. Supõe que:
 O Dalton mais alto tem 1,8 m de altura.
 A trajectória da bala foi rectilínea e que o Lucky Luke está a 8m
do Dalton mais baixo. E os dois irmãos Dalton estão separados por
1m.
Qual a altura do Dalton mais baixo? Explica a tua resposta
11. Os triângulos representados nas figuras são semelhantes? Justifica
a)
b)
.
12.
13. O Rui visitou um farol em forma de cilindro com um telhado em cone como
mostra a figura. O diâmetro da base do farol mede 8m. O Rui mede 1,65m e
observou que a sua sombra às 14horas era de 2m enquanto que a sombra do
farol media 16 m. Qual é a altura do farol? Justifica cuidadosamente a tua
resposta.
___________________________________________________________________________________________________
Copyright © 2007-2012 | [www.atelogos.no.sapo.pt]. | E-Mail: [email protected]
3
14. Um mapa está construído à escala de 1: 450000.
a) Sabe-se que a distância entre duas localidades é de 25km. A que distância estão representadas as
localidades no mapa?
b) Sabe-se que duas cidades estão representadas no mapa a uma distância de 1,4 cm. Qual é a distância
entre as duas cidades na realidade? Apresenta o resultado em km.
15. Na figura, representada ao lado, sabe-se que:
•


< ABC =
< EDC =
< ACE =
90 º
< BCA =
67 º
BC = 5m , AB = 12m , AC = 13m
CD = 6m

a) Calcula a amplitude dos ângulos internos dos dois triângulos e
justifica que são semelhantes.
b) Completa a tabela, indicando os cálculos auxiliares.
Triângulo [ABC]
AC = 13m
AB = 12m
BC = 5m
Triângulo [CDE]
16. Considera as figuras representadas no quadriculado.
a) Desenha a começar em P uma redução da figura F1 de razão 1 usando o método das quadriculas.
3
b) Desenha pelo método da homotetia de centro no ponto O uma ampliação de F2 de razão 3
17. Sabe-se que nos triângulos representados na figura:
• < ABD =
55º
• < ADB =
< BAC =
90º
• BD = 1,5m ; AC = 3, 6m e AB = 2, 6m .
a) Determina a amplitude dos ângulos < BAD , < DAC e < DCA .
b) Explica que o triângulo [BDA] é semelhante ao triângulo [CDA].
c) Calcula o comprimento AD , arredondado às décimas.
___________________________________________________________________________________________________
Copyright © 2007-2012 | [www.atelogos.no.sapo.pt]. | E-Mail: [email protected]
4