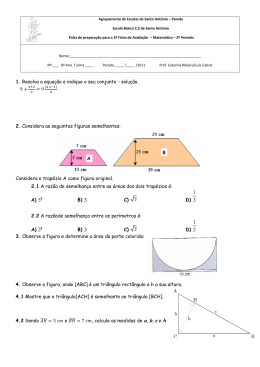
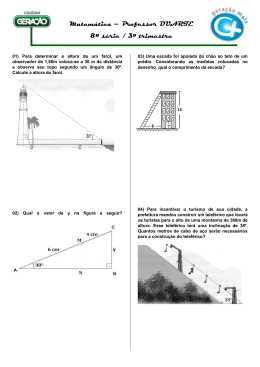
LISTA DE EXERCÍCIOS - 06
Goiânia, 26 de Agosto de 2014
Série: 3ª Série
 Turma: _____
Aluno(a):______________________________________________________________
Disciplina: Matemática  Professor: JR  e-mail: [email protected]
Semelhança de triângulos
ABC
*
~
 Â  M̂

 B̂  N̂

MNP  
Ĉ  P̂

 AB AC BC


k

 MN MP NP
2.
Determine o valor de x nos itens abaixo, sabendo que MN é
paralelo a BC.
O número real k é a razão de semelhança
3.
(UEG) Sobre o lado AB de um triângulo ABC, marca-se um ponto
D e por ele traça-se uma paralela ao lado BC, que determina sobre o
lado AC o ponto E. Sabendo-se que o lado AB mede 15 cm, que a
2
razão entre os segmentos AD e DB é
e que o segmento AE mede 8
3
cm, calcule o comprimento do segmento CE.
Se os triângulos ABC e MNP são semelhantes, então :
 AB AC BC
AH



k 
MG
 MN MP NP
 PerímetroABC
k

 PerímetroMNP
 Área ABC

 k2
 Área MNP
* Quando k = 1, os triângulos ABC e MNP são congruentes.
* Aplicações importantes (base média)
4.
(Unesp) Um obelisco de 12 m de altura projeta, num certo
momento, uma sombra de 4,8 m de extensão. Calcule a distância
máxima que uma pessoa de 1,80 m de altura poderá se afastar do
centro da base do obelisco, ao longo da sombra, para, em pé, continuar
totalmente na sombra.
5.
(UFG) Em um jogo de sinuca, uma bola é lançada do ponto O
para atingir o ponto C, passando pelos pontos A e B, seguindo a
trajetória indicada na figura abaixo.

Critérios de semelhança
Os critérios de semelhança são condições suficientes para
garantir a semelhança entre dois triângulos. São eles:
a) AA (~) – dois ângulos correspondentes (homólogos)
congruentes;
b) LLL (~) – os três lados homólogos proporcionais;
c) LAL (~) – dois lados homólogos proporcionais e o ângulo entre
os dois lados do primeiro triângulo congruente ao ângulo
correspondente do segundo triângulo.
Exercícios de Sala
1.
Determine o valor de x na figura abaixo:
Nessas condições, calcule:
a) o ângulo  em função do ângulo ;
b) o valor de x indicado na figura.
www.colegiopodium.com.br
RESPONSABILIDADE AMBIENTAL – Nossos papéis são de florestas 100% plantadas e renováveis
-1-
6.
Seja ABC um triângulo equilátero de lado 20 cm. Uma reta
passando pelo ponto médio M do lado AB corta o lado AC no ponto N
e o prolongamento do lado BC no ponto P, de tal modo que CP = 12
cm. Determine a razão entre CN e NA.
a)
a c  a
ab
abc
ab
e)
ac
b)
2b
2ab
d)
abc
Exercícios Propostos
1.
(UNESP) A figura representa uma chapa de alumínio de formato
triangular de massa 1 250 gramas. Deseja-se cortá-la por uma reta r
paralela ao lado BC e, que intercepta o lado AB em D e o lado AC
em E, de modo que o trapézio BCED tenha 700 gramas de massa. A
espessura e a densidade do material da chapa são uniformes.
Determine o valor percentual da razão de AD por AB . Dado:
c)
ab
bc
5.
(CEUB) O triângulo ABC tem base 18 cm e altura 12 cm. O
perímetro do quadrado inscrito nesse triângulo será:
11  3,32
a) 7,2 cm
b) 28,8 cm c) 14,4 cm d)
5
cm e) 3,6 cm
36
6.
a) 88,6.
b) 81,2.
c) 74,8.
d) 66,4.
e) 44,0.
2.
(Unicamp) Uma rampa de inclinação constante, como a que dá
acesso ao Palácio do Planalto em Brasília, tem 4 metros de altura na
sua parte mais alta. Uma pessoa, tendo começado a subi-la, nota que
após caminhar 12,3 metros sobre a rampa está a 1,5 metros de altura
em relação ao solo.
a) Faça uma figura ilustrativa da situação descrita.
b) Calcule quantos metros a pessoa ainda deve caminhar para
atingir o ponto mais alto da rampa.
3.
(FUVEST) Um teleférico transporta turistas entre os picos A e B
de dois morros. A altitude do pico A é de 500 m, a altitude do pico B é
de 800 m e a distância entre as retas verticais que passam por A e B é
de 900 m. Na figura, T representa o teleférico em um momento de sua
ascensão e x e y representam, respectivamente, os deslocamentos
horizontal e vertical do teleférico, em metros, até este momento.
(FGV) Quando duas resistências elétricas de valores R1 e R2 são
dispostas em paralelo (figura abaixo), o valor da resistência
R R
equivalente às duas primeiras é dado por R  1 2 .
R1  R2
A figura a seguir mostra duas semirretas AX e BY perpendiculares
à reta r. Na primeira foi marcado o ponto A', de forma que AA' = R1, e
na segunda foi marcado o ponto B', de forma que BB' = R2. As retas
A'B e AB' cortaram-se em P e foi traçado o segmento PP'
perpendicular a r.
Mostre que PP' é igual ao valor da resistência R.
Gabarito - Exercícios Propostos
a) Qual é o deslocamento horizontal do teleférico quando o seu
deslocamento vertical é igual a 20m?
b) Se o teleférico se desloca com velocidade constante de 1,5 m/s,
quanto tempo o teleférico gasta para ir do pico A ao pico B?
1.
2.
D
a)
3.
4.
5.
6.
a) 60 m
b) t  632,4 s
E
B
Demonstração
4.
(Canguru) Na figura, o triângulo retângulo tem lados a, b e c.
Qual é o valor do raio r da semicircunferência inscrita no triângulo,
como na figura?
b) 20,5 m
Goiânia-GO - Fone: 3088-0088 – www.colegiopodium.com.br
-2-