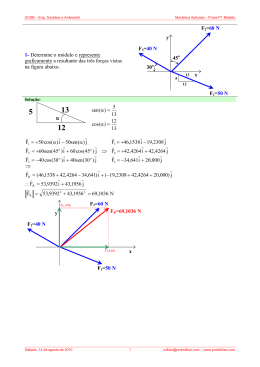
3.18 Os arames de aço AB e AC suportam a massa de 200 kg. Supondo que a tensão
normal admissível para eles seja σadm = 130 MPa, determinar o diâmetro requerido
para cada arame. Além disso, qual será o novo comprimento do arame AB depois que
a carga for aplicada? Supor o comprimento sem deformação de AB como sendo
750 mm. Eaço = 200 GPa.
y
FAB
FAC
60o
α
x
F
Solução:
5
4
α
3
∑F
∑F
4
= 0,8
5
3
cos(α) = = 0,6
5
sen (α) =
F = 200 × 9,80665 = 1961,33 N
x
= 0 ⇒ − FAB × cos(60 o ) + FAC × cos(α) = 0
y
= 0 ⇒ FAB × sen (60 o ) + FAC × sen (α) − F = 0
Resolvendo:
FAB = 1279,66 N
FAC = 1066,39 N
Assim, os diâmetros serão:
πd 2AB
F
1279,66
= AB =
⇒ d AB = 3,54 mm
4
σ adm
130
πd 2AC
F
1066,39
= AC =
⇒ d AC = 3,23 mm
4
σ adm
130
O deslocamento do arame AB será:
FAB L AB
1279,66 × 750
=
= 0,488 mm
2
πd AB
π × 3,54 2
200000 ×
E
4
4
Resposta: Os diâmetros requeridos para os arames AB e AC são 3,54 mm e 3,23 mm, respectivamente. O
novo comprimento do arame AB será de 750,488 mm.
δ=