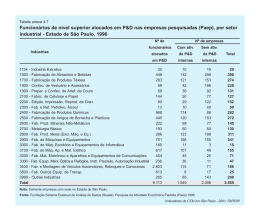
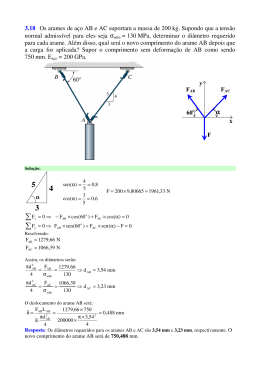
Questão 37
Um corpo parte do repouso em movimento
uniformemente acelerado. Sua posição em
função do tempo é registrada em uma fita a
cada segundo, a partir do primeiro ponto à
esquerda, que corresponde ao instante do início do movimento. A fita que melhor representa esse movimento é:
a)
a) 20N.
d) 5N.
b) 15N.
e) 2,5N.
c) 10N.
alternativa D
As forças que atuam sobre os blocos na direção
do movimento são dadas por:
FAB
F
A
fat.
B
FAB
fat.
Do Princípio Fundamental da Dinâmica, vem:
F − FAB − fat. = m γ
⇒
FAB − fat. = m γ
⇒ F − FAB − fat. = FAB − fat. ⇒
b)
⇒ 2 FAB = F ⇒ 2 FAB = 10 ⇒
FAB = 5 N
c)
Questão 39
d)
Ao se colocar um satélite em órbita circular
em torno da Terra, a escolha de sua velocidade v não pode ser feita independentemente do raio R da órbita. Se M é a massa da
Terra e G a constante universal de gravitação, v e R devem satisfazer a condição
e)
alternativa C
Considerando um MRUV, o espaçamento entre
dois intervalos iguais de tempo deve aumentar
continuamente, como indicado na alternativa C.
a) v2 R = GM.
v
c) 2 = GM.
R
e) vR = GM.
b) vR2 = GM.
v2
d)
= GM.
R
alternativa A
Questão 38
Dois blocos idênticos, A e B, se deslocam sobre uma mesa plana sob ação de uma força
de 10N, aplicada em A, conforme ilustrado na
figura.
Para um satélite em órbita circular em torno da
Terra temos:
mv 2
GmM
Rcp = Fgrav. ⇒
=
⇒ v 2 R = GM
R
R2
Questão 40
Se o movimento é uniformemente acelerado,
e considerando que o coeficiente de atrito cinético entre os blocos e a mesa é µ = 0,5, a
força que A exerce sobre B é:
Um bloco sobe uma rampa deslizando sem
atrito, em movimento uniformemente retardado, exclusivamente sob a ação da gravidade, conforme mostrado na figura.
física 19
Pode-se afirmar que a razão entre a energia
cinética final de B e a inicial de A é:
2m
m
M2
b)
.
c)
.
a) 2 .
M
2M
m
d)
Ele parte do solo no instante t = 0 e chega ao
ponto mais alto em 1,2 s. O módulo da velocidade em função do tempo é apresentado no
gráfico.
M
.
m
e)
m
.
M
alternativa E
Sendo o sistema formado pelos corpos A e B isolado, temos:
m
Qantes = Qdepois ⇒ mv A = Mv B ⇒ v B =
v
M A
A razão entre a energia cinética final de B e a inicial de A é dada por:
2
⎛m
⎞
Mv B2
⎜ v A⎟
B
⎠
EC
ECB
m
M ⎝M
= 22 =
⋅
=
⇒
A
2
M
m
EC
mv A
vA
ECA
2
Questão 42
Nos quadrinhos da tira, a mãe menciona as fases da água conforme a mudança das estações.
Considerando g = 10,0 m/s2 , a altura em que
o bloco se encontrava em t = 0,4 s era
a) 0,5 m.
b) 1,0 m.
c) 1,6 m.
d) 2,5 m.
e) 3,2 m.
alternativa B
Através do gráfico temos que, em t = 0,4 s, a velocidade do bloco é v = 4 m/s.
Adotando o referencial no solo, da conservação
de energia, vem:
mv 02
62
42
mv 2
=
+ mgh ⇒
=
+ 10h ⇒
2
2
2
2
⇒
h = 1,0 m
Questão 41
Um corpo A de massa m, movendo-se com
velocidade constante, colide frontalmente
com um corpo B, de massa M, inicialmente
em repouso. Após a colisão, unidimensional e
inelástica, o corpo A permanece em repouso e
B adquire uma velocidade desconhecida.
Entendendo “boneco de neve” como sendo
“boneco de gelo” e que com o termo “evaporou” a mãe se refira à transição água → va-
física 20
por, pode-se supor que ela imaginou a seqüência
gelo → água → vapor → água.
As mudanças de estado que ocorrem nessa
seqüência são
a) fusão, sublimação e condensação.
b) fusão, vaporização e condensação.
c) sublimação, vaporização e condensação.
d) condensação, vaporização e fusão.
e) fusão, vaporização e sublimação.
alternativa B
De acordo com a seqüência, temos:
gelo → água: fusão
água → vapor: vaporização
vapor → água: condensação
Questão 43
Um gás ideal é submetido às transformações
A → B, B → C, C → D e D → A, indicadas no
diagrama PxV apresentado na figura.
alternativa E
Analisando as afirmações, temos:
I. Correta. Para haver variação de energia interna
deve haver variação de temperatura. Como a
transformação A → B é isotérmica, não há variação de energia interna.
II. Correta. Ao compararmos duas isotermas em
um diagrama P × V, quanto mais próxima a isoterma se encontra do eixo V, menor é a sua temperatura.
III. Correta. Como a transformação D → A é isovolumétrica, não há trabalho realizado. Da 1ª Lei da
0
Termodinâmica, vem: Q = τ + ∆U ⇒ Q = ∆U
Questão 44
Considere as cinco posições de uma lente convergente, apresentadas na figura.
O
I
1
Com base nesse gráfico, analise as afirmações.
I. Durante a transformação A → B, a energia
interna se mantém inalterada.
II. A temperatura na transformação C → D é
menor do que a temperatura na transformação A → B.
III. Na transformação D → A, a variação de
energia interna é igual ao calor absorvido
pelo gás.
Dessas três afirmações, estão corretas:
a) I e II, apenas.
b) III, apenas.
c) I e III, apenas.
d) II e III, apenas.
e) I, II e III.
2
3
5
4
A única posição em que essa lente, se tiver a
distância focal adequada, poderia formar a
imagem real I do objeto O, indicados na figura, é a identificada pelo número
a) 1.
b) 2.
c) 3.
d) 4.
e) 5.
alternativa C
Pela propriedade do centro óptico, temos a figura:
O
I
1
2
3
4
5
Portanto a única posição da lente é a indicada
pela figura 3.
física 21
Fel. = P
Questão 45
Fel. = |q | ⋅ E
Uma pequena esfera suspensa por uma mola
executa movimento harmônico simples na direção vertical. Sempre que o comprimento da
mola é máximo, a esfera toca levemente a superfície de um líquido em um grande recipiente, gerando uma onda que se propaga com velocidade de 20,0 cm/s. Se a distância entre as
cristas da onda for 5,0 cm, a freqüência de oscilação da esfera será
a) 0,5 Hz.
b) 1,0 Hz.
c) 2,0 Hz.
d) 2,5 Hz.
e) 4,0 Hz.
alternativa E
A freqüência de oscilação da esfera é a mesma
da onda gerada no líquido.
Considerando que 5,0 cm é a distância entre duas
cristas sucessivas (λ = 5,0 cm), da equação fundamental da ondulatória, temos:
v = λ ⋅ f ⇒ 20,0 = 5,0 ⋅ f ⇒
f = 4,0 Hz
Uma gotícula de óleo com massa m e carga
elétrica q atravessa, sem sofrer qualquer deflexão, toda a região entre as placas paralelas
e horizontais de um capacitor polarizado,
como mostra a figura.
Se a distância entre as placas é L, a diferença
de potencial entre as placas é V e a aceleração da gravidade é g, é necessário que q/m
seja dada por
gV
VL
gL
a)
.
b)
.
c)
.
L
g
V
V
.
gL
e)
⇒ |q | ⋅
V
= mg ⇒
L
|q |
g ⋅L
=
m
V
⇒
Questão 47
Um circuito com 3 resistores iguais é submetido a uma diferença de potencial V entre os
pontos A e C, conforme mostra a figura.
A
B
R
V
R
R
C
Questão 46
d)
V
E =
L
P = mg
L
.
gV
alternativa C
Como temos um MRU, a força elétrica deve equilibrar a força peso. Assim, temos:
A diferença de potencial que se estabelece entre os pontos A e B é
V
V
V
2
3
.
b)
.
c)
.
d) V.
e) V.
a)
4
3
2
3
2
alternativa D
A resistência equivalente do circuito é R eq. = R +
R
3R
. Assim, a corrente que passa entre A
+
=
2
2
e B é dada por:
2V
V
V
i =
=
=
3R
3R
R eq.
2
Portanto, U AB é obtida de:
U AB = R ⋅ i = R ⋅
2V
⇒
3R
U AB =
2
V
3
Questão 48
Um dos lados de uma espira retangular rígida com massa m = 8,0 g, na qual circula uma
corrente I, é atado ao teto por dois fios não
condutores de comprimentos iguais. Sobre
esse lado da espira, medindo 20,0 cm, atua
física 22
um campo magnético uniforme de 0,05T, perpendicular ao plano da espira. O sentido do
campo magnético é representado por uma
seta vista por trás, penetrando o papel, conforme é ilustrado na figura.
Considerando g = 10,0 m/s2 , o menor valor
da corrente I que anula as trações nos fios é
a) 8,0 A.
b) 7,0 A.
c) 6,0 A.
d) 5,0 A.
e) 4,0 A.
alternativa A
Para que as trações sejam nulas e a corrente I
seja mínima, a força magnética deve equilibrar o
peso da espira. Assim, temos:
Fmag. = P
Fmag. = B ⋅ I ⋅ l ⇒ B ⋅ I ⋅ l = mg ⇒
P = mg
⇒ 0,05 ⋅ I ⋅ 20,0 ⋅ 10 −2 = 8,0 ⋅ 10 −3 ⋅ 10,0 ⇒
⇒
I = 8,0 A