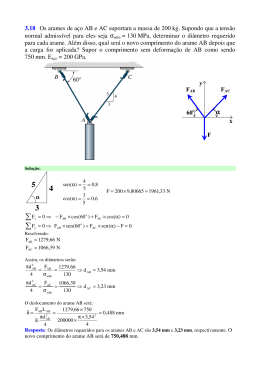
UCDB – Eng. Sanitária e Ambiental
Mecânica Aplicada – Prova P1 Modelo
F2=60 N
y
F3=40 N
1- Determine o módulo e represente
graficamente a resultante das três forças vistas
na figura abaixo.
45o
30o
13
5
x
12
F1=50 N
Solução:
5
13

12
5
13
12
cos() 
13
sen () 






F1  50 cos() i  50sen () j
F1  46,1538 i  19,2308 j






F2  60sen (45 o ) i  60 cos(45 o ) j  F2  42,4264 i  42,4264 j






F3  34,641i  20,000 j
F3  40 cos(30 o ) i  40sen (30 o ) j




FR  (46,1538  42,4264  34,641) i  (19,2308  42,4264  20,000) j



 FR  53,9392 i  43,1956 j

FR  53,9392 2  43,1956 2  69,1036 N
43,1956
y
F2=60 N
FR=69,1036 N
F3=40 N
53,9392
x
F1=50 N
Sábado, 14 de agosto de 2010
1
[email protected] – www.profwillian.com
UCDB – Eng. Sanitária e Ambiental
Mecânica Aplicada – Prova P1 Modelo
y
F1=75 N
F
2- Se as forças F1 e F2 são conhecidas,
determine a orientação  e o módulo da força F
de modo que o sistema de forças coplanares se
encontre em equilíbrio estático.
60o

x
F2=50 N
Solução:
 Fx  0  F  cos()  75  cos(60 o )  0  F 
75  cos(60 o )
cos()
F
(2)
y
 0  F  sen ()  75  sen (60 o )  50  0
(1)
(1) em (2)
75  cos(60 o )
 sen ()  75  sen (60 o )  50
cos()

tg() 
50  75  sen (60 o )
 0,398717
75  cos(60 o )
   21,738 o
75  cos(60 o )
cos(21,738 o )
 F  40,3709 N
F
Sábado, 14 de agosto de 2010
2
[email protected] – www.profwillian.com
UCDB – Eng. Sanitária e Ambiental
Mecânica Aplicada – Prova P1 Modelo
z
3- Encontre o módulo e os ângulos
diretores da força resultante entre F1
e F2.
Considere cada quadriculado 1 cm x
1 cm
B
F1=30 N
A
F2=50 N
O
y
C
x
Solução:
As coordenadas dos pontos são:
A(1, 0, 4)
B(0, 6, 5)
C(3, 8, 0)







rBA

(1  0) i  (0  6) j  (4  5)k
u BA   
 0,162221 i  0,973329 j  0,162221 k
rBA
12  6 2  12







rCA

(1  3) i  (0  8) j  (4  0)k
u CA   
 0,218218 i  0,872872 j  0,436436 k
rCA
2 2  82  4 2

F1 

F2 









 
F1 .u BA  30. 0,162221 i  0,973329 j  0,162221 k  4,86664 i  29,1999 j  4,86664 k






 
F2 .u CA  50.  0,218218 i  0,872872 j  0,436436 k  10,9109 i  43,6436 j  21,8218 k









 
FR  F1  F2  4,86664 i  29,1999 j  4,86664 k   10,9109 i  43,6436 j  21,8218 k

 






FR  6,04425 i  72,8434 j  16,9551 k

FR  6,04425 2  72,8434 2  16,95512  75,0345 N
F
  arc cos Rx
 FR


  arc cos  6,04425   94,6 o

 75,0345 

F
Ry
  arc cos 
 FR


  arc cos  72,8434   166,1o

 75,0345 

F
  arc cos Rz
 FR


  arc cos 16,9551   76,9 o

 75,0345 

Sábado, 14 de agosto de 2010
3
[email protected] – www.profwillian.com
UCDB – Eng. Sanitária e Ambiental
Mecânica Aplicada – Prova P1 Modelo
4- Encontre os
ângulos internos do
triângulo formado
pelos pontos A, B e
C vistos na figura
ao lado.
Solução:
As coordenadas dos pontos são:
A(1, 0, 4)
B(0, 6, 5)
C(3, 8, 0)




 


rAB  (0  1) i  (6  0) j  (5  4)k   i  6 j  k  rAB  6,16441








rAC  (3  1) i  (8  0) j  (0  4)k  2 i  8 j  4 k  rAC  9,16515
 
rAB .rAC  (1)  2  6  8  1  (4)  42
 
 rAB .rAC 
42


  arc cos 
  41,98 o
   arc cos
 6,16441  9,16515 
 rAB  rAC 

 


rBA  i  6 j  k  rBA  6,16441





rBC  3 i  2 j  5 k  rBC  6,16441
 
rBA .rBC  4
 
 rBA .rBC 
o
  arc cos 
   96,04
 rBA  rBC 




rCB  3 i  2 j  5 k




rCA  2 i  8 j  4 k
 
rCB .rCA  42
 
 rCB .rCA

  arc cos 

 rCB  rCA
Sábado, 14 de agosto de 2010

 rCB  6,16441

 rCA  9,16515

  41,98 o


4
[email protected] – www.profwillian.com
UCDB – Eng. Sanitária e Ambiental
Mecânica Aplicada – Prova P1 Modelo
5- Duas barras são usadas para suportar uma carga P=5 kN. O comprimento de AB é 75 cm, o de
AC é 100 cm. Encontre os esforços normais nas barras AB e AC para o perfeito equilíbrio estático
do nó A, ou seja, calcule os esforços nas barras AB e AC para que a resultante do sistema de forças
ao redor de A seja igual a zero.
40º
Solução:
BD
Para encontrar o lado AD, temos que:
AD
sen (40 o ) 

100
AD  100  sen (40 o )  64,2788 cm
o ângulo :
AD
64,2788
cos() 
 cos() 
75
75
o
  31,013  0,541279 rad
CD
40º
AD
FAB

FAC
40º
Equações de equilíbrio onde FAB e FAC são as forças nas hastes AB e AC, respectivamente.
(1)
 Fx  0   FAB  sen()  FAC  cos(40 o )  0
F
y
 0  FAB  cos()  FAC  sen(40 o )  P  0
(2)
Assim temos:
FAC  FAB 
sen ()
cos(40 o )
FAB  cos()  FAB 
FAB 
(1)
sen ()
 sen (40 o )  5
cos(40 o )
5
 3,87783 kN
cos()  sen ()
(2)
 FAC  3,87783 
sen ()
 2,60818 kN
cos(40 o )
Resposta: As forças nas barras AB e AC são: 3,878 kN e 2,608 kN, respectivamente.
Sábado, 14 de agosto de 2010
5
[email protected] – www.profwillian.com
UCDB – Eng. Sanitária e Ambiental
Mecânica Aplicada – Prova P1 Modelo
6- Determine a força em cada barra necessária para suportar a força F = 5 kN. O ponto A está a 4 m
acima do plano xy. Considere cada quadriculado 1 m × 1 m.
F=5 kN
z
A
O
y
C
B
x
D
Solução:
F=5 kN
z
A
FAD
O
As coordenadas dos pontos são:
FAC
FAB
y
C
A(2,
B(3,
C(0,
D(4,
4,
8,
3,
1,
4)
0)
0)
0)
B
x
D








rAB
(3  2) i  (8  4) j  (0  4)k
FAB  FAB  
 0,174078 i  0,696311 j  0,696311 k FAB
rAB
12  4 2  4 2








rAC
(0  2) i  (3  4) j  (0  4)k
FAC  FAC  
  0,436436 i  0,218218 j  0,872872 k FAC
rAC
2 2  12  4 2








rAD
(4  2) i  (1  4) j  (0  4)k
FAD  FAD  
 0,371391 i  0,557086 j  0,742781 k FAD
rAD
2 2  32  4 2






O equilíbrio é conseguido quando:
 Fx  0  FAB 0,174078  FAC 0,436436  FAD 0,371391  0
F
F
y
 0  FAB 0,696311  FAC 0,218218  FAD 0,557086  0
z
 0  FAB 0,696311  FAC 0,872872  FAD 0,742781  5  0
FAB  2,20945 kN

FAC  2,42348 kN
FAD  1,81232 kN
Resposta: As forças FAB, FAC e FAD têm módulos 2,20945 kN, 2,42348 kN e 1,81232 kN,
respectivamente.
Sábado, 14 de agosto de 2010
6
[email protected] – www.profwillian.com