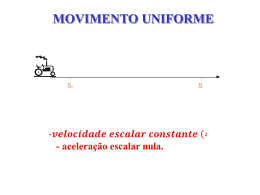
TUTORIAL – 1R Data: Aluno (a): Série: 3ª Ensino Médio Turma: Equipe de Física Física Movimento Uniforme Quando um móvel se desloca com uma velocidade constante, diz-se que este móvel está em um movimento uniforme (MU). Particularmente, no caso em que ele se desloca com uma velocidade constante em trajetória reta, temse um movimento retilíneo uniforme. Uma observação importante é que, ao se deslocar com uma velocidade constante, a velocidade instantânea deste corpo será igual à velocidade média, pois não haverá variação na velocidade em nenhum momento do percurso. A equação horária do espaço pode ser demonstrada a partir da fórmula de velocidade média. Atenção: Por convenção, definimos que, quando um corpo se desloca em um sentido que coincide com a orientação da trajetória, ou seja, para frente, então ele terá uma v>0 e um >0 e este movimento será chamado movimento progressivo. Analogamente, quando o sentido do movimento for contrário ao sentido de orientação da trajetória, ou seja, para trás, então ele terá uma v<0 e um movimento será dado o nome de movimento retrógrado. <0, e ao Diagrama s x t Existem diversas maneiras de se representar o deslocamento em função do tempo. Uma delas é por meio de gráficos, chamados diagramas deslocamento versus tempo (s x t). No exemplo a seguir, temos um diagrama que mostra um movimento retrógrado: Sabemos então que a posição inicial será a posição = 50m quando o tempo for igual a zero. Também sabemos que a posição final s=10m se dará quando t=2s. A partir daí, fica fácil utilizar a equação horária do espaço e encontrar a velocidade do corpo: Colégio A. LIESSIN – Scholem Aleichem -1- NANDA/MARÇO/2014 - 197 Diagrama v x t Em um movimento uniforme, a velocidade se mantém igual no decorrer do tempo. Portanto seu gráfico é expresso por uma reta: Dado este diagrama, uma forma de determinar o deslocamento do móvel é calcular a área sob a reta compreendida no intervalo de tempo considerado. Movimento Uniformemente Variado Também conhecido como movimento acelerado, consiste em um movimento onde há variação de velocidade, ou seja, o móvel sofre aceleração à medida que o tempo passa. Mas se essa variação de velocidade for sempre igual em intervalos de tempo iguais, então dizemos que este é um Movimento Uniformemente Variado (também chamado de Movimento Uniformemente Acelerado), ou seja, que tem aceleração constante e diferente de zero. O conceito físico de aceleração, difere um pouco do conceito que se tem no cotidiano. Na física, acelerar significa basicamente mudar de velocidade, tanto tornando-a maior, como também menor. Já no cotidiano, quando pensamos em acelerar algo, estamos nos referindo a um aumento na velocidade. O conceito formal de aceleração é: a taxa de variação de velocidade numa unidade de tempo, então como unidade teremos: Aceleração Assim como para a velocidade, podemos definir uma aceleração média se considerarmos a variação de velocidade em um intervalo de tempo Colégio A. LIESSIN – Scholem Aleichem , e esta média será dada pela razão: -2- NANDA/MARÇO/2014 - 197 Velocidade em função do tempo No entanto, quando este intervalo de tempo for infinitamente pequeno, ou seja, aceleração instantânea do móvel. Isolando-se o , tem-se a : Mas sabemos que: Então: Entretanto, se considerarmos , teremos a função horária da velocidade do Movimento Uniformemente Variado, que descreve a velocidade em função do tempo [v=f(t)]: Posição em função do tempo A melhor forma de demonstrar esta função é através do diagrama velocidade versus tempo (v x t) no movimento uniformemente variado. O deslocamento será dado pela área sob a reta da velocidade, ou seja, a área do trapézio. Onde sabemos que: logo: ou Interpretando esta função, podemos dizer que seu gráfico será uma parábola, pois é resultado de uma função do segundo grau. Colégio A. LIESSIN – Scholem Aleichem -3- NANDA/MARÇO/2014 - 197 Equação de Torricelli Até agora, conhecemos duas equações do movimento uniformemente variado, que nos permitem associar velocidade ou deslocamento com o tempo gasto. Torna-se prático encontrar uma função na qual seja possível conhecer a velocidade de um móvel sem que o tempo seja conhecido. Para isso, usaremos as duas funções horárias que já conhecemos: (1) (2) Isolando-se t em (1): Substituindo t em (2) teremos: Reduzindo-se a um denominador comum: Exercícios 1. A escada rolante de uma galeria comercial liga os pontos A e B em pavimentos consecutivos a uma velocidade ascendente constante de 0,5 m/s, conforme mostrado na figura. Se uma pessoa consegue descer contra o sentido de movimento da escada e leva 10 segundos para ir de B até A, pode-se afirmar que sua velocidade, em relação à escada, foi em m/s igual a: Colégio A. LIESSIN – Scholem Aleichem -4- NANDA/MARÇO/2014 - 197 a) 0,0 b) 0,5 c) 1,0 d) 1,5 e) 2,0 2. Um homem, caminhando na praia, deseja calcular sua velocidade. Para isso, ele conta o número de passadas que dá em um minuto, contando uma unidade a cada vez que o pé direito toca o solo, e conclui que são 50 passadas por minuto. A seguir, ele mede a distância entre duas posições sucessivas do seu pé direito e encontra o equivalente a seis pés. Sabendo que três pés correspondem a um metro, sua velocidade, suposta constante, é: a) 3 km/h b) 4,5 km/h c) 6 km/h d) 9 km/h e) 10 km/h 3. Quando navega a favor da correnteza, um barco desenvolve 40 km/h; navegando contra, faz 30 km/h. Para ir de A até B, pontos situados na mesma margem, gasta três horas menos que na volta. A distância entre A e B é de: a) 360 km b) 420 km c) 240 km d) 300 km e) 180 km 4. Você vai para a faculdade com a velocidade média de 30 km/h e volta com a velocidade média de 20 km/h. Para ir e voltar gastando o mesmo tempo, sua velocidade média deveria ser a) 25 km/h b) 50 km/h c) 24 km/h d) 10 km/h e) 48 km/h 5. Dois veículos, A e B, se movem ao longo de uma estrada horizontal e reta esuas posições variam com o tempo conforme o gráfico mostrado abaixo. Colégio A. LIESSIN – Scholem Aleichem -5- NANDA/MARÇO/2014 - 197 Sobre o movimento de A e B podemos afirmar: a) no instante de tempo t = to as velocidades dos dois veículos são iguais; b) A e B percorrem uma mesma distância entre os instantes t = 0 e t =to ; c) no instante de tempo t = to A e B encontram-se igualmente afastados da posição x = 0; d) no instante de tempo t = to a aceleração de A é maior do que a aceleração de B; e) em qualquer instante de tempo a velocidade de B é maior do que a velocidade de A. 6. Duas partículas, A e B, que executam movimentos retilíneos uniformemente variados, se encontram em t = 0 na mesma posição. Suas velocidades, a partir desse instante, são representadas pelo gráfico abaixo. As acelerações experimentadas por A e B têm o mesmo módulo de . Com base nesses dados, é correto afirmar que essas partículas se encontrarão novamente no instante a) 10 s b) 50 s c) 100 s d) 500 s e) 250 s 7. Um avião a jato, para transporte de passageiros, precisa atingir a velocidade de 252 km/h para decolar em uma pista plana e reta. Para uma decolagem segura, o avião, partindo do repouso, deve percorrer uma distância máxima de 1 960 m até atingir aquela velocidade. Para tanto, os propulsores devem imprimir ao avião uma aceleração mínima e constante de: a) 1,25 m/s². b) 1,40 m/s². c) 1,50 m/s². d) 1,75 m/s². e) 2,00 m/s². 8. Dois automóveis A e B se movimentam sobre uma mesma trajetória retilínea, com suas velocidades variando com o tempo de acordo com o gráfico a seguir. Sabe-se que esses móveis se encontram no instante 10 s. Colégio A. LIESSIN – Scholem Aleichem -6- NANDA/MARÇO/2014 - 197 A distância entre eles, no instante inicial (t = 0 s), era de a) 575 m b) 425 m c) 375 m d) 275 m e) 200 m 9. Um motorista conduz seu automóvel pela BR-277 a uma velocidade de 108 km/h quando avista uma barreira na estrada, sendo obrigado a frear (desaceleração de 5 m/s²) e parar o veículo após certo tempo. Pode-se afirmar que o tempo e a distância de frenagem serão, respectivamente: a) 6 s e 90 m. b) 10 s e 120 m. c) 6 s e 80 m. d) 10 s e 200 m. e) 6 s e 120 m. 10. Em uma prova internacional de ciclismo, dois dos ciclistas, um francês e, separado por uma distância de 15 m à sua frente, um inglês, se movimentam com velocidades iguais e constantes de módulo 22 m/s. Considere agora que o representante brasileiro na prova, ao ultrapassar o ciclista francês, possui uma velocidade constante de módulo 24 m/s e inicia uma aceleração constante de módulo 0,4 m/s², com o objetivo de ultrapassar o ciclista inglês e ganhar a prova. No instante em que ele ultrapassa o ciclista francês, faltam ainda 200 m para a linha de chegada. Com base nesses dados e admitindo que o ciclista inglês, ao ser ultrapassado pelo brasileiro, mantenha constantes as características do seu movimento, assinale a alternativa correta para o tempo gasto pelo ciclista brasileiro para ultrapassar o ciclista inglês e ganhar a corrida. a) 1 s. b) 2 s. c) 3 s. d) 4 s. e) 5 s. Gabarito 1. d 2. c 3. a 4. c 5. c 6. d 7. a 8. a 9. a 10. e Colégio A. LIESSIN – Scholem Aleichem -7- NANDA/MARÇO/2014 - 197
Baixar