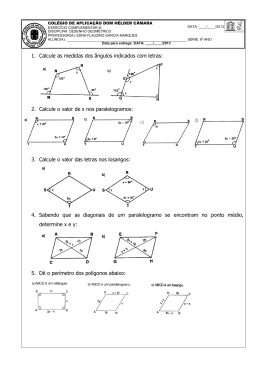
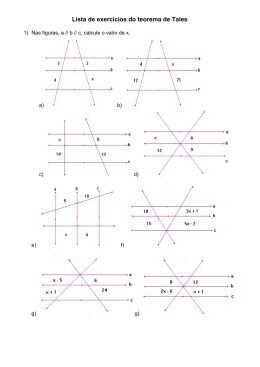
Lista de Exercícios de Férias
Matemática – 8° Ano
ÂNGULOS:
1) Sendo a // b, calcule x, y e z indicados em cada figura:
a)
b)
x
a
65°
z
y
s
3x + 30°
y
z
x + 10°
b
a
2) Calcule x, y e z, sabendo que r e s são paralelas:
a)
r
b)
80°
z
s
x
150°
y
b
r
s
y
z
3x
2x
120°
3) Sendo r paralela a s, qual é o valor de x?
a)
b)
x
60°
r
r
x
70°
130°
s
□
20°
s
4) Duas retas paralelas e uma transversal determinam dois ângulos correspondentes cujas
medidas são 2x – 30° e x + 10°. Calcule as medidas dos ângulos obtusos determinados
por essas retas.
5) Qual é a soma?
a) 120° 28’7” + 42° 12’ 32”
b) 50° 40’ + 25° 24’
c) 48° 52” + 52’ 48”
d) 57° 32” + 4’ 40”
6) Qual é a diferença?
a) 90° 50’ 55” – 42° 37’ 15”
c) 5° - 3° 12’
b) 40° 15’ – 25° 50’
d) 35° 12”- 10° 54’
7) Qual é o produto?
a) (40° 25’ 33”) x 2
b) (5° 52”) x 4
c) (50’ 30”) x 10
d) ( 15° 35’ 58”) x 5
8) Qual é o quociente?
a) (81° 54’ 39”) : 3
b) (5° 14’) : 3
c) (47° 12’) : 2
d) (139° 42’ 20”) : 5
9) A quinta parte do complemento de um ângulo rÔs é 12°. Quanto mede rÔs?
10) Dois ângulos são suplementares e a diferença entre eles é 32°. Quanto mede o ângulo?
TRIÂNGULOS:
1) Em um triângulo isósceles o lado diferente mede 12 cm. Calcule as medidas dos outros
dois lados, sabendo que o seu perímetro é de 40 cm.
2) O triângulo ABC é eqüilátero. Sabendo que AB = 15 – y, BC = 2x – 7 e AC = 9, determine x
e y.
A
15 – y
B
9
2x – 7
C
3) Calcule o valor do x e classifique o triângulo em relação aos ângulos:
a)
A
b)
D
c)
60°
30°
20°
C
E
F
B
4) Determine os valores de x e y em cada item:
a)
A
b)
2x + 10°
A
80°
Y
B
2x–10°
□
x
x
x
55° 30°
x
150°
C
y
B
x
40°
D
C
5) O triângulo ABC é isóscele de base BC. Sabendo que AB = 2x – 7 e AC = x + 5, determine
x.
6) O triângulo ABC é isóscele de base BC. Sabendo que AB = 3x – 10, BC = 2x + 4 e AC = x +
4, calcule a medida de BC:
A
3x – 10
B
x+4
2x + 4
C
7) Determine os lados de um triângulo da figura sabendo que ele tem 60 cm de perímetro.
x+3
x–7
x-2
8) Calcule x e y em cada uma das figuras abaixo:
a)
b)
x
120°
60°
x 40° y
30°
y
80°
50° 110°
30°
9) Determine a medida dos ângulos internos do triângulo, sabendo que os ângulos externos
medem em graus, respectivamente: x, x + 10° e x – 10°.
EQUAÇÕES:
1) Resolva as equações, sendo x Є Q:
a) 9 + 5y = -91
b) 0,2m + 1 = -4
c) 5(3y – 2) -1 = -6
d) 4n – (1 – n) = 4
2) Encontre o conjunto solução de cada equação:
a) 10 = 3(z – 2) – (z – 18)
c) t – 3(4 – t) = - 96
b) 2(7x – 1) -3(4 – 14x) = -6
d) -15 = 3(x – 1) + 2x
3) O comprimento de um retângulo é o dobro da largura menos 1 cm. O perímetro do retângulo é 52
cm. Qual é a largura do retângulo?
4) Carmem tem o triplo da idade de sua filha. Daqui a cinco anos a soma das suas idades será 70 anos.
Qual a idade atual de Carmem?
5) Júlia disse: “Pensei num número. Multipliquei-o por 27. Adicionei 361 ao produto. Subtraí 720 da
soma. Obtive 1 342. Em que número pensei?”
6) Resolva as equações:
a)
c)
b)
d)
7) Dividir um número por 4 dá o mesmo resultado que subtrair 14 do dobro desse número. Qual é
esse número?
8) Juntos dois terrenos retangulares ocupam uma área de 213 m2. Qual é o perímetro de cada um?
5m
m
m
6m
9) Descubra qual é o número que, se somarmos a metade, a quarta parte e a sexta parte desse
número com ele mesmo, obtemos 138.
10) Encontre um número inteiro que é raiz desta equação:
INEQUAÇÕES:
1) Resolva as inequações:
a) 2x – 4> 10
b) 2(n – 5) ≥ n
c) 1 – 2(x – 1) < 2 - x
d) 4 – (2 – 4y) > 8y
2) Determine o conjunto solução de cada inequação:
a)
b)
3) Qual é o menor valor inteiro que podemos atribuir à incógnita x na figura abaixo para que o
perímetro dessa figura seja maior que 40 unidades de comprimento?
3x
x
2x
1
x
4
4) Indicando por x o número de letras de uma palavra, assinale a palavra para a qual a inequação
x < 6 pode ser aplicada:
a) matemática
c) quadrados
e) geometria
b) professor
d) lados
5) Numa sala de aula há x alunos. Se um dia faltarem 15 alunos, o número de alunos presentes
será menor que os
do número total de alunos que há na sala. Escreva a inequação que
representa essa situação e diga qual é o maior número inteiro de alunos que pode ter essa sala
de aula.
SIMETRIA:
1) Represente na malha quadriculada a figura simétrica, dado o seu eixo de simetria:
I
I
I
Atenção
Todos os exercícios devem conter os cálculos e podem ser respondidos em folhas separadas na
sequência, ou podem ser respondidos na própria folha desde que seja feira uma formatação para ter
espaça suficiente.
Boas férias e se divirtam muito!
Prof: Elvis Miranda