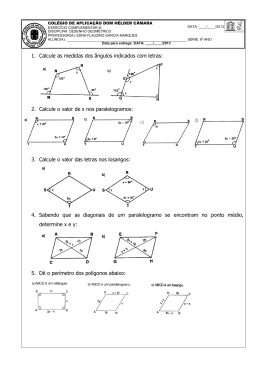
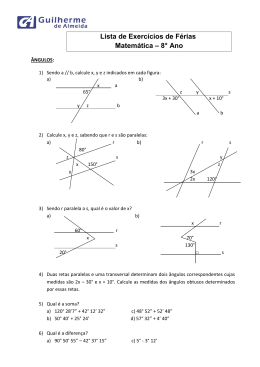
CIANSP - COLÉGIO NOSSA SENHOR A DA PIEDADE
R u a M o n s e n h o r D o m i n go s P i n h ei r o , 3 5 – C a l a f a t e / B H
F o n e : ( 3 1 ) 3 3 3 4 6 9 1 3 - s ec r et a r i a @ c o l e gi o p i ed a d e. c o m . br
76 Anos Educando para a Vida
DISCIPLINA: MATEMÁTICA
PROFESSOR(A):HELEN CAROLINA
ANO:2015
ENS: FUND.II
DATA ENTREGA: 17/12/15
TRABALHO DE RECUPERAÇÃO 8º ANO
VALOR: 20
NOTA:
ALUNO(A):
Nº:
Caro(a) aluno (a) DO 8º ANO: O trabalho precisa estar completo, ou seja, conter as perguntas (podendo
elas ser xerocadas e coladas ou manuscritas) e as respostas (com raciocínio). Poderá ser feito em Folha almaço
ou A4. Fazer capa com o cabeçalho completo. Deverá ser entregue impreterivelmente no dia da prova.
É chegada a hora de refletir sobre o seu trabalho durante o ano, aproveitar o que foi positivo, reavaliando os
aspectos que precisam ser melhorados e mãos à obra. Faça o seu plano de estudo diário, reservando um período
para resolução de tarefas de casa, pesquisas e revisão de conteúdo. O trabalho está baseado nas atividades
trabalhadas em sala, portanto use o caderno como fonte de estudo. Faça o trabalho com capricho e atenção. As
unidades do livro de matemática podem ser usados como fonte de estudo. Conte comigo para o esclarecimento
de suas dúvidas e para estar ao seu lado nessa caminhada.
Helen Carolina
1- Coloque no diagrama ao lado as letras dos
conjuntos numéricos 𝒩, 𝒵, 𝒬, 𝐼 𝑒 ℛ de forma
adequada. Depois distribua os seguintes
números nos locais corretos:
2- Na sua caminhada matinal, Mariana deu 10
voltas em uma praça com raio de 30m. Nessa
caminhada, ela percorreu +ou - do que 2km?
4- Indique a sentença falsa e justifique.
a) Todo número natural é inteiro.
b) Todo número inteiro é real.
c) Todo número racional é inteiro.
d) Todo número irracional é real.
49
3
3
3
6- Verifique se 𝑥 = 7 . √64 + (1 − 5) : 5 + (1 + 5)
é inteiro.
1,70m de altura e 70kg?
a) Sobrepeso com IMC 29
b) Abaixo do peso com IMC 16,7
c) Normal com IMC 24,2
d) Obesidade com IMC acima de 30
8- Escreva os números reais abaixo em ordem
crescente.
5- Guilhermina preparou um bolo de aniversário e
o colocou exatamente sobre uma bandeja circular
de 30cm de diâmetro. Depois, decorou com uma
fita de papel em volta do bolo. Qual é a medida
do comprimento dessa fita de papel?
4
7- O IMC é a sigla para índice de massa corporal,
que permite a uma pessoa fazer o controle de
seu "peso". Usamos a fórmula ao lado para
calcularmos o IMC de uma pessoa.
Em que faixa da tabela está uma pessoa com
9- (UFMA-adaptada) Quantos números inteiros
pertencem ao intervalo [−√12, √19]?
a) 6
b) 7 c) 8 d) 10
2
10-(UFRN) O valor de 0,333… é:
11- Qual é o polinômio que multiplicado
por 3x² - 7 dá 15x³ - 6x² - 35x + 14?
12- Em certa cidade, um motorista de táxi cobra
R$4,50 de bandeirada mais R$0,90 por
quilômetro rodado. Escreva a fórmula que indica
a quantia a pagar(Q) se o número de quilômetros
rodados for "n".
13- Observe a
figura plana
abaixo:
Escreva a
expressão
algébrica que
representa em
metros
quadrados:
a) a área da região colorida
b) a área da região branca.
c) a área total
d) o perímetro de toda figura.
a) (x+3)² + x² - 7x
b) (x+2)² - (x+4)² + 4x + 12
19- Em um clube foram
construídas duas
piscinas que estão
representadas pelas
regiões poligonais
ao lado.
a) Escreva o
perímetro do
retângulo na
forma reduzida usando polinômio.
b) Escreva o perímetro do trapézio na forma
reduzida usando polinômio.
c) Se o perímetro da piscina retangular é de
24m, qual é o valor de x?
d) Se a piscina em formato de trapézio tem
perímetro de 84m e a=7m, qual é o valor de b?
20- Relacione as COLUNAS:
14- Complete o quadro das fórmulas dos
produtos notáveis:
Quadrado da
Soma
Quadrado da
Diferença
Produto da
Soma pela
diferença
Cubo da Soma
( a +b)² =
= a²-2ab+b²
(a+b). (ab)=
(a+b)³=
(a -b)³= a³3a²b+3ab²+b³
15- Se A= x²+1 e
B= -2x² + x + 2,
determine o valor de -2A+3B
16- A figura ao
lado mostra a
planta de um
estacionamento.
Determine a
expressão "E" que
indica a área do
estacionamento e
depois calcule
essa quantidade
para x=10.
17- Efetue:
21- A área da região retangular a seguir pode
ser indicada por 3x² - 4x + 1.
a) Descubra a expressão que representa a
largura.
b) Descubra o valor de x para o qual o perímetro
é de 52 unidades.
22) Fatore os polinômios:
a) 3x²y+6xy²-9z
b) ab+3b-7a-21
c) n² - 10n+100
d) 64x² -9
b) (6𝑥 4 − 10𝑥³ + 9𝑥² + 9𝑥 − 5): (2𝑥 2 − 4𝑥 + 5)
22) Fatore:
a) a³ + 1000
b) (2a - 1)³
18- Desenvolva reduzindo os termos
semelhantes.
23-Resolva a equação fracionária
2
−1
a) 𝑥²−4 = 𝑥+2
a)
(21𝑥 3 −𝑥 2 )−(6𝑥 3 +9𝑥 2 )
3𝑥 2 +2𝑥 2
1
2
3
amigos. Cada um recebeu 7 minhocas.
Quantos filhos Paulo tem?
b) 𝑥−3 = 𝑥²−9 + 𝑥+3
24) Resolva as equações literais abaixo na
incógnita x:
A) 2x+2a=20
B)
x 1 x


a ab b
com
a0 b0
31- Analise os sistemas quanto a classificação e
quanto ao gráfico que representa e relacione as
colunas
IIIIx  y  3
II
x

y


3
x  2 y  1

x  y  0

3x  2 y  16
25- O peso de Camila e de seu gato Tico, juntos
é de 32kg. O peso de Camila é 7 vezes o de
Tico. Qual o peso de cada um?
26- Numa sala retangular, o comprimento é 3m
maior do que a largura. Sabendo que seu
perímetro é de 26m, quanto medem a largura e
o comprimento dessa sala?

2 x  4 y  2
(A) Sistema
Impossível (SI)
(B) Sistema
Possível
Indeterminado
(SPI)
(C) Sistema
Possível
Determinado
(SPD)
1-
2-
3-
27- Josias comprou 5 canetas e 3 lápis e gastou
R$21,10. Mariana comprou 3 canetas e 2 lápis e
gastou R$12,90. Fernando comprou 4 canetas e
5 lápis. Quanto ele gastou?
28 – Observe a figura abaixo. O gráfico formado
pelo trajeto das aranhas até a formiga pode ser
representado por qual sistema?
32- Duas empresas de telefonia, "Fale igual
pobre na chuva" e "Fale igual Maria"
apresentam os seguintes planos mensais:
Fale igual
pobre na Chuva
Fale igual
Maria
R$30,00 (por 100 min.de utilização)
+ R$0,20 por minuto excedente.
R$20,00 (por 100 min.de utilização)
+ R$0,25 por minuto excedente.
Quantos minutos deve utilizar um cliente para
que seja mais vantajoso para ele optar pela
operadora "Fale igual pobre na chuva"?
33- Considerando r//s, determine, em graus, o
valor de x:
a)
2 x  3 y  5
x  y  2
x  y  7
c) 
x  y  3
a) 
x  y  3
x  y  0
2 x  y  7
d) 
x  2 y  3
b) 
b)
29 – Simplifique as frações algébricas:
a)
c)
𝒙²−𝟓𝒙+𝒙𝒚−𝟓𝒚
𝟕𝒙+𝟕𝒚
𝒙
𝟓
−
𝒙²−𝟒
𝒙+𝟐
𝟐𝒚²−𝟏𝟎𝒚
𝒚−𝟓
b)
d)
𝒂²
𝒙𝒚²
𝒂
𝒙²𝒚
30- Paulo convidou seus filhos e seus amigos
para uma pescaria. Ele tinha 49 iscas de
minhoca e as dividiu entre os filhos e os 4
34 - Se um triângulo tem dois lados medindo
6cm e 3cm, qual é o maior número inteiro que
pode indicar a medida do terceiro lado em
centímetros? E o menor?
35- (Ufscar-SP) Na figura abaixo, calcule o
valor, em graus, da diferença x - y
36- Determine a medida, em graus, de cada
ângulo assinalado:
a)
39- Um trapézio é isósceles e a medida de um
dos seus ângulos agudos corresponde a 2/3 da
medida de um dos seus ângulos obtusos. Quais
são as medidas dos quatro ângulos internos
desse trapézio?
40 - Uma corda foi
esticada do topo deste
prédio até o chão. O
ângulo determinado no
chão pode ser medido:
62º. Qual é a medida
do ângulo no topo
desse prédio?
41- Dado um
triângulo
isósceles PQR,
PQ  PR . Qual
é o valor de x,
em graus?
42 - Considere cada um dos quadriláteros
abaixo e determine o valor de cada uma das
medidas dos ângulos internos:
b)
43- Calcule o valor de x e y com base nas
figuras e nas informações dadas.
a) AN é uma bissetriz do ABC
37- Marque a alternativa FALSA:
a) Todo retângulo é paralelogramo.
b) Todo quadrado é retângulo.
c) Todo paralelogramo é losango.
d) Todo quadrado é losango.
38- No centro da
estrela há um
pentágono regular.
Calcule os ângulos
das pontas da estrela.
b) FP é uma altura do EFG
10) Reta que
corta uma
44- Um carro, com certa velocidade média,
percorre os 400km que separam Taubaté (SP)
de Ribeirão Preto (SP) em x horas. Outro carro,
com a mesma velocidade média do primeiro,
percorre os 800km de Araraquara (SP) a
Brasília (DF) em (x+4) horas. Determine o
número de x de horas.
circunferência em dois pontos distintos.
45 - Observe o triângulo ABC desenhado ao
lado. Considere as informações abaixo e calcule
m(BîE).
* "I" é o incentro do
ABC
* m(Â)=82º
* m( B̂ )=62º
48 - Calcule x, em seguida dê o valor dos
ângulos :
46- Determine o valor das letras que aparecem
no trapézio abaixo:
47- Complete a cruzadinha ao lado:
1) Polígono de 4 lados
2) Ponto de encontro das alturas de um
triângulo
3) Paralelogramo que tem quatro lados
congruentes e quatro ângulos retos.
4) Dois segmentos da mesma medida.
5) Ponto de encontro das medianas de um
triângulo.
6) Corda que passa pelo centro de uma
circunferência.
7) Triângulo que possui apenas dois lados
congruentes.
8) Segmento que une dois vértices não
consecutivos do polígono.
9) Ponto de encontro das bissetrizes de um
triângulo.
49- Os 400 alunos do 6º ao 9º ano do período
da tarde da escola de João estão distribuídos de
acordo com o gráfico de setores:
Com base no
gráfico, determine a
porcentagem e o
número de alunos
correspondentes a
cada ano nesta
tabela:
Ano Porcentagem Número de alunos
6º
7º
8º
9º
50- Sendo PT e PQ segmentos congruentes e
tangentes à circunferência, determine suas
medidas sabendo que o raio da circunferência
mede 3,5cm e que o perímetro do quadrilátero
PTOQ é de 28cm.
55 - Determine o
comprimento da
curva que separa a
parte pintada da
parte em branco.
56- Em um triângulo
ABC , o lado AB mede
4cm a menos do que a medida do lado AC , a
medida do lado BC é igual a
51- Descubra o valor das incógnitas em graus:
a)
b)
c)
3
da medida do
5
lado AC , e o perímetro é de 22cm. Determine a
medida dos três lados desse triângulo.
57- Calcule a
área da região
colorida
abaixo. Os
valores são
dados em
centímetros.
52 - Na
circunferência da
figura abaixo, "O" é
o centro, MÂH
mede 2x-1º e MÔH
mede 3x+18º
O valor de x é:
53- José vai
cercar com
uma tela um
terreno que
tem as
medidas
indicadas na
figura. Cada
metro de tela
custa R$ 6,50. Quanto ele vai gastar?
54- De acordo
com a figura ,
o valor de â +
ê vale:
58 - A figura ao lado é uma região plana ABCD
cujo contorno é um losango, com as seguintes
medidas:
AB=13cm,
AC= 24cm e
BD=10cm.
Determine:
a) as medidas dos lados BC, CD e DA
b) a medida da diagonal maior e menor do
losango
c) a área da região ABCD
d) a área da região EFGH
59 - Um fio vai ser esticado do topo deste
prédio até um ponto
no chão, como
indica a figura. Qual
deve ser o
comprimento do fio?
(Use a relação de
Pitágoras para
resolver).
60- Um tanque
com a forma de
bloco retangular
tem as dimensões
citadas ao lado. Se
uma torneira
despeja 25 litros
de água por
minuto, em quanto
tempo ela encherá esse tanque?
61 - Qual é o
volume do aquário?
(Dê a resposta em
cm³ e litro, sabendo
que 1dm³ = 1 litro)
b) A face 5 voltada para cima no lançamento do 2º
dado
c) Um número maior que 4 no lançamento do 1º
dado
d) A face 3 voltada para cima o lançamento do 1º
dado
66. Marisa jogou
um dado sete
vezes. Verifique as
pontuações obtidas
e calcule:
a) a média aritmética dos pontos obtidos
b) a moda dos pontos obtidos
c) a média aritmética dos pontos obtidos
d) a moda dos pontos obtidos
67. Calcule o valor de x para que a moda de 2x -1,
7 e 9 seja igual a 9.
62- Descubra a área de toda a região
63. Valéria e Alexandre inventaram uma
brincadeira em que retirariam ao acaso uma
ficha colorida de uma sacola e de acordo com a
cor da ficha, cada um receberia uma pontuação.
Quem fizesse mais pontos ganharia um prêmio.
Eles colocaram na sacola 4 fichas amarelas, 3
brancas e 2 pretas. Retirando-se aleatoriamente
uma ficha da sacola, a probabilidade de ela ser:
a) amarela b) branca c) preta
64. No fim do ano letivo, os alunos do 8º ano A
resolveram fazer uma brincadeira conhecida por
amigo secreto. O sorteio é feito da seguinte
maneira: escreve-se o nome de cada participante
em um pequeno pedaço de papel; misturam-se
todos os papéis e, então, cada um retira
aleatoriamente um nome. Se essa turma tem 30
alunos, entre os quais 20 são meninas e 10 são
meninos. Sobre o sorteio, qual a probabilidade de
um aluno tirar :
a) um menino a) uma menina c) seu nome
65. Considerando os dados ao lado, calcule a
probabilidade do evento abaixo ocorrer:
a) A soma das faces voltadas para cima igual a 2
no lançamento dos dois dados
68. Estas são as alturas em centímetros de um
grupo de crianças.
Sobre essas
informações calcule:
a) a média de altura
desse grupo
b) a mediana de
altura desse grupo
c) a mediana de
altura desse grupo
d) a moda de altura
desse grupo
69. Calcule o valor de x para que a média
aritmética de x+1, 2x e x-4 seja igual a 7.
70. Veja os gastos de uma pessoa com
alimentação em uma determinada semana. A
média diária de gastos é:
71. Um cubo de aresta 10cm está com água até
certa altura. Em seu interior é colocada um pedra
que faz a altura da água subir 4cm sem que a
água derrame. Qual é o volume da pedra colocada
em seu interior?
72. Pedro ganhou uma
pirâmide de acrílico com
as seguintes
característica: a base é
uma região retangular de
5cm por 6cm e a altura
é de 9cm. Qual é o
volume dessa pirâmide?
73. Para ir
de A até B
pode-se
fazer
vários
caminhos.
Sobre
a
distância
em metros:
a) A linha de A até B
b) A curva
c) A curva de A até C e passando pela linha de C
até B