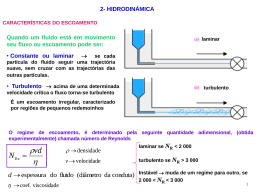
FÍSICA
SEGUNDO ANO
Prof. Giovani
[email protected]
HIDROSTÁTICA
Pressão: é a relação entre a força e a área de
contato onde a força é exercida.
F
p=
A
Pressão hidrostática: é pressão causada por fluidos
p = μ.g.h
Na figura ao lado o
líquido causa pressão
sobre o fundo do
recipiente. Quanto mais
cheio o copo maior a
pressão.
Unidades de pressão: Pa(N/m²), lb/pol², Kgf/cm², atm etc.
Pressão atmosférica
É a pressão exercida pelos gases atmosféricos
Pressão atmosférica ao nível do mar
1atm = 105N/m2 = 105Pa = 760mmHg = 76cmHg = 10mca
Pressão atmosférica acima do nível do mar
Ceturis paribus: temperatura, velocidade do ar e umidade,
a pressão em altitudes é menor que 1atm
Pressão
em
fluidos
Pressão efetiva
ou hidrostática
p   . g .h
Pressão
total ou
absoluta
p  p atm   . g .h
HIDROSTÁTICA
Densidade absoluta ou massa específica: é a
relação entre a massa e o volume do corpo.
m
Unidades: Kg/m³ e g/cm³
μ=
V
1000 Kg/m³ = 1g/cm³
Densidade relativa: é a relação entre as densidades
de dois corpos ou substâncias A e B.
μA
dAB =
μB
É adimensional (não tem unidades)
Peso específico: é a relação entre o peso e o volume
de dois corpos ou substâncias.
P
ρ=
V
ρ= g. μ
Unidades: N/m³ e dyn/cm³
Exemplo
(UFSM) Observe a seguinte figura:
B
ℓ = 30 m
30°
A
O tubo da figura tem sua extremidade “A” fechada e sua
extremidade “B” aberta. Esse tubo está totalmente
preenchido com água. A pressão absoluta exercida na base
“A”, é da ordem de:
Solução:
a) 1,5 atm
A pressão atmosférica é 1atm ou
b) 2,0 atm
100.000Pa
pA = patm + μ.g.h
X c) 2,5 atm
d) 3,0 atm
Mas observe: h = 30.sen30º = 15m
e) 4,0 atm
pA = 100.000 + 1000.10.15
pA = 250.000Pa
pA = 2,5atm
Princípio de Pascal
“A variação de pressão provocada em um
ponto de um fluído em equilíbrio se transmite
integralmente a todos os pontos do fluído e das
paredes do recipiente que o contém.”
Aplicação: Prensa hidráulica
Ex.: Sistema de freio
Macaco hidráulico
Hidráulico de trator
Elevador hidráulico
A força é ampliada mas a energia é
conservada. Logo, o êmbolo de
maior área tem maior força e
menor deslocamento.
F1
A1
=
F2
A2
Exemplo
(PEIES 99) Observe o esquema de uma
prensa hidráulica usada nos postos de
serviço automotivo, a qual tem
funcionamento baseado no princípio de
__________, que garante que qualquer
pressão exercida no pistão  aparece
_________ no pistão .
Assinale a alternativa que completa,
corretamente, as lacunas.
a) Pascal – menor
Solução:
b) Arquimedes – igual
As prensas hidráulicas são
c) Pascal – maior
aplicações do Principio de
Pascal, que garante que a
X d) Pascal – igual
e) Arquimedes – maior
pressão é a mesma em
qualquer ponto do fluido,
TEOREMA DE STEVIN
“A diferença de pressão entre dois pontos
no interior de um líquido depende do
líquido, da gravidade e da diferença de
profundidade dos pontos considerados”.
p A  p B   . g . h
TEOREMA DE STEVIN:
Aplicações
Vasos Comunicantes
Paradoxo Hidrostático:
embora as áreas sejam
diferentes, a pressão do
fluidos não depende da área
do recipiente que lhe contém,
mas sim da profundidade
Tubo em “U”
 1 .h1   2 .h 2
Exemplo
(UFSM-93) No tubo representado na figura, há dois
líquidos imiscíveis. Sabendo-se que o líquido menos
denso é a água cuja densidade vale 1,0g/cm³, a
densidade do outro líquido, em gramas por
centímetro cúbico, é:
a) 0,4
b) 1,5
c) 2,0
X d) 2,5
e) 3,0
Solução:
μ1.h1 = μ2.h2
1.10 = μ.4
μ = 2,5g/cm³
Empuxo - Arquimedes
Teorema do Empuxo
“Todo corpo mergulhado num fluido
em equilíbrio recebe deste uma força vertical,
de baixo para cima, numericamente igual ao
peso do volume de fluido deslocado.”
E   F . g .V FD
Peso aparente
E
Pap  P  E
E
P
P
PE
RESOLUÇÃO DE PROBLEMAS
Corpo livre, parado (flutuando ou
submerso) ou em MRU no fluido. Neste caso a
densidade do corpo é igual a do fluido.
Corpo descendo em MRUV. Neste caso a
densidade do corpo é maior que a do líquido.
Corpo subindo em MRUV. Neste caso a
densidade do corpo é menor que a do líquido.
Corpo tocando o fundo do recipiente.
Neste caso o peso aparente é igual, em
módulo, a normal.
Corpo pendurado em um fio com
dinamômetro. Neste caso a indicação do
dinamômetro (tração) é igual ao peso
aparente.
PE
PE
PE
Pap  N  P  E
Pap  T  P  E
Exemplo
(UFSM-92) Sabendo-se que a densidade da água é
1 g/cm³ e a do gelo é 0,9 g/cm³, qual a fração de
volume de um cubo de gelo que pode ser avistado
fora do nível da água?
X a)1/10
b)2/10
c) 4/10
d)6/10
e)8/10
Solução:
Como o gelo está em equilíbrio:
P=E
m.g = μL.g.VLD
μC.g.VC = μL.g.VLD
0,9.VC = 1.VLD
VLD/VC = 0,9 (9/10 ou 90%)
Portanto a fração emersa é 1/10 ou 10%
HIDRODINÂMICA
Estudo do movimento de fluidos
TENSÃO SUPERFICIAL
A superfície de alguns líquidos comportase como uma membrana esticada. Surge
uma força devido a diferença de moléculas
dos líquidos e gases encontrados na
superfície. Esta tensão dita superficial é
capaz de suportar objetos mais densos
que o líquido como o inseto da figura.
VISCOSIDADE
Viscosidade é o atrito interno no escoamento de um fluído.
Indica a dificuldade de escoamento do líquido.
Ex: o mel é mais viscoso que a água. É interessante
destacar que o vidro pode ser considerado um líquido muito
viscoso.
CAPILARIDADE
Capilaridade é o movimento de um líquido
em vasos capilares ou poros. Assim a
umidade que sobe na parede, alguns casos
de seiva nas plantas e a umidade que sobe
em um papel filtro, são casos de
capilaridade.
REGIMES DE ESCOAMENTO
ESCOAMENTO LAMINAR OU
CONTÍNUO
É o escoamento do fluido quando a
velocidade das partículas, em dado
ponto é constante. Ou seja, todas as n
partículas do líquido passam pelo ponto
P apresentam mesma velocidade
vetorial.
ESCOAMENTO
TURBULENTO OU VARIADO
É o escoamento em que a
velocidade das partículas, em dado
ponto, é variada no tempo.
Escoamento
turbulento
Escoamento
laminar
Exemplo
(PEIES 99) Analise as seguintes afirmações:
I- Alguns insetos conseguem pousar na superfície da água,
sendo suportados pela tensão superficial.
II- A viscosidade de um fluido é a resistência que as camadas
do fluido oferecem a seu deslocamento relativo.
III- No regime de escoamento laminar, as camadas do fluido
deslocam-se paralelamente umas às outras.
Está(ão) correta(s):
a) apenas I
b) apenas II
c) apenas III
d) apenas I e II
X e) I, II e III
Solução:
I 
II  
III  
VAZÃO OU DESCARGA
Vazão é a razão entre certa quantidade de fluido que
escoa e o intervalo de tempo para escoar. Pode ser
definido como o volume ∆V de certo fluido que passa por
uma secção S de um condutor em determinado intervalo
de tempo ∆t .
Q 
V
t
Q  v. A
Equivalências:
1m³ = 1000 = 1.000.000 cm ³
1 = 1000 cm³
1m² = 10.000 cm²
Equação da continuidade
Em tubulações em que existe um estrangulamento, a vazão é
a mesma em qualquer secção. Assim na secção de área
menor, a velocidade é maior, e onde a área é maior, a
velocidade é menor.
v 1 . A1  v 2 . A 2
Exemplos
(PEIES 97) Em um cano de 5 cm² de seção reta
ligado a um tanque, escoa água em regime
permanente. Se, em 15s, o cano despeja 0,75ℓ de
água no recipiente, então a velocidade da água
no cano é, em centímetros por segundo:
a)10-2
b)10-1
c) 100
X d)101
e)102
Solução:
Existe uma incompatibilidade
de unidades: 0,75ℓ = 750cm³.
Q = V/t = v.A
750/15 = v.5
v = 10m/s
Teorema de Bernoulli
Formas de
apresentar a
Equação de
Bernoulli
h1 
p1

p1   . gh 1 

v1 ²
2g
 .v1 ²
2
 h2 
p2


v2 ²
2g
 p 2   . gh 2 
 .v 2 ²
2
Aplicação do Teorema de Bernoulli
A
A
v
v
p
p
Na secção em que a área é menor, a velocidade é maior e a
pressão é menor.
Aplicação do Teorema de Bernoulli
A asa de um avião é construída de
forma que a velocidade do ar em
cima seja maior que embaixo. Com
efeito, a pressão embaixo é maior
que em cima, gerando uma força
maior embaixo, de tal forma que a
asa e, portanto todo o avião seja
forçado a subir.
Exemplo
(PEIES 98) Num tubo horizontal, escoa um fluido que obedece
à equação da continuidade (AV = constante) e à equação de
Bernoulli ( P + ½ μV2 = constante), onde A é a área da seção
reta do tubo, V, a velocidade de escoamento do fluido, P, a
pressão hidrostática e μ, a massa específica do fluido. Em
uma região de estrangulamento, onde a área da seção reta do
tubo se reduz à metade, a velocidade do fluido _________ e a
sua pressão _____________.
Selecione a alternativa que completa, corretamente, as
lacunas.
Solução:
a) aumenta – permanece constante
Na secção em que a área
X b) aumenta – diminui
é menor, a velocidade é
c) diminui – aumenta
maior e a pressão é
d) permanece constante – diminui
menor.
e) diminui – permanece constante