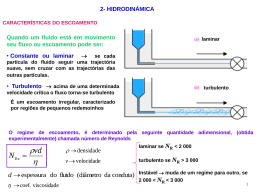
Disciplina: Mecânica dos Fluidos
Escola de Engenharia de Lorena
EEL – USP
1) CONCEITOS E PROPRIEDADES FUNDAMENTAIS DOS FLUIDOS;
2) ESTÁTICA DOS FLUIDOS;
3) CONCEITOS LIGADOS AO ESCOAMENTO DOS FLUIDOS;
4) ESCOAMENTO INCOMPRESSÍVEL DE FLUIDOS NÃO VISCOSOS;
5) ESCOAMENTO VISCOSO INCOMPRESSÍVEL.
Profa. Dra. Daniela Helena Pelegrine Guimarães
(email: [email protected])
3. CONCEITOS LIGADOS AO ESCOAMENTO DOS FLUIDOS:
 CARACTERÍSTICAS E DEFINIÇÕES DOS ESCOAMENTOS;
 EQUAÇÃO DA CONSERVAÇÃO DE MASSA;
 ESCOAMENTO LAMINAR E TURBULENTO;
 EQUAÇÃO DA CONSERVAÇÃO DE ENERGIA.
 CONCEITOS DE SISTEMA E VOLUME DE CONTROLE;
 INTRODUÇÃO Á ANÁLISE DIFERENCIAL DO MOVIMENTO DE
FLUIDOS:
 EQUAÇÃO DA CONSERVAÇÃO DE MASSA;
 EQUAÇÃO DA CONSERVAÇÃO DE Q.M.;
 EQUAÇÃO DA CONSERVAÇÃO DE ENERGIA.
I. CARACTERÍSTICAS E DEFINIÇÕES DE
ESCOAMENTO:
 DEFINIÇÃO:
- É O ESTUDO DOS CONCEITOS REFERENTES AO MOVIMENTO DOS
FLUIDOS DE UM LOCAL A OUTRO, NO INTERIOR DE UM SISTEMA DE
TRANSPORTES, EM UMA PLANTA PROCESSADORA, ONDE OS FLUIDOS
COMEÇAM A ESCOAR A PARTIR DE FORÇAS AGINDO SOBRE ELES.
RESUMINDO, É UM BALANÇO DAS FORÇAS QUE CONTRIBUEM PARA O
ESCOAMENTO E DAS QUE SE OPÕE A ESTE MOVIMENTO.

IMPORTÂNCIA:
 PROJETOS DOS EQUIPAMENTOS PROCESSADORES (BOMBAS, TANQUES,
TROCADORES DE CALOR, TUBULAÇÕES,...);
 MINIMIZA AS PERDAS DE ENERGIA NAS INDÚSTRIAS;
 EVITA UM SUB OU SUPER DIMENSIONAMENTO DOS EQUIPAMENTOS.
TROCADOR
DE
CALOR
TANQUE
FORÇAS DE INÉRICA
FORÇAS VISCOSAS
BOMBA
- FLUIDO ESCOA A PARTIR DE FORÇAS AGINDO SOBRE ELE (PRESSÃO,
GRAVIDADE, FRICÇÃO E EFEITOS TÉRMICOS): TANTO A MAGNITUDE
QUANTO A DIREÇÃO DA FORÇA QUE AGE SOBRE O FLUIDO SÃO
IMPORTANTES.
 UM BALANÇO DE FORÇAS EM UM ELEMENTO DE FLUIDO É ESSENCIAL
PARA A DETERMINAÇÃO DAS FORÇAS QUE CONTRIBUEM PARA O
ESCOAMENTO E DAS QUE SE OPÕE A ESTE MOVIMENTO.
VELOCIDADE, F. INERCIAIS, F. VISCOSAS

 TIPOS DE ESCOAMENTOS

 ENERGIABOMBEAMENTO
VISCOSIDADE ÁGUA  VISCOSIDADEÓLEO VEGETAL

 ÓLEO ESCOA M AIS LENTAM ENTE

 POTÊNCIA PARA BOMBEAR
 DESCRIÇÃO QUANTITATIVA DAS CARACTERÍSTICAS DE ESCOAMENTO DOS
FLUIDOS:
 EQUAÇÃO DA CONTINUIDADE: VELOCIDADE MÉDIA DO ESCOAMENTO
ESCOAMENTO LAMINAR
 NÚMERO DE REYNOLDS:
ESCOAMENTO TURBULENTO
 REGIMES OU MOVIMENTOS VARIADO E PERMANENTE.
VARIADO: u=f(x,y,z,t)
PERMANENTE: u=f(x,y,z)
II. EQUAÇÃO DA CONSERVAÇÃO DE MASSA:
dA2
dA1
x2
x1
X
Y
t : FLUIDO EM XX ,MOVE-SE ATÉ YY ,
X,
Y
,
- PARA QUE A MATÉRIA SEJA CONSERVADA:
MASSA EM

 
XX ,  MASSA EM YY ,
1  u1  A1  2  u2  A2
EQUAÇÃO DA CONTINUIDADE

EXEMPLO:
u ?
COMBUSTÍVEL
Q  1,8 litros
3 cm
s
EXEMPLO 2:
u ?
COMBUSTÍVEL
Q  1,8 litros
s
1,5 cm
EXEMPLO 3: Um fluido gasoso escoa em regime permanente no trecho de
tubulação da figura. Na seção (1), tem-se A1=20 cm2, 1=4 kg/m3 e U1=30
m/s . na seção (2), A2=10 cm2 e 2=12 Kg/m3. Qual é a velocidade na seção
(2)?
(1)
(2)
III. ESCOAMENTO LAMINAR E TURBULENTO:
 ESCOAMENTO LAMINAR:

m
1
 ESCOAMENTO DE TRANSIÇÃO:


m m
2
1
 ESCOAMENTO TURBULENTO:


m
3
 m1

 u  D
4m
Re 


forças vis cos as

   D
forças inerciais
 PARA ESCOAMENTO DE UM FLUIDO NO INTERIOR DE UM TUBO:
Re  2.100  ESCOAM ENTOLAM INAR
2.100 Re  4.000 TRANSIÇÃO
Re  4.000  ESCOAM ENTOTURBULENTO
 PARA ESCOAMENTO DE UM FLUIDO SOBRE UMA PLACA :
Re  500.000 ESCOAMENTOLAMINAR
Re  500.000 ESCOAMENTOTURBULENTO
EXEMPLO:
TANQUE
  1.040Kg
m3
- FLUIDO:
D  1,5 m
L  3,0 m
  1.600106 Pa s
  3 cm
BOMBA
1) QUAL O TEMPO MÍNIMO PARA ENCHER TODO O TANQUE, SOB
CONDIÇÕES DE ESCOAMENTO LAMINAR?
2) QUAL O TEMPO MÁXIMO PARA ENCHER TODO O TANQUE, SOB
CONDIÇÕES DE ESCOAMENTO TURBULENTO?
II. EQUAÇÃO DA CONSERVAÇÃO DE
ENERGIA:
C
D
P2
u2
S2
P1
A
B
u1
Z1
Z2
 S1
 INICIALMENTE UMA CERTA QUANTIDADE DO FLUIDO ESTÁ ENTRE
OS PONTOS A E C E, APÓS UM PEQUENO INTERVALO DE TEMPO t, A
MESMA
QUANTIDADE
DO
FLUIDO
MOVE-SE
PARA
OUTRA
LOCALIZAÇÃO, SITUADA ENTRE OS PONTOS B E D.
- SUPOSIÇÕES:
 ESCOAMENTO CONTÍNUO E ESTACIONÁRIO, SENDO A VAZÃO
MÁSSICA CONSTANTE;
 ENERGIAS ELÉTRICA E MAGNÉTICA SÃO DESPREZÍVEIS.
 PROPRIEDADES DO FLUIDO CONSTANTES;
 CALOR E TRABALHO DE EIXO ENTRE O FLUIDO E A VIZINHANÇA
SÃO TRANSFERIDOS À TAXA CONSTANTE.
C
D
P2
u2
S2
P1
A
B
u1
Z1
 S1
E aumento  E BD  E AC
E AC  E AB  EBC
EBD  EBC  ECD
Eaumento  EC D  EAB
Z2
EC  D
E A B
 
2
1


 m  U 2   u 2  g  z 2 
2


 
2
1


 m  U 1   u 1  g  z1 
2



 E aumento  m  U 2  U 1


1
  u2
2
  u   g  z
2
2
2
2
 z1  (*)
- MAS DE QUE MANEIRA OCORRE A TRANSFERÊNCIA DE ENERGIA
ENTRE O SISTEMA E SUAS VIZINHANÇAS ?
CALOR (Q)
TRABALHO (W)
1) COMO CALOR – ENERGIA TRANSFERIDA, RESULTANTE DA
DIFERENÇA DE TEMPERATURA ENTRA O SISTEMA E SUAS
VIZINHANÇAS.
-T.AMB.>T.S. SISTEMA RECEBE CALOR DO AMBIENTE
Q0
-T.AMB.<T.S. AMBIENTE RECEBE CALOR DO SISTEMA
Q0
2) COMO TRABALHO - ENERGIA TRANSFERIDA COMO RESULTADO
DO MOVIMENTO MECÂNICO.
SISTEMA REALIZA TRABALHO   ENERGIA DO SISTEMA
W 0
VIZINHANÇA REALIZA TRABALHO   ENERGIA DO SISTEMA
W 0
CONSIDERANDO:
E  Q  W
(**)
C
D
P2
v2
S2
P1
A
B
v1
Z1
Z2
 S1
 TRABALHO DEVE SER REALIZADO SOBRE O FLUIDO
PARA QUE ELE ENTRE NO SISTEMA;
 TRABALHO DEVE SER REALIZADO PELO FLUIDO, SOBRE
A
VIZINHANÇA, PARA QUE O FLUIDO DEIXE O
SISTEMA.
AMBOS OS TERMOS DEVEM SER INCLUÍDOS NA
EQUAÇÃO DO
BALANÇO DE ENERGIA.
 TRABALHOS DE FLUXO E DE EIXO:
- O TRABALHO LÍQUIDO, W, REALIZADO EM UM SISTEMA
ABERTO POR SUAS VIZINHANÇAS PODE SER ESCRITO
COMO:
W W W
s
W
s
W
f
 TRABALHO
f
DE EIXO, REQUER A PRESENÇA DE
DISPOSITIVO MECÂNICO (POR EXEMPLO, UMA BOMBA);
UM
 TRABALHO DE FLUXO, OU TRABALHO FEITO PELO FLUIDO NA
SAÍDA DO SISTEMA MENOS O TRABALHO FEITO SOBRE O
FLUIDO NA ENTRADA DO SISTEMA.
Wf  F  x  P  A  x
W f  P V
- ENTRADA DO SISTEMA: TRABALHO FEITO SOBRE ELE, PELO
FLUIDO LOGO ATRÁS:
W
f1
 P1 V 1
- SAÍDA DO SISTEMA: FLUIDO REALIZA TRABALHO SOBRE A
VIZINHANÇA:
W
f2
 P 2 V 2
 O TRABALHO DE FLUXO TOTAL É:
W
f
 P 2 V 2   P1 V 1
PORTANTO:
E  Q  WS  P2 V2  P1 V1
(***)
- (***)=(*):
P 1
 P 1

Qm   2   u22  g  z2    1   u12  g  z1   Ei,2  Ei,1  Wm
 2 2
  1 2



EQUAÇÃO GERAL DE ENERGIA
- PARA UM FLUIDO IDEAL, INCOMPRESSÍVEL, EM UM PROCESSO QUE
NÃO ENVOLVA TRANSFERÊNCIA DE CALOR E SEM REALIZAÇÃO DE
TRABALHO E COM A ENERGIA INTERNA DE ESCOAMENTO DO FLUIDO
PERMANECENDO CONSTANTE:
1
1
2
P1     u1    g  z1  P2     u22    g  z 2
2
2
EQUAÇÃO DE BERNOULLI
EXEMPLO
1:
ESCOAMENTO
DE
UM
FLUIDO
IDEAL
E
INCOMPRESSÍVEL ATRAVÉS DE UM BOCAL, CONFORME MOSTRADO:
DETERMINAR P1-Patm
P2=Patm
A1=0,1 m2
1
LINHA DE CORRENTE
2
V2=50 m/s
A2=0,02 m2
EXEMPLO 2: A ÁGUA ESCOA ATRAVÉS DE UM BOCAL, CONFORME
MOSTRADO, ONDE A PRESSÃO MANOMÉTRICA NO PONTO 1 É IGUAL
A 51 kPa E A VELOCIDADE 1,8 m/s. QUAIS SÃO AS VELOCIDADES E
A PRESSÃO MANOMÉTICA NO PONTO 2?
P1=51 kPa
R1=12,5 mm
1
u1=1,8 m/s
LINHA DE CORRENTE
2
R2=9,0 mm
EXEMPLO 2: UM TUBO EM U ATUA COMO UM SIFÃO DE ÁGUA. A
CURVATURA DO TUBO ESTÁ A 1 METRO ACIMA DA SUPERFÍCIE DA
ÁGUA E A SAÍDA DO TUBO ESTÁ A 7 METROS ABAIXO DA
SUPERFÍCIE DA ÁGUA. A ÁGUA SAI PELA EXTREMIDADE INFERIOR
DO SIFÃO COMO UM JATO LIVRE PARA A ATMOSFERA. DETERMINAR
A VELOCIDADE DO JATO LIVRE E A PRESSÃO ABSOLUTA MÍNIMA NA
CURVATURA.
(A)
1,0 m
(1)
8,0 m
(2)