Ensino Superior
Matemática Básica
Unidade 5 – Estudo de Funções
Amintas Paiva Afonso
O conceito de função é
um dos mais importantes
em toda a Matemática.
A idéia de função…
• Toda vez que temos
dois conjuntos e algum
tipo de associação
entre eles...
que faça corresponder a
todo elemento do
primeiro conjunto um
único elemento do
segundo, ocorre uma
função.
90
80
70
60
50
40
30
20
10
0
Leste
Oeste
Norte
1°
Trim.
3°
Trim.
Em nosso dia-a-dia temos muitos
exemplos de funções:
• O tempo de viagem é função, entre outras coisas, da
distância percorrida.
• A altura de uma criança é função de sua idade;
• O consumo de combustível é função, entre outras
coisas, da velocidade.
• Perímetro de um triângulo é função da medida de seus
lados.
O conceito de função na história...
• René Descartes (1596-1650), filósofo e matemático francês
porpôs a utilização de um sistema de eixos para localizar
pontos e representar graficamente as equações.
• Galileu Galilei (1564-1642), astrônomo e matemático
italiano iniciou o método experimental a partir do qual se
pode estabelecer uma lei que descreve relações entre as
variáveis de um fenômeno.
A função é um modo especial de relacionar
grandezas.
• Duas grandezas x e y se relacionam de tal forma que:
– x pode assumir qualquer valor em um conjunto A dado.
– a cada valor de x corresponde um único valor y em um
dado conjunto B.
– os valores que y assume dependem dos valores
assumidos por x.
Temos várias maneiras para
representar a idéia de função.
C om o rep resen tar u m a fu n çã o
d iag ram a d e setas
g rá ficos
(p lan o cartesian o)
lei d e form açã o
Representação gráfica
• No dia-a-dia
utilizamos esse tipo
de representação
em vários setores.
Algumas funções especiais:
Funções
função do prim eiro grau
função do segundo grau
o gráfico é um a reta
o gráfico é um a parábola
que pode ser
crescente
decrescente
com concavidade para cim a
com concavidade para baixo
Produto Cartesiano
A x B = { (x, y) | x  A e y  B}
A = {1, 2}; B = {2, 3, 4}
A x B = { (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4)}
Definição de função
Uma função (ou aplicação) f é uma lei segundo a
qual cada elemento x em um conjunto A está
associado a exatamente um elemento, chamado
f(x), em um conjunto B.
Definição de função através de conjuntos
Não é função de A em B
É função de A em B
Noção de função através de conjuntos
Não é função de A em B
É função de A em B
Domínio, Contradomínio e Conjunto-Imagem
Im(f)
D(f) = A
CD(f) = B
Teste da reta vertical
Para que uma curva num plano cartesiano seja gráfico de
uma função y = f(x), nenhuma reta vertical deve interceptá-la
mais de uma vez.
Domínio e imagem através do gráfico
D = {x  IR| –3  x  4 e x  1} e Im = {y  IR| –2 < y  3}
Interpretação geométrica das raízes de uma função
raiz
raiz
Seja f uma função de A em B. Denominamos raiz (ou zero)
da função f todo elemento de A para o qual temos f(x) =0.
FUNÇÃO INJETORA
É quando quaisquer dois elementos diferentes do
conjunto A têm imagens diferentes no conjunto B.
A
0
-3
4
1
6
2
8
B
Ou seja, “x” diferente
tem “y” diferente !!!
Teste da reta horizontal para verificar
se uma função é injetora
Uma função f(x) é injetora se nenhuma reta horizontal
interceptar seu gráfico em mais de um ponto.
FUNÇÃO SOBREJETORA
É quando o conjunto Imagem da função for igual ao
conjunto contradomínio. (Im = CD)
M
-1
1
1
9
3
H
Se M é o conjunto das mulheres
e H é o conjunto dos homens,
então não se pode ter homem
solteiro !!!
FUNÇÃO BIJETORA
É uma função simultaneamente injetora e sobrejetora.
Injetora: “x” diferente
tem “y” diferente
M
H
-1
1
3
5
7
9
Ou seja, homens
e mulheres com os
mesmos direitos !!
Sobrejetora: NÃO SOBRAM
elementos no contra domínio.
Injeção, sobrejeção e bijeção
a)
b)
Não é injetora.
É sobrejetora
É injetora.
Não é sobrejetora
Injeção, sobrejeção e bijeção
c)
É injetora
É sobrejetora
 É bijetora
Testando seus conhecimentos
1) Classifique as funções como bijetora, sobrejetora, injetora
ou ainda nenhuma delas:
a)
b)
4
5
6
7
1
2
3
é injetora
1
2
3
4
6
é sobrejetora
2) Classifique as funções como bijetora, sobrejetora, injetora,
ou ainda nenhuma delas:
c)
d)
1
2
3
4
5
6
é bijetora
1
2
3
3
4
5
não é sobrejetora,
nem injetora
3) Dada a função sobrejetora f : [2; 8]  B, tal que
f(x) = x² – 8x +7, observe atentamente seu gráfico e
determine seu domínio e imagem.
y
D(f) = [2;8]
Im(f) = [-9;7]
7
2
-5
-9
4
7
8
x
FUNÇÃO CRESCENTE:
f(b)
f
g
g
f
g(a)
f(a)
g(b)
f(b)
g(b)
f(a)
g(a)
O
a
b
A função f é
crescente
O
a
b
A função g é
decrescente
a
b
A função f é
crescente
a
b
A função g é
decrescente
Diz-se que f é crescente, se para a < b, então f(a) < f(b).
Diz-se que g é decrescente, se a < b então g(a) > g(b).
6) A partir da análise do gráfico, determine os intervalos
onde a função é:
y
-2
a) Decrescente:
0
2
4
]0, 4[
b) Crescente: ]-∞ ; 0[ e ]4 ; +∞[
6
x
Função crescente e Função decrescente
Função crescente e Função decrescente
Função crescente e Função decrescente
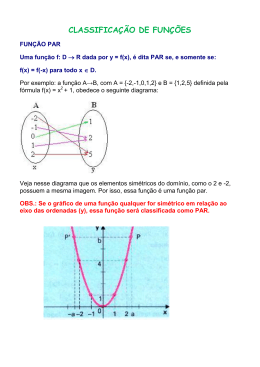
Função Par
f(x) = x4 – x2
f(-x) = (-x)4 - (-x)2 = x4 – x2 = f(x)
GRÁFICO PARA x  0
GRÁFICO COMPLETO
Os gráficos das funções pares são simétricos em relação
ao eixo das ordenadas.
Função ímpar
Gráfico para x  0
Função ímpar
f(x) = x3 + x5
f(-x) = (-x)3 + (-x)5 = -(x3 + x5) = - f(x)
Os gráficos das funções ímpares são simétricos em
relação à origem do sistema cartesiano ortogonal.
FUNÇÃO PAR:
f(x) = f(-x)
y
f(x) = x²
Uma função é PAR quando ela é
simétrica em relação ao eixo y.
Exemplo:
f(x) = x² é par pois 2² = (-2)² = 4
FUNÇÃO ÍMPAR:
f(a) = - f(-a)
x
f(x) = x³
y
Função ÍMPAR é simétrica em
relação a origem.
Exemplo:
f(x) = x³ é ímpar pois 2³ = - (-2)³
x
4) a) Verifique se f(x) = 2x³ + 5x é par ou ímpar:
Primeiro vejamos que f(1) = 2.1³ + 5.1 = 7
Em seguida, vejamos f(-1) = 2.(-1)³ + 5.(-1) = -7
Logo f(x) = 2x³ + 5x é ÍMPAR, pois f(x) = - f(-x)
ou seja, f(1) = - f(-1), pois 7 = - (-7)
b) Mostre que f(x) = 3x² é par:
Primeiro vejamos que f(1) = 3(1)² = 3
Em seguida, vejamos f(-1) = 3(-1)² = 3
Logo f(x) = x² é PAR, pois f(x) = f(-x)
ou seja, f(1) = f(-1), pois 3 = 3
5) Sendo o gráfico ao lado de f(x), o
gráfico de f(– x) será:
Lembre-se:
Se
f(x) = f(-x)
Então a função “f” é
par e ela é simétrica
ao eixo “y”.
Resposta: E
Esquema para a composição de funções
Sejam f e g duas funções quaisquer.
Denomina-se função composta de g com f a função h
definida por h(x) = g(f(x)).
FUNÇÃO INVERSA
A idéia agora é entender que y = f(x) e seguir o
seguinte procedimento:
1) Isola “x”;
2) Troca “x” por “y” e vice versa.
R
D
f(x)
x
y
f -1(x)
FUNÇÃO INVERSA
O símbolo para a função inversa de
f é f -1 e lê-se “função inversa de f”.
O símbolo “–1” em f-1 não é um expoente;
f-1(x) não significa 1/f(x).
FUNÇÃO INVERSA
TESTE DA RETA HORIZONTAL
Uma função f tem inversa se e somente se o gráfico da mesma
for cortado apenas uma vez por qualquer reta horizontal.
EXEMPLO: a função f(x) = x2 tem inversa?
y ou f(x)
y = x2
ou
f(x) = x2
reta horizontal
4
-2
0
2
x
Conclusão: a função f(x) = x2 não tem inversa.
Simetria das funções inversas
f
1.
.3
3.
.7
7.
. 15
A
B
f -1
1.
.3
3.
.7
7.
. 15
A
B
Os gráficos de f e f –1 são simétricos em relação à
bissetriz dos quadrantes ímpares (reta y = x).