Representação :
1) Um conjunto formado por números
inteiros entre 2 e 7.
A
A =
x
 Z / 2 < x < 7

4
3
A={3,4,5,6}
5
6
2) Um conjunto formado por números
A
Naturais pares e primos.
A =
x
 N / x e par e primo
A={ 2 }

2
conjunto unitário
3) Um conjunto formado por números
racionais cujo quadrado é oito .
A =

A =
 
x  Q / x2= 8
ou

A
A = 
Conjunto
Vazio
1)  ou 
Nas relações de elemento e conjunto.
Exemplos:
Seja o conjunto A = { 1 , 2 , 3 }, então :


A
7 .....
1 ..... A
3 ..... A
2)  ,  ,  , 
Nas relações de conjunto e conjunto.
Exemplos:
1) Sejam os conjuntos A = { 1 , 2 } e
B={1,2,3,4}

B
4 .....
2 ..... A

B
..... A
A ..... B
2) Seja o conjunto A = { 1 , 2, { 2 } },
então :

2
..... A
{2}
..... A

 ..... A
1 ..... A


{{ 2 }}
..... A
 A
{ 1 , 2 } .......
{ 1 } ..... A
{ 2 } ..... A

{ 1 , 2, { 2 } } .........A
1- UNIÃO : (  )
A
B
A  B
EXEMPLO :
A={1,2}
e B={2,3,4,5}
A  B = { 1 , 2 , 3, 4 , 5 }
2- INTERSEÇÃO : (  )
A
B
A  B
EXEMPLO :
A={1,2}
A
1
e B={4,5}
B
4
2
5
A  B = { }
Conjuntos
Disjuntos
3- DIFERENÇA :
A-B
B-A
B
A
A
EXEMPLO :
A={1,2,3 }
A-B={1}
B-A = {4,5 }
e B={2,3,4,5 }
B
4- COMPLEMENTAR :
A
BA
A
B
B
CAB(complementar de B em relação a A )
Obs: C B= A - B
A
EXEMPLO : A = { 1, 3 }
e B={1,2,3,4 }
CBA= { 2 , 4 }
O conjunto A tem 20 elementos, o conjunto
A  B tem 12 elementos , o conjunto A  B tem
60 elementos . O número de elementos do
conjunto B é :
a) 28
b) 36
c) 40
d) 48
e) 52
a
b
c
A
A
A B
A B
B
20 elementos
12 elementos
60 elementos
a + b = 20
b = 12
a + b + c = 60
20 + c = 60
b + c = 52
c = 40
Numa escola há n alunos. Sabe-se que 56 alunos lêem o jornal A , 21 lêem os jornais A e B,
106 lêem apenas um dos dois jornais e 66 lêem
o jornal B . O valor de n é :
a) 249
b) 137
c) 158
d) 127
e) 183
a
A
b
c
d
B
Nenhum
A
56 alunos
AeB
21 alunos
Um dos jornais
106 alunos
Não lêem o jornal B
66 alunos
a + b = 56
b = 21
a + c = 106
a + d = 66
a = 35
b = 21
c = 71
d = 31
158
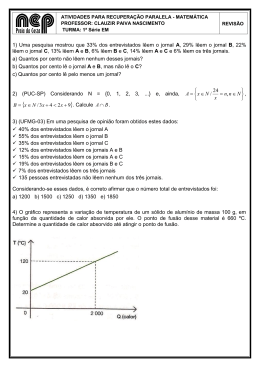
Com o objetivo de analisar o consumo de três
marcas A, B e C de um mesmo produto, faz-se uma
pesquisa em que foram consultadas 1000 pessoas.
O resultado da pesquisa encontra-se na tabela
abaixo:
Marca
A B
C A e B A e C B e C A,B,e C
Número de
400 450 520 100
Consumidores
200
300
60
Marca
A B
C A e B A e C B e C A,B,e C
Número de
400 450 520 100
Consumidores
A
200
B
40
160
110
60
140
1000 830
170
300
C
240
80
60
Um subconjunto X de números naturais contém
precisamente doze múltiplos de 4, sete múltiplos de
6, cinco múltiplos de 12 e oito números ímpares.
O número de elementos de X é :
a) 32
b) 27
c) 24
d) 22
a
b
c
M(4)
8
M(6)
ímpares
M(12)
a + b = 12
b+c=7
a=7
c=2
b=5
Total = 7 + 5 + 2 + 8 = 22
Num conjunto de 30 pessoas, 5 são altas e gordas
11 são baixas e 13 são goras .
a) Quantas são altas e magras ?
b) Quantas são baixas e magras ?
Altas
a
Baixas
Gordas Gordas
b
c
a + b + c +d = 30
a = 14
b=5
c + d = 11
d=3
b + c = 13
c=8
d
Altas e Magras
14
Baixas e Magras
3
Passei todos os dias de minhas férias no litoral brasileiro.
Quando eu ia à praia pela manhã, não ia à tarde. Fui à
praia 10 dias, tendo perdido 6 manhãs e 8 tardes de praia.
Quantos dias duraram minhas férias ?
a) 12
b) 14
c) 16
d) 24
Manhã
6
Tarde
Praia
x
8
10 - x
6 + x = 18 - x
2 x = 12
x=6
Total de dias = 12