Colégio Adventista de Telemaco Borba

Pode-se associar conjunto à ideia relacionada
uma coleção qualquer de objetos, itens ou
grupo de pessoas.



No ensino fundamental, estudamos
procedimentos para encontrar raízes de
equações de primeiro e segundo grau.
Essas raízes podem ser representadas por um
conjunto-solução.
Ex:
x2 – 5x + 6 = 0
Logo temos, x’ = 2 e x’’ = 3

S

S = { 2 , 3}
2
3
Diagrama
Entre chaves
Propriedade

S = { x / x é solução da equação x2 – 5x + 6 = 0}

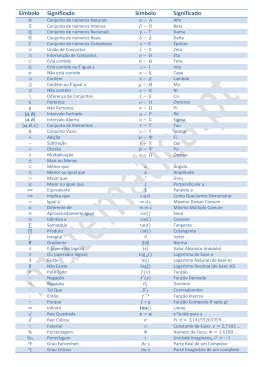
∈ (pertence) e ∉ (ñ pertence) – elementos
associados ao conjunto.


Dois conjuntos podem estar associados. Para
tanto, usamos os símbolos ⊂(está contido) e
⊄(ñ está contido) ou ⊃(contém) e ⊅(ñ contém).
Ex:
Ex:
A
A
B
A⊄Be B⊂A
A⊃BeB⊅A
B
Nessa representação, o
conjunto B não está
contido em A.

Conjunto universo é o conjunto ao qual
pertencem todos os elementos do contexto em
estudo. Pode também ser definido como sendo
o conjunto formado por todos os valores que
a(s) variável(is) pode(m) assumir.


Um conjunto é vazio quando não possui
elemento algum.
Para representá-lo, existem duas maneiras: { }
ou ⌀.
Para você fazer:
Em sua cidade, defina um conjunto A qualquer do
qual você faça parte como membro. Em seguida,
defina um subconjunto B contido em A, do qual
você não faça parte:

Um conjunto unitário é constituído de um
único elemento.

(
(
(
(
(
(
(
(
Dadas as afirmações a seguir, marque V para verdadeira e F para falsa:
) Se A = {m, n, p, q}, então m ∈ A.
) {2, 3} ⊂ {2, 3, 4}
) {0, 2, 4, 6, ...} ⊂ {0, 1, 2, 3, 4, 5, 6, ...}
) Se A ⊂ B e B ⊂ C, então A ⊂ C.
) ⌀ ⊂ A, qualquer que seja A.
) {x} = x
) Se A ⊂ B e B ⊂ A, então A = B.
) Se A = {x/x é maior que 4}, então A = {5, 6, 7, 8, ...}.
∪ - União
 ∩ - Intersecção
Ex: Considere os conjuntos A = {1, 2, 4} e B = {2, 3,
4, 5}. Vamos encontrar A ∪ B e A ∩ B.
Elementos de

A ou B.
A ∪ B = {1, 2, 4} ∪ {2, 3, 4, 5} = {1, 2, 3, 4, 5}
A ∩ B = {1, 2, 4} ∩ {2, 3, 4, 5} = {2, 4}
Elementos de A e B.
Dados dois conjuntos, A e B, não vazios, temos:
A ∪ B = {x/x ∈ A ou x ∈ B}
A ∩ B = {x/x ∈ A e x ∈ B}
Diagrama: A = {1, 2, 4} e B = {2, 3, 4, 5}

A
3
2
1
4
5
B