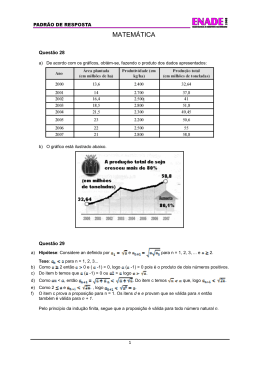
Prof. M.Sc. Carlos Alberto Bezerra e Silva
1
Material de apoio à disciplina Geometria Analítica
Produto vetorial ou externo
Ilustração da regra da “mão direita”
Na Física se usa também a regra da mão esquerda
01 Efetuar:
a) (i x k) x (i x j) =
b) (i x k) x (k x j) x (j x j) =
02 Conhecidos u = 2i + 3j + k e v = i - j + 2k, pede-se:
a) u x v
b) v x u
c) | u x v
d) | v x u |
03 Determinar o vetor unitário n, ortogonal aos vetores u = (2, 3, -1) e v = (1, 1, 2).
04 Achar o vetor w = (x, y, z), tal que w . (1, 0, 2) = 3 e w x (1, 0, -1) = (-2, 3, -2).
05 Calcular o | u |, conhecendo-se | u x v | =
06 O vetor w tem módulo 7, forma um ângulo agudo com o eixo das abscissas e é ortogonal aos
vetores
Pede-se w.
07 Determinar um vetor concomitantemente perpendicular aos vetores u + v e 2v - u, sendo u = i + j
e v = 2i – k.
ÁLGEBRA VETORIAL E GEOMETRIA ANALÍTICA - Jacir. J. Venturi©
Prof. M.Sc. Carlos Alberto Bezerra e Silva
2
08 Representar no triedro positivo i, j e k:
a) a = (2 j ) x (3 i )
c) c = (2 j ) x k
b) b = i x (3k )
09 Calcular o vetor de módulo 18 e simultaneamente ortogonal a u = (2, -1, 0) e a v = (2, - 4, 3).
10 Sendo v = (1, - 1, 1), calcular o(s) vetor(es) u = (x, y, z) que satisfaça (m) as três condições
seguintes:
1) u seja ortogonal ao eixo x;
2) u . v = 0;
3) | v x u | =
11 Sendo | u | = 5, | v | = 2 e u . v = 8. Calcular | u x v |.
12 Na figura abaixo obter:
u.v+u.w+v.w+|vxw|
13 Num hexágono regular, a medida de cada lado vale 2. Calcular |(A - B) x (C – B)|.
14 Seja um plano determinado pelos vetores u = (2, -1, 0) e v = (0, 1, -1). Determinar o conjunto de
vetores ortogonais a . α
15 Sendo | u | = 4, | v | = 3 e uv = 150 , calcular:
a) a área do triângulo construído sobre u e v;
b) a área do paralelogramo construído sobre u + v e 2u – 3v
16 Pede-se a área o paralelogramo construído sobre u + 2v e u - v,
ÁLGEBRA VETORIAL E GEOMETRIA ANALÍTICA - Jacir. J. Venturi©
Prof. M.Sc. Carlos Alberto Bezerra e Silva
3
sendo | u | = 4, | v | = 3 e uv = 120º
17 Provar que a área do paralelogramo construído sobre a + b e a - b é o dobro da área do
paralelogramo construído sobre a e b.
18 Calcular a área do triângulo construído sobre u = 2i - j + k e v = - i + j – k.
19 A área de um
Pede-se o valor de a.
paralelogramo construído sobre u = (1, 1, a) e v = (-1, 1, 0) é igual a
20 Determinar a área do paralelogramo construído sobre u e v cujas diagonais são
21 No triângulo de vértices A = (0, 0, 2), B = (3, - 2, 8) e C = (- 3, - 5, 10), calcular:
a) a medida dos lados a, b, c;
b) a medida dos ângulos A, B, C;
c) a área do triângulo.
22 Os pontos (3, 1, 1), (1, -2, 3), (2, -1, 0) são os pontos médios dos lados do triângulo ABC. Qual a
área do triângulo ABC?
23 Calcular a altura relativa ao vértice B do triângulo de vértices A=(2, 4, 0), B=(0, 2, 4) e
C=(6, 0, 2).
24 Demonstrar a lei dos senos.
25 Achar a área do quadrilátero A = (1, 4, 0), B = (5, -1, 0), C = (0, -1, 0) e D = (- 4, 2, 0).
ÁLGEBRA VETORIAL E GEOMETRIA ANALÍTICA - Jacir. J. Venturi©