UNIVERSIDADE FEDERAL DA BAHIA
ESCOLA POLITÉCNICA
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA
Dissertação de Mestrado
Análise e Previsão da Volatilidade do Preço de
Liquidação das Diferenças no Mercado Brasileiro
Utilizando o Modelo GARCH
ANTÔNIO JOSÉ SOBRINHO DE SOUSA
Salvador – Bahia – Brasil
©Antônio José Sobrinho de Sousa, Agosto de 2013.
S725
Sousa, Antônio José Sobrinho de
Análise e previsão da volatilidade do preço de liquidação
das diferenças no mercado brasileiro utilizando o modelo
GARCH / Antônio José Sobrinho de Sousa. – Salvador, 2013.
100 f. : il. color.
Orientador: Prof. Doutor André Luiz de Carvalho Valente
Dissertação (mestrado) – Universidade Federal da Bahia.
Escola Politécnica, 2013.
1. Energia elétrica. 2. Política de preços. Métodos de
simulação. I. Valente, André Luiz de Carvalho. II. Universidade
Federal da Bahia. III. Título.
CDD: 621.31
Antônio José Sobrinho de Sousa
Análise e Previsão da Volatilidade do Preço de
Liquidação das Diferenças no Mercado Brasileiro
Utilizando o Modelo GARCH
Dissertação apresentada à Coordenação do Programa de
Pós-Graduação em Engenharia Elétrica da Universidade
Federal da Bahia, em cumprimento às exigências para
obtenção do Grau de Mestre em Engenharia Elétrica.
André Luiz de Carvalho Valente, D.Sc.
Orientador
Salvador – Bahia
Agosto de 2013
Antônio José Sobrinho de Sousa
Análise e Previsão da Volatilidade do Preço de
Liquidação das Diferenças no Mercado Brasileiro
Utilizando o Modelo GARCH
Dissertação de mestrado aprovada como parte dos requisitos para obtenção do grau de
Mestre em Engenharia Elétrica do curso de Pós-Graduação em Engenharia Elétrica da
Universidade Federal da Bahia.
Banca Examinadora:
Orientador:
_____________________________________________
Prof. Dr. André Luiz de Carvalho Valente
UFBA
Membro:
_____________________________________________
Prof. Dr. Paulo Roberto Ferreira de Moura Bastos
UFBA
Membro:
_____________________________________________
Prof. Dr. Osvaldo Livio Soliano Pereira
UNIJORGE
Salvador, Bahia, 05 de Agosto de 2013.
À minha mãe Noélia, meus filhos Lucas e Rafael, à Isa pelo
incansável apoio, e a todos os meus familiares e amigos por
minha ausência e dispersão.
Agradecimentos
Agradeço primeiramente a Deus, a toda minha família, em especial a minha mãe
Noélia Alvares Sobrinho Gonçalves, que sempre com carinho e atenção me apoiou. A meu
pai, Firmino de Sousa (In Memoriam), com a sua retidão e inteligência balizaram minha
vida. Aos meus amados filhos Lucas e Rafael para quem dedico especialmente esta vitória.
A minha noiva, Isa e meus enteados Matheus e André que com muito amor, dedicação
suporte e compreensão proporcionaram-me também um porto seguro para esta grande
empreitada.
Agradeço à Universidade Federal da Bahia e ao Departamento de Engenharia
Elétrica pelo apoio e infraestrutura concedidos para exercer meus estudos. A todos os
professores do programa de pós-graduação em engenharia elétrica pelos ensinamentos que
me foram passados, em especial ao professor André Luiz de Carvalho Valente pela formal
orientação, e por ajudar de forma incondicional no desenvolvimento desta dissertação.
Aos professores Fernando Augusto Moreira, Caiuby Alves Costa e Niraldo Roberto
Ferreira pela contribuição e participação valiosa no suporte e na infraestrutura durante este
curso de mestrado. Complemento também aos professores Paulo Roberto Ferreira de
Moura Bastos e Humberto Xavier de Araújo pelo apoio e sugestões inclusos neste trabalho.
Meus sinceros agradecimentos a CAPES pela concessão da bolsa de estudos.
Agradeço a meus colegas de jornada: Eduardo Andrade, Omar Alexander Chura
Vilcanqui, Huilman Sanca Sanca, Leroy Umasi, Cesar Peña, Miguel Pereira Neto, Roniere
da Silva, Wilton Lacerda, Carolina Moreno, Betânia Gomes da Silva Filha e também a
todos os amigos que contribuíram, ainda que de forma inconsciente, para a conclusão deste
trabalho, sendo eles companheiros tanto nos momentos de dificuldade quanto também nos
momentos de descontração.
SOUSA, Antônio J. Sobrinho de. Análise e Previsão da Volatilidade do Preço de Liquidação das
Diferenças no Mercado Brasileiro Utilizando o Modelo GARCH. 100 f. 2013. Dissertação (Mestrado em
Engenharia Elétrica) – Escola Politécnica, Universidade Federal da Bahia, Salvador, Brasil, 2013.
Resumo
Neste trabalho o escopo está concentrado na análise da volatilidade1 dos preços da
energia elétrica no mercado à vista, ou seja, spot, tendo como base uma série temporal
univariada do Preço de Liquidação das Diferenças (PLD) semanal comercializados na
Câmara de Comercialização de Energia Elétrica (CCEE). Sendo esta série utilizada em
modelos GARCH2 no objetivo que capturem e representem a volatilidade e possibilitem
gerar previsões complementares a esta série.
Após esta introdução apresenta-se a revisão bibliográfica onde são expostos os
principais trabalhos relacionados com o assunto. Em seguida expõe-se a fundamentação
teórica, contendo os principais fundamentos, procedimentos e condições de previsões do
respectivo modelo utilizado em séries temporais, bem como modelos, ajustes nos modelos
de previsão que consigam representar a volatilidade. A metodologia de Box-Jenkins foi
utilizada para as simulações conjuntamente com os procedimentos de verificação e testes
no objetivo de definir o modelo mais adequado a série temporal. Sendo implementados os
algoritmos e obtidos os resultados nos softwares R e EViews.
Complementarmente na análise dos resultados se efetuou comparações entre os
algoritmos, entre os valores das previsões e os valores reais e verificação da correlação.
Visando sempre obter resultados que agregassem melhorias as previsões.
A conclusão do trabalho comprova a existência de altíssima volatilidade dos preços
de energia elétrica no mercado brasileiro, bem como avalia a eficácia da utilização do
modelo GARCH para análise e previsões neste ambiente.
Encerrando este trabalho são abordados temas e sugestões para futuros
desenvolvimentos, objetivando contribuir para um novo patamar a ser alcançado após as
análises aqui exploradas.
Palavras-Chaves: GARCH, Volatilidade, Simulação, Energia Elétrica, CCEE.
1
2
Grau de variação imprevisível de uma determinada variável, representa incerteza e risco.
Modelo Auto-Regressivo Generalizado de Heterocedasticidade Condicional.
SOUSA, Antônio J. Sobrinho de. Analysis and Forecasting of Price Volatility Settlement of Differences in
the Brazilian Market Using GARCH Model. 100 f. 2013. Dissertation (Masters in Electrical Engineering) –
Federal University of Bahia, Salvador, Brazil, 2013.
Abstract
In this work, the scope is focused on the analysis of the volatility of energy prices
on the spot market, based on a time series of univariate Price Settlement of Differences
(PLD) weekly marketed in the Chamber of Electric Energy Commercialization (CCEE). In
this series, GARCH models are used in order to capture and represent the volatility and
generate forecasts that allow complementary forecasts to this series.
After this introduction, a literature review is presented where the main works
related to the subject are exposed. In sequence, the theoretical background is presented,
containing the main principles, procedures and conditions of the respective model
predictions used in time series, as well as, models and adjustments in forecast models that
are able to represent volatility. The method of Box-Jenkins was used in the simulations
together with verification procedures and tests with the purpose of defining an adequate
model to the time series. The algorithms were implemented and the results obtained in the
softwares R and EViews.
In Addition, in the analysis of the results, comparisons among the algorithms were
performed between the forecasted and real values and the correlation has been verified
with the purpose of obtaining results that may improve the forecasts.
The conclusion of this work proves the high volatility of electric energy prices in
the Brazilian market, as well as, evaluates the efficiency of using the GARCH model for
analysis and forecasts in this environment.
In the end of this work, themes and suggestions for future developments are
discussed with the purpose contributing to a new level to be reached after the analysis here
presented.
Keywords: GARCH, Volatility, Simulation, Energy, CCEE.
viii
Glossário
ACF
Autocorrelation Function
ACL
Ambiente de Contratação Livre
ADF
Argumented Dickey-Fuller
AIC
Akaike Information criterion
ANEEL
Agência Nacional de Energia Elétrica
AR
Auto-Regressive
ARCH
Auto-Regressive Conditional Heteroscedasticity
ARIMA
Auto-Regressive Integrated Moving Average
ARMA
Auto-Regressive Moving Average
CAPES
Coordenação de Aperfeiçoamento de Pessoal de Nível Superior
CCEAL
Câmara de Comercialização de Energia Elétrica no Ambiente Livre
CCEAR
Contrato de Comercialização de Energia no Ambiente Regulado
CCEE
Câmara de Comercialização de Energia Elétrica
CEPEL
Centro de Pesquisas de Energia Elétrica
CMG
Custo Marginal de Geração
CMO
Custo Marginal de Operação
CP
Confecção Própria com dados da CCEE
EWMA
Exponentially Weighted Moving Average
FCF
Função de Custo Futuro
FCI
Função de Custo Imediato
FDP
Função Densidade de Probabilidade
GARCH
Generalized Auto-Regressive Conditional Heteroscedasticity
GJR
Glosten-Jagannathan-Runkle
HQC
Hannan-Quinn Criterion
i.i.d
Independente e identicamente distribuído
JB
Jarque-Bera Test
LB
Ljung-Box Test
LLF
Log-Likelihood Function
MA
Moving Average
ix
MAD
Mean Absolute Deviation
MAE
Mean Absolute Error
MAE
Mercado Atacadista de Energia
MAPE
Mean Absolute Percentage Error
MCSD
Mecanismo de Compensação de Sobras e Déficits
MGB
Movimento Geométrico Browniano
MMS
Médias Móveis Simples
MRE
Mecanismo de Realocação de Energia
MSE
Modelo de Suavização Exponencial
MWh
Mega Watts hora
NE
Região Nordeste
ONS
Operador Nacional do Sistema
PACF
Partial Autocorrelation Function
PCH
Pequena Central Hidroelétrica
PE
Processo Estocástico
PLD
Preço de Liquidação das Diferenças
QGARCH
Quadratic Generalized Auto-Regressive Conditional Heteroscedasticity
RMSE
Root Mean Square Error
SARIMA
Seasonal Auto-Regressive Integrated Moving Average
s.e.
Standard Error
SEB
Setor Elétrico Brasileiro
SECO
Região Sudeste/Centro-Oeste
SES
Simple Exponential Smoothing
SIC
Schwartz Information Criterion
SIN
Sistema Interligado Nacional
SO
Sem Outliers
ST
Série Temporal
v.a.
Variável Aleatória
VR
Valor de Referência
x
Lista de Figuras
Figura 1 – Variações de Preços da Commodity Energia Elétrica (CP) ............................... 10
Figura 2 – Gráficos de Variações de Preços de Commodities............................................ 10
Figura 3 – Evolução do PLD Patamar Pesado por Região (CP) ........................................ 10
Figura 4 – Retorno Simples do PLD Região SE/CO Patamar Pesado (CP) ....................... 11
Figura 5 – Gráficos de Evolução do PLD por Região – Patamar Pesado (CP) ................... 11
Figura 6 – Sobreposição do Preço e Log-Retorno do PLD de Energia Elétrica (CP) ......... 12
Figura 7 – Estrutura de Comercialização do SEB. ............................................................ 13
Figura 8 – Fluxograma de Operação de um Sistema Hidrotérmico. ..................................17
Figura 9 – Funções de Custos ........................................................................................... 18
Figura 10 – Curva de Oferta e Demanda e Custo Marginal de Operação........................... 19
Figura 11 – Processo estocástico visto como uma família de variáveis aleatórias. ............. 29
Figura 12 – Um processo estocástico interpretado como uma família de trajetórias. ......... 30
Figura 13 – Tipos de Tendências de uma Série Temporal ................................................. 31
Figura 14 – Padrão Cíclico em torno de 10 ou 11 anos ..................................................... 31
Figura 15 – Tendência e Sazonalidade ............................................................................. 31
Figura 16 – Variação Irregular em 1915 ........................................................................... 32
Figura 17 – Homocedasticidade ....................................................................................... 33
Figura 18 – Heterocedasticidade ...................................................................................... 34
Figura 19 – Distribuição hipotética das alturas dos filhos em relação às alturas dos pais...41
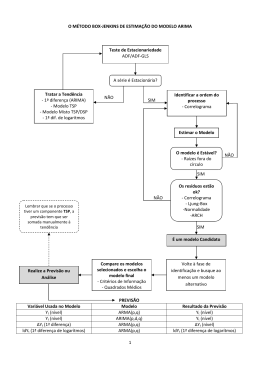
Figura 20 – Método de Box-Jenkins (CP)......................................................................... 52
Figura 21 – Evolução do PLD Região SE/CO, Período de 2005 a 2010 (CP) .................... 54
Figura 22 – Retornos da Série Temporal SE/CO de 2005 a 2010 (CP) .............................. 55
Figura 23 – Histograma da Série Temporal SE/CO de 2005 a 2010 (CP) .......................... 55
Figura 24 – Função Densidade, ACF e PACF dos Retornos (CP) .....................................56
Figura 25 – Resíduos estandardizados, ACF e Teste Ljung-Box – ARIMA(2,0,2) (CP)....57
Figura 26 – ACF e PACF dos quadrados dos resíduos – ARIMA(2,0,2) (CP)................... 58
Figura 27 – Resíduos dos Retornos do Modelo GARCH(1,1) / ARIMA(2,0,2) (CP)......... 59
Figura 28 – ACF, PACF e Histograma de uma ST de Volatilidade Comportada (CP) ....... 59
xi
Figura 29 – ACF, PACF e Histograma dos Resíduos GARCH(1,1)/ARIMA(2,0,2) (CP)..60
Figura 30 – Gráfico de Previsão do PLD Modelo GARCH(1,1) / ARIMA(2,0,2) (CP) .....60
Figura 31 – Resíduos estandardizados, ACF e Teste Ljung-Box – ARIMA(4,0,4) (CP)....61
Figura 32 – ACF e PACF dos quadrados dos resíduos – ARIMA(4,0,4) (CP)................... 61
Figura 33 – Resíduos dos Retornos do Modelo GARCH(1,1) / ARIMA(4,0,4) (CP)......... 62
Figura 34 – ACF, PACF e Histograma dos Resíduos GARCH(1,1)/ARIMA(4,0,4) (CP)..63
Figura 35 – Gráfico de Previsão do PLD Modelo GARCH(1,1) / ARIMA(4,0,4) (CP) .....63
Figura 36 – Gráfico da Série Temporal do PLD Sem Outliers (CP) ..................................64
Figura 37 – Gráfico dos Retornos do PLD Sem Outliers (CP) .......................................... 64
Figura 38 – Histograma dos Retornos do PLD Sem Outliers (CP) ....................................65
Figura 39 – Densidade, ACF e PACF dos Retornos do PLD Sem Outliers (CP) ............... 65
Figura 40 – Gráfico de Previsão Modelo GARCH(1,1) / ARIMA(1,0,1) Sem Outliers .....67
Figura 41 – Gráfico de Previsão Modelo GARCH(1,1) / ARIMA(2,0,2) Sem Outliers ....68
Figura 42 – Evolução do PLD Região SE/CO, Período de 2005 a 2010 (CP) .................... 70
Figura 43 – Estatísticas ACF e PACF de SE/CO (CP) ..................................................... 70
Figura 44 – Gráfico da Transformação ou Retornos da ST SE/CO (CP) ........................... 71
Figura 45 – Histograma dos Retornos de SE/CO (CP) ...................................................... 71
Figura 46 – Gráfico de Previsão Modelo GARCH(1,1) da ST do PLD (CP) ..................... 72
Figura 47 – Gráficos de Previsões GARCH(1,1) e Estatísticas (CP) .................................72
Figura 48 – Evolução do PLD Região SE/CO, Período 2005 a 2010 Sem Outliers (CP) ...73
Figura 49 – Retornos do PLD Região SE/CO, Período 2005 a 2010 Sem Outliers (CP)....73
Figura 50 – Histograma dos Retornos de SE/CO Sem Outliers (CP).................................74
Figura 51 – Gráfico de Previsão Modelo GARCH(1,1) da ST do PLD Sem Outliers (CP) 74
Figura 52 – Gráficos de Previsões GARCH(1,1) e Estatísticas Sem Outliers (CP)............ 75
xii
Lista de Tabelas
Tabela 1 – Substituição de Valores Considerados Outliers ............................................... 37
Tabela 2 – Sumário Estatístico da Série Temporal do PLD no R®(CP) ............................. 54
Tabela 3 – Coeficientes Estimados dos Modelos ARIMA da ST do PLD (CP) ................. 56
Tabela 4 – Resumo de Coeficientes e Critérios dos Modelos ARIMA Estimados ............. 57
Tabela 5 – Estimação GARCH do Modelo ARIMA(2,0,2) Ajustado ................................ 58
Tabela 6 – Testes JB e LB da Estimação GARCH do Modelo ARIMA(2,0,2) Ajustado ...59
Tabela 7 – Estimação GARCH do Modelo ARIMA(4,0,4) Ajustado ................................ 62
Tabela 8 – Testes JB e LB da Estimação GARCH do Modelo ARIMA(4,0,4) Ajustado ...62
Tabela 9 – Sumário Estatístico da ST do PLD no R® – Sem Outliers (CP) ....................... 64
Tabela 10 – Coeficientes Estimados dos Modelos ARIMA(1,0,0) a (4,0,4) Sem Outliers .66
Tabela 11 – Resumo de Coeficientes e Critérios dos Modelos ARIMA – Sem Outliers ....66
Tabela 12 – Estimação GARCH do Modelo ARIMA(1,0,1) – Sem Outliers..................... 67
Tabela 13 – Testes JB e LB da Estimação GARCH / ARIMA(1,0,1) – Sem Outliers........ 67
Tabela 14 – Estimação GARCH do Modelo ARIMA(2,0,2) – Sem Outliers..................... 68
Tabela 15 – Testes JB e LB da Estimação GARCH / ARIMA(2,0,2) – Sem Outliers........ 68
Tabela 16 – Estimação GARCH do Modelo ARIMA(4,0,4) – Sem Outliers..................... 69
Tabela 17 – Testes JB e LB da Estimação GARCH / ARIMA(4,0,4) – Sem Outliers........ 69
Tabela 18 – Sumário Estatístico da Série Temporal do PLD no Eviews®(CP)................... 69
Tabela 19 – Critérios para escolha do modelo GARCH (CP) ............................................ 71
Tabela 20 – Critérios para escolha do modelo GARCH – Sem Outliers (CP) ................... 74
Tabela 21 – Estimativas de Erros de Previsão (CP) .......................................................... 75
xiii
Lista de Equações
(1) ....................................................................................................................................25
(2) ....................................................................................................................................26
(3) ....................................................................................................................................32
(4) ....................................................................................................................................33
(5) ....................................................................................................................................33
(6) ....................................................................................................................................35
(7) ....................................................................................................................................35
(8) ....................................................................................................................................35
(9) ....................................................................................................................................35
(10) ..................................................................................................................................35
(11) ..................................................................................................................................39
(12) ..................................................................................................................................39
(13) ..................................................................................................................................40
(14) ..................................................................................................................................42
(15) ..................................................................................................................................42
(16) ..................................................................................................................................43
(17) ..................................................................................................................................45
(18) ..................................................................................................................................45
(19)..................................................................................................................................46
(20) ..................................................................................................................................46
(21) ..................................................................................................................................47
(22) ..................................................................................................................................47
(23) ..................................................................................................................................47
(24) ..................................................................................................................................47
(25) ..................................................................................................................................48
(26) ..................................................................................................................................48
(27) ..................................................................................................................................49
(28) ..................................................................................................................................49
(29) ..................................................................................................................................49
(30) ..................................................................................................................................49
(31) ..................................................................................................................................50
(32) ..................................................................................................................................50
(33) ..................................................................................................................................50
(34) ..................................................................................................................................55
SUMÁRIO
I
SUMÁRIO
GLOSSÁRIO ......................................................................................................... VIII
LISTA DE FIGURAS ................................................................................................ X
LISTA DE TABELAS............................................................................................. XII
LISTA DE EQUAÇÕES ........................................................................................ XIII
SUMÁRIO ................................................................................................................... I
1. INTRODUÇÃO ...................................................................................................... 3
1.1. JUSTIFICATIVA .............................................................................................. 3
1.2. DESCRIÇÃO DO PROBLEMA ........................................................................ 3
1.3. OBJETIVO PRINCIPAL ................................................................................... 3
1.4. OBJETIVOS ESPECÍFICOS ............................................................................. 4
1.5. RESULTADOS ESPERADOS .......................................................................... 5
1.6. DELIMITAÇÕES DO TRABALHO ................................................................. 5
1.7. ORGANIZAÇÃO DO TEXTO .......................................................................... 6
2. O SETOR ELÉTRICO BRASILEIRO ................................................................. 7
2.1. BREVE HISTÓRICO ........................................................................................ 7
2.2. ACR E ACL ...................................................................................................... 7
2.2.1. ACR ....................................................................................................... 8
2.2.2. ACL ....................................................................................................... 8
2.3. SINGULARIDADE E VOLATILIDADE .......................................................... 9
2.4. A PRECIFICAÇÃO E RISCO ......................................................................... 12
2.5. IMPACTOS NOS AGENTES .......................................................................... 12
2.5.1. Geração ............................................................................................... 13
2.5.2. Distribuição ......................................................................................... 14
2.5.3. Comercialização .................................................................................. 15
2.5.4. Consumidores Livres ........................................................................... 16
2.5.5. Importadores e Exportadores .............................................................. 16
2.6. MITIGAÇÃO DE RISCOS NO AMBIENTE DE ENERGIA ELÉTRICA ........ 16
2.6.1. Preço de Liquidação das Diferenças – PLD ........................................ 19
2.6.2. Formas de Mitigação de Riscos ........................................................... 20
2.6.3. Mecanismo de Realocação de Energia – MRE.................................... 20
2.6.4. Mecanismo de Compensação de Sobras e Déficits – MCSD ............... 21
2.6.5. Derivativos de Energia Elétrica ........................................................... 21
3. REVISÃO BIBLIOGRÁFICA ............................................................................. 23
3.1. MODELO ARMA – (1960) ............................................................................. 24
3.2. MÉTODO DE BOX-JENKINS – (1970) .......................................................... 24
3.3. MODELO ARIMA – (1976) ............................................................................ 24
3.4. MODELO – SARIMA – (1976) ....................................................................... 25
3.5. MODELO DE ENGLE – ARCH – (1982) ........................................................ 25
3.6. MODELO DE BOLLERSLEV – GARCH – (1986).......................................... 26
4. FUNDAMENTAÇÃO TEÓRICA........................................................................ 27
4.1. SÉRIES TEMPORAIS..................................................................................... 27
4.1.1. Tipos de Modelos ................................................................................. 28
4.1.2. Componentes Básicas .......................................................................... 30
4.1.3. Transformações ................................................................................... 34
4.1.4. Dados Discrepantes ou Outliers .......................................................... 36
SUMÁRIO
II
4.2. MODELOS DE PREVISÃO ............................................................................ 37
4.2.1. Modelos Lineares ................................................................................ 38
4.2.1.1. Modelos de Erro ou Regressão ........................................................ 39
4.2.1.2. Modelos de Suavização Exponencial – MSE .................................. 40
4.2.1.3. Modelo de Médias Móveis – MA (Moving Average)........................ 40
4.2.1.4. Modelo Auto-Regressivo – AR ........................................................ 41
4.2.1.5. Modelo Auto-Regressivo de Médias Móveis – ARMA ..................... 42
4.2.1.6. Modelo AR Integrado de Média Móvel – ARIMA ........................... 42
4.2.2. Modelos Não-Lineares ........................................................................ 43
4.2.3. Modelos ARCH e GARCH .................................................................. 44
4.2.3.1. Modelo AR de Heterocedasticidade Condicional – ARCH .............. 44
4.2.3.2. Modelo Generalizado ARCH – GARCH ......................................... 45
4.3. CRITÉRIOS DE AVALIAÇÃO E ERROS ...................................................... 46
4.3.1. Critérios de Avaliação – AIC, JB, LB e ADF ...................................... 47
4.3.1.1. Akaike Information Criterion – AIC ............................................... 47
4.3.1.2. Schwartz Information Criterion – SIC ............................................ 47
4.3.1.3. Hannan-Quinn Criterion – HQC .................................................... 47
4.3.1.4. Jarque-Bera – JB ............................................................................ 47
4.3.1.5. Ljung-Box – LB .............................................................................. 48
4.3.1.6. Teste Dickey-Fuller Aumentado – ADF .......................................... 48
4.3.2. Critérios de Erros: RMSE, MAPE, MAE ............................................ 49
4.3.2.1. Root Mean Square Error – RMSE .................................................. 50
4.3.2.2. Mean Absolute Percentage Error – MAPE ..................................... 50
4.3.2.3. Mean Absolute Error – MAE .......................................................... 50
5. METODOLOGIA PARA AS PREVISÕES E SIMULAÇÕES .......................... 51
5.1. IDENTIFICAÇÃO .......................................................................................... 53
5.2. ESTIMAÇÃO ................................................................................................. 53
5.3. VERIFICAÇÃO .............................................................................................. 53
5.4. PREVISÃO ..................................................................................................... 53
6. RESULTADOS OBTIDOS .................................................................................. 54
6.1. RESULTADOS OBTIDOS NO R® .................................................................. 54
6.1.1. Conjunto de modelos ARIMA(1,0,0) a (4,0,4) ..................................... 56
6.1.2. Ajuste do GARCH com base no ARIMA(2,0,2) ................................... 57
6.1.3. Ajuste do GARCH com base no ARIMA(4,0,4) ................................... 61
6.1.4. Resultados Obtidos Sem Outliers......................................................... 64
6.1.5. Conjunto de modelos ARIMA(1,0,0) a (4,0,4) – Sem Outliers ............. 66
6.1.6. Ajuste do GARCH com base no ARIMA – Sem Outliers ..................... 67
6.2. RESULTADOS OBTIDOS NO EVIEWS® ...................................................... 69
6.2.1. Resultados Obtidos Sem Outliers......................................................... 73
6.3. ERROS DE PREVISÃO .................................................................................. 75
7. CONCLUSÕES .................................................................................................... 76
8. DIVULGAÇÃO DA PESQUISA ......................................................................... 77
9. SUGESTÕES PARA TRABALHOS FUTUROS ................................................ 78
10.
REFERÊNCIAS BIBLIOGRÁFICAS .......................................................... 79
INTRODUÇÃO
3
1. INTRODUÇÃO
Neste trabalho o escopo está concentrado na análise da volatilidade dos preços da
energia elétrica no Ambiente de Contratação Livre (ACL), mercado à vista, ou seja, spot,
tendo como base uma série temporal univariada do Preço de Liquidação das Diferenças
(PLD) semanal comercializados na Câmara de Comercialização de Energia Elétrica
(CCEE). Sendo esta série utilizada em modelos GARCH3 no objetivo de que capturem e
representem a volatilidade e possibilitem gerar previsões complementares a esta série.
1.1. JUSTIFICATIVA
A justificativa deste trabalho consiste no aumento da eficiência do mercado de
energia elétrica brasileiro, especificamente no ACL a curto prazo, considerando a alta
volatilidade do PLD aqui apresentada e os altos riscos inerentes a tal volatilidade, urge
buscar uma forma de previsão utilizando o modelo GARCH, ferramenta adequada para
capturar ainda que indiretamente a volatilidade inerente e representa-la em previsões úteis
para mitigação destes riscos, no escopo de criar um ambiente de comercialização que vise
estimular os negócios sem onerá-los, razões que motivam o desenvolvimento desta
dissertação.
1.2. DESCRIÇÃO DO PROBLEMA
O problema enfocado neste estudo é a previsão da volatilidade associada aos preços
do PLD para os agentes compradores de energia elétrica no Ambiente de Comercialização
Livre, especificamente no mercado à vista ou spot.
1.3. OBJETIVO PRINCIPAL
O objetivo principal deste trabalho é determinar através de comparações entre os
modelos GARCH, o mais consistente e representativo para a previsão da volatilidade
3
Modelo Auto-Regressivo Generalizado de Heterocedasticidade Condicional (Generalized Auto-Regressive
Conditional Heteroscedasticity).
INTRODUÇÃO
4
associada ao PLD em regime de curto prazo. Efetua-se então uma análise de desempenho
dos modelos de previsão selecionando aqueles que capturem as peculiaridades intrínsecas
dos preços da energia elétrica, através da elaboração de ferramentas computacionais para
simulações baseados no Modelo Auto-Regressivo de Heterocedasticidade Condicional
Generalizado. Tais simulações visam extrair os parâmetros de calibração, simular o
comportamento dos preços no mercado de energia elétrica, efetuar comparações entre os
modelos, identificar o modelo GARCH mais consistente e representativo para a utilização
de previsões do PLD em regime de curto prazo.
1.4. OBJETIVOS ESPECÍFICOS
Para alcançar o objetivo principal do trabalho devem-se atingir alguns objetivos
específicos.

Definir o modelo a ser utilizado com base nas características da série temporal
do PLD considerada.

Verificar a estacionariedade da série temporal (ST) do PLD.

Efetuar transformações necessárias na ST.

Aplicar o modelo ARIMA4 na série de retornos.


•
Medir e quantificar a correlação dos dados da ST.
•
Estimar os parâmetros do Modelo ajustado.
•
Efetuar a escolha do modelo ARIMA mais adequado.
Aplicar o modelo GARCH na série de retornos
•
Medir e quantificar as correlações dos dados da ST.
•
Estimar os parâmetros do Modelo ajustado.
•
Efetuar a escolha do modelo GARCH mais adequado.
Obter a previsão da volatilidade dos retornos com base nos parâmetros
estimados.

Avaliar a coerência dos resultados obtidos, comparando os valores utilizados e
os valores encontrados pelo modelo GARCH.

Sugestões para utilização de outros possíveis modelos de simulação.

Efetuar a validação dos dados, através da análise da estimação dos erros de
previsão.
4
Auto-Regressive Integrated Moving Average.
INTRODUÇÃO
5
1.5. RESULTADOS ESPERADOS
Espera-se neste trabalho, que se possa delinear os mais significativos desempenhos
entre os modelos GARCH, no objetivo de melhor representar a volatilidade associada ao
PLD da commodity5 energia elétrica. Na expectativa de que este trabalho venha
proporcionar subsídios que visem auxiliar estudos similares em outros setores que
necessitem de previsões que comportem uma série temporal semelhante à série utilizada
neste estudo, ou seja, com a volatilidade característica existente nestes dados da série.
Almeja-se também:

Analisar as séries de retornos no objetivo de averiguar a possibilidade de
aplicação dos modelos GARCH.

Calcular e avaliar os parâmetros, analisar as correlações; testar hipóteses e por
fim efetuar previsões com os modelos propostos.

Analisar e adequar os resultados obtidos, considerando e efetuando a
comparação entre os modelos.
1.6. DELIMITAÇÕES DO TRABALHO
Nesta dissertação as delimitações classificadas são:

A série temporal é univariada e possui características de não-linearidade.

Os dados estão dispostos em periodicidade semanal.

Os dados abrangem o período entre 30/06/2001 e 28/02/2013.

O período base para as previsões estão entre 01/01/2005 a 31/12//2010.

As previsões futuras estão dispostas entre 01/01/2011 a 31/12//2012.

Os dados refletem uma série financeira em R$/MWh6.

O modelo GARCH é adequado para utilização em séries financeiras
(MORRETIN E TOLOI, 2006).

No emprego dos modelos GARCH foram utilizadas ferramentas inerentes aos
softwares R7 e EViews8.
5
Produto ou mercadoria de base, bruto, matéria-prima ou grau mínimo de industrialização.
Reais / Mega Watts hora.
7
The R Foundation for Statistical Computing, R Versão x64 2.15.2 (2012-10-26).
8
EViews Version 7.2 Standard Edition – Aug 30 2012 build.
6
INTRODUÇÃO
6
1.7. ORGANIZAÇÃO DO TEXTO
Esta dissertação está organizada em 9 (nove) capítulos e encontra-se com uma
distribuição de acordo com a seguinte estrutura:

No Capítulo 2, expõe-se o Setor Elétrico Brasileiro (SEB) através de um breve
histórico, descrevem-se os ambientes de comercialização, bem como as
principais características da commodity Energia Elétrica.

No Capítulo 3, realiza-se a revisão bibliográfica onde é feito um levantamento
dos principais trabalhos e artigos a respeito dos algoritmos analisados e
utilizados nesta dissertação.

No Capítulo 4, apresenta-se a fundamentação teórica, com os conceitos
principais, tais como métodos de previsão, séries temporais, análise de
regressão, erros de previsão, autocorrelação e a definição de alguns modelos
estatísticos de previsão, como AR, MA, ARMA, ARIMA, SARIMA e modelos
não lineares como GARCH.

No Capitulo 5 descreve-se a metodologia para as simulações no R e EViews.

No Capítulo 6, apresentam-se os resultados obtidos da comparação entre os
algoritmos de previsão, os devidos métodos de testes e validações, bem como
análises preliminares.

No Capítulo 7, expõem-se as conclusões da dissertação.

No Capítulo 8, dispõe-se a divulgação da pesquisa, com a relação, local e
íntegra dos artigos publicados.

E finalizando as sugestões e propostas para trabalhos futuros são apresentadas
no Capítulo 9.
O SETOR ELÉTRICO BRASILEIRO
7
2. O SETOR ELÉTRICO BRASILEIRO
Aborda-se neste capítulo um breve histórico do Setor Elétrico Brasileiro (SEB), a
nova estrutura de comercialização envolvendo o Ambiente de Contratação Livre (ACL) e o
Ambiente de Contratação Regulado (ACR), a singularidade e volatilidade da commodity
energia elétrica, bem como a sua precificação e risco, considerando-se os impactos nos
agentes envolvidos, expondo-se também formas de mitigação destes riscos neste ambiente.
2.1. BREVE HISTÓRICO
Após a crise de abastecimento de energia elétrica ocorrida em 2001 que resultou na
necessidade de racionamento, o impacto social e político foi significativo, logo governo e
sociedade colocaram-se em ação numa nova forma de regulamentação do Setor Elétrico
Brasileiro (SEB). Tal regulamentação ou por assim dizer liberalização dos preços no
escopo de responderem à oferta e demanda, foi efetivada inicialmente através da Lei 9.648,
de 27 de maio de 1998, com a criação do Mercado Atacadista de Energia Elétrica (MAE),
reeditada pela Lei 10.433, de 24 de abril de 2002, substituída pela Lei 10.848 de 15 de
março de 2004, que instituiu a Câmara de Comercialização de Energia Elétrica (CCEE), e
complementada pelo Decreto 5.163 de 30 de julho de 2004, que regulamenta a
comercialização de energia elétrica no mercado brasileiro, com ambientes de
comercialização regulados e livres (MAYO, 2009).
2.2. ACR E ACL
Com a instituição da Câmara de Comercialização de Energia Elétrica (CCEE) as
relações comerciais do atual modelo do Setor Elétrico Brasileiro (SEB) passaram a ocorrer
em dois ambientes distintos: o Ambiente de Contratação Regulada (ACR) e o Ambiente de
Contratação Livre (ACL), sendo que as diferenças entre os montantes gerados, contratados
e efetivamente consumidos são negociados no Mercado de Curto Prazo ou spot (MAYO,
2009; CCEE, 2012).
O SETOR ELÉTRICO BRASILEIRO
8
2.2.1. ACR
No Ambiente de Contratação Regulada (ACR) participam os Geradores, Produtores
Independentes, Comercializadores e os Distribuidores de Energia que representam os
consumidores ditos “cativos”, pois são atendidos exclusivamente pelo distribuidor local,
com tarifas e condições de fornecimento regulados pela Agência Nacional de Energia
Elétrica (ANEEL), através de contratos resultantes de leilões. Estes contratos possuem
regulação específica para aspectos como preço da energia, submercado de registro do
contrato e vigência de suprimento, não sendo passíveis de alterações bilaterais pelos
agentes (MAYO, 2009; CCEE, 2012).
2.2.2. ACL
No Ambiente de Contratação Livre (ACL) a contratação é livremente negociada
através de contratos bilaterais entre os agentes participantes, nestes contratos são
estabelecidos volumes, preços e prazos de suprimento. Observa-se que esses contratos
devem ser obrigatoriamente registrados na CCEE, instituição responsável por realizar a
liquidação financeira das diferenças entre os montantes contratados e os montantes
efetivamente consumidos (CCEE, 2012).
Entre estes agentes estão os Consumidores Livres, cuja demanda mínima deve ser
de 3MW, com tensão igual ou maior que 69kV ou 0,5MW adquirida de uma Pequena
Central Hidroelétrica (PCH) ou fontes alternativas de energias. Os demais agentes são os
Geradores,
Autoprodutores,
Produtores
Independentes,
Consumidores
Especiais,
Comercializadores, Importadores e Exportadores (MAYO, 2009; CCEE, 2012).
No Mercado de Curto Prazo todos os contratos de compra e venda de energia
celebrados seja no ACR ou no ACL devem ser registrados na CCEE, sendo então realizada
a medição dos montantes efetivamente produzidos e/ou consumidos por cada agente. Neste
contexto as diferenças apuradas, sejam de ordem positivas ou negativas, são devidamente
contabilizadas para posterior liquidação financeira neste mercado e valoradas ao Preço de
Liquidação das Diferenças ou comumente denominado PLD.
Desta forma, o Mercado de Curto Prazo pode ser definido como o segmento da
CCEE onde são contabilizadas as diferenças entre os montantes de energia elétrica
contratados pelos agentes e os montantes de geração e de consumo efetivamente
verificados e atribuídos aos respectivos agentes.
O SETOR ELÉTRICO BRASILEIRO
9
Nesta conjuntura de mercado o Ambiente de Contratação Livre (ACL) passou a ser
exposto a um elevado risco de preço, face a alta volatilidade verificada na commodity
energia elétrica no mercado spot, ou seja, Mercado de Curto Prazo ou ainda à vista
(TOLMASQUIM, 2011; CCEE, 2012).
2.3. SINGULARIDADE E VOLATILIDADE
A Energia Elétrica é uma commodity que possui características singulares em
relação às demais commodities9, as quais são:

Não é possível armazena-la ou estoca-la no atacado para futuro uso;

Incerteza da demanda;

Preço inelástico;

Dependente da hidrologia;

Transmissão condicionada ou congestionada;

Oferta e demanda devem ser instantaneamente balanceadas;

Custo da geração tende a forte progressividade face a alta demanda;

Expansão da geração exige longo prazo.
Tais características contribuem para eventuais picos súbitos do preço no mercado
spot de energia elétrica, resultando numa altíssima volatilidade do preço desta commodity
sem similar comparativo no mercado de commodities.
A seguir gráficos da commodity energia elétrica na Figura 1 apresentando elevados
e repetidos picos de curta duração no período de 30/06/2001 a 06/07/2013, que por
comparação com os gráficos das commodities açúcar, ouro e gás natural da Figura 2,
verifica-se claramente a alta volatilidade citada (TOLMASQUIM, 2009; MAYO, 2009;
CCEE, 2013).
9
Plural de commodity.
O SETOR ELÉTRICO BRASILEIRO
10
Figura 1 – Variações de Preços da Commodity Energia Elétrica (CP)
Figura 2 – Gráficos de Variações de Preços de Commodities
Fonte: Mayo, 2009 Apud (AIE/ USA10)
Esta volatilidade pode ser verificada nas demais regiões do país, conforme Figura 3
e nos respectivos retornos11 da série da região SE/CO expostos na Figura 4 em sequência.
Figura 3 – Evolução do PLD Patamar Pesado por Região (CP)
10
11
AIE – Energy Information Administration / United State of America.
Variação relativa dos preços, retorno líquido simples ou taxa de retorno. Vide página 35 Equação (10).
O SETOR ELÉTRICO BRASILEIRO
11
Figura 4 – Retorno Simples do PLD Região SE/CO Patamar Pesado (CP)
A seguir na Figura 5 gráficos de evolução do PLD por região, expondo as
diferenças, a exemplo do ano de 2005 estável na região SE/CO, mas volátil na região SUL.
Reais / MWh
NE_P
NORTE_P
600
600
500
500
400
400
300
300
200
200
100
100
0
0
2005
2006
2007
2008
2009
2010
2005
2006
SECO_P
2007
2008
2009
2010
2009
2010
SUL_P
600
600
500
500
400
400
300
300
200
200
100
100
0
0
2005
2006
2007
2008
2009
2010
2005
2006
2007
2008
2005 a 2010 - Período Semanal
Figura 5 – Gráficos de Evolução do PLD por Região – Patamar Pesado (CP)
O SETOR ELÉTRICO BRASILEIRO
12
Na Figura 6 sobrepõem-se o preço e o log-retorno12 do PLD.
Figura 6 – Sobreposição do Preço e Log-Retorno do PLD de Energia Elétrica (CP)
2.4. A PRECIFICAÇÃO E RISCO
A precificação normal de uma commodity está relacionada a diversos fatores, mas
basicamente a oferta e a demanda, bem como a seus níveis de estoques e peculiaridades
envolvidas a estes últimos, porém como visto anteriormente a commodity energia elétrica
não pode ser armazenada. Possui ainda demanda incerta e também fortes componentes de
sazonalidade, sendo o preço a vista sensível a variações climáticas. Tais componentes
tornam a energia elétrica uma commodity de elevado risco (LYRA, 2005).
2.5. IMPACTOS NOS AGENTES
Dentre as novas regras do SEB foi criado um órgão que visa viabilizar as
negociações entre os agentes da commodity energia elétrica no mercado brasileiro,
denominado Câmara de Comercialização de Energia Elétrica (CCEE).
Os agentes da CCEE são as empresas que atuam no setor de energia elétrica nas
áreas
de
geração,
distribuição,
comercialização:
importadores,
exportadores
comercializadores, além dos consumidores livres e consumidores especiais.
12
Retorno composto continuamente ou simplesmente log-retorno.
e
O SETOR ELÉTRICO BRASILEIRO
13
Na Figura 7 a seguir expõe-se a estrutura de comercialização vigente no mercado
de energia elétrica brasileiro (RODRIGUES, 2007).
Figura 7 – Estrutura de Comercialização do SEB.
Fonte: Rodrigues, 2007
A seguir a descrição das atuações de cada agente no SEB:
2.5.1. Geração
Os Agentes de Geração podem vender a energia produzida através de contratos
celebrados no ACR ou no ACL.
Os Geradores de Serviço Público e os Produtores Independentes de Energia devem
apresentar lastro, proveniente de geração própria e contratos de compra, para atendimento
a 100% do montante de seus contratos de venda.
Existem os Autoprodutores, os quais geram energia para seu uso exclusivo e
podem, mediante autorização da ANEEL, vender o excedente de geração por meio de
contratos (CCEE, 2012).
Nestes casos a verificação do lastro é realizada mensalmente, com base nos dados
de geração e contratos de venda dos últimos 12 meses. A não comprovação de lastro
sujeita o agente ao pagamento de penalidades.
No âmbito dos geradores que são os fornecedores de energia elétrica o preço spot
visa a cobrir a posição de oferta, observando-se níveis de reservatório, hidrologia,
sazonalidade, bem como aspectos climáticos e custos de operação (CCEE, 2012).
O SETOR ELÉTRICO BRASILEIRO
14
2.5.2. Distribuição
Os Agentes de Distribuição, ditos concessionárias, devem adquirir energia para
suprimento de seu mercado consumidor, por meio de contratos celebrados no Ambiente de
Contratação Regulada, advindos de leilões de energia. Nesse caso, devem apresentar
cobertura, proveniente de contratos de compra, para atendimento de 100% de seu consumo
verificado de energia.
Esta verificação da cobertura contratual é realizada na contabilização do mês de
janeiro de cada ano, com base nos dados de consumo e contratos de compra do ano
anterior. A não comprovação de cobertura do consumo sujeita o agente ao pagamento de
penalidades (CCEE, 2012).
Conforme regras estabelecidas no Decreto 5.163/2004, os distribuidores estão
sujeitos a penalidades, quando a energia contratada diverge da demanda requisitada pelos
seus consumidores, causando a sobre ou a subcontratação, no entanto observa-se que existe
o Mecanismo de Compensação de Sobras e Déficits (MCSD) que permite que as
concessionárias compensem entre si montantes de energia elétrica adquiridos em leilões de
empreendimentos existentes, promovendo o repasse de energia entre agentes de
distribuição com sobras ou déficits declarados no objetivo de minimizar estes riscos
(BURATTI, 2008).
Sobrecontratação
No caso de sobrecontratação, é admitido que 3% do total da energia contratada em
excesso, sejam repassados às tarifas dos consumidores finais, sem qualquer penalização
para os distribuidores. No entanto para valores acima do limite de 3%, haverá o risco
financeiro do mercado de curto prazo, uma vez que a diferença entre o total de energia
contratada e o mercado demandado pelos consumidores, verificado mensalmente na
CCEE, é vendido ao Preço de Liquidação das Diferenças (PLD), no mercado spot. Assim,
caso o PLD seja superior ao preço médio contratado, a concessionária aufere lucro, e em
situação inversa, assume o prejuízo (BURATTI, 2008).
Subcontratação
Na ocorrência de subcontratação, a energia faltante para atender a demanda dos
consumidores é automaticamente comprada no mercado spot, pelo preço da PLD.
Conforme o Artigo 42 do Decreto 5.163, o repasse do custo desta compra se dará pelo
O SETOR ELÉTRICO BRASILEIRO
15
menor valor entre o preço PLD e o Valor de Referência13 (VR), calculado pela ANEEL.
Nesta situação, os distribuidores contabilizarão o prejuízo financeiro se o preço PLD pago
pela energia for superior ao valor de referência VR, que será utilizado para repassar o custo
para as tarifas. De outra forma, se o PLD estiver com seu preço menor ou igual ao valor de
referência VR, não haverá prejuízo, pois o repasse será efetuado pelo mesmo valor pago
pela energia. Não obstante o resultado financeiro da subcontratação for nulo, no melhor
dos casos, ou negativo na pior situação, haverá a aplicação de uma penalidade adicional,
calculada sobre cada MWh não contratado (BURATTI, 2008).
Para as distribuidoras ou concessionárias que compram a energia a ser consumida
pelos clientes ditos “cativos”, a subcontratação representa alto risco de penalidade e de
compra no mercado spot, pois estará à mercê do preço daquele momento, no qual poderá
encontrar situações hidrológicas, climáticas e mercadológicas adversas (MAYO, 2009;
CCEE, 2012).
2.5.3. Comercialização
Agentes Comercializadores de Energia
Os Agentes Comercializadores podem comprar e vender energia por meio de
contratos celebrados no ACL ou ACR, no caso específico do ACR contratos de venda aos
Agentes de Distribuição.
Os agentes comercializadores podem representar na CCEE usinas pertencentes a
produtores independentes e autoprodutores que não tenham participação obrigatória na
CCEE, conforme definições da Convenção de Comercialização.
Para isto devem apresentar lastro, proveniente de geração própria ou contratos de
compra, para atendimento a 100% do montante de seus contratos de venda de energia.
A verificação do lastro é realizada mensalmente, com base nos dados de geração e
contratos de compra e de venda dos últimos 12 meses. A não comprovação de lastro sujeita
o agente ao pagamento de penalidades
Para estes agentes o ganho entre as diferenças de compra e venda lhe são salutares
quando o mercado encontra-se em relativo equilíbrio, ou seja, não há uma forte e
duradoura escassez na oferta ou na demanda (CCEE, 2012).
13
Valor utilizado para regular o repasse às tarifas dos consumidores finais dos custos de aquisição de energia
elétrica (CCEE, 2012).
O SETOR ELÉTRICO BRASILEIRO
16
2.5.4. Consumidores Livres
Os Consumidores Livres devem apresentar cobertura, proveniente de contratos de
compra, para atendimento de 100% de seu consumo verificado de energia.
Essa verificação é realizada mensalmente, com base nos dados de consumo
verificado e contratos de compra dos últimos 12 meses. A não comprovação de cobertura
do consumo sujeita o agente ao pagamento de penalidades.
Assim como os distribuidores, os consumidores livres também possuem riscos de
subcontratação, situação em que estarão expostos às nuances do mercado spot (CCEE,
2012).
2.5.5. Importadores e Exportadores
Os Agentes de Importação podem vender a energia produzida através de contratos
celebrados no ACR ou no ACL, devendo apresentar lastro, proveniente de geração própria
ou contratos de compra, para atendimento a 100% do montante de seus contratos de venda.
Essa verificação do lastro é realizada mensalmente, com base nos dados de geração
e contratos de compra e de venda dos últimos 12 meses. A não comprovação de lastro
sujeita o agente ao pagamento de penalidades.
Excluem-se da necessidade de comprovação de lastro os casos em que a importação
de energia tenha características emergencial, temporária e interruptível.
Os contratos de exportação de energia estão isentos da necessidade de comprovação
de lastro para venda de energia (MAYO, 2009; CCEE, 2012).
2.6. MITIGAÇÃO DE RISCOS NO AMBIENTE DE ENERGIA ELÉTRICA
As atividades econômicas sempre acarretam riscos, negócios com energia elétrica
estão inclusos, neles o sucesso econômico depende fortemente do preço de mercado da
energia elétrica.
Os principais riscos com os quais os agentes participantes do mercado de energia
elétrica
deparam-se,
embora
interdependentes (MAYO, 2009).
classificados
separadamente,
são
na
realidade
O SETOR ELÉTRICO BRASILEIRO
17
Dentre os mais importantes pode-se elencar:

Risco de preço de mercado definido como a ameaça de perdas causadas pela
alta volatilidade dos preços de energia elétrica.

Risco de preço de combustível que é específico de usinas termelétricas,
extrapola o mercado de energia elétrica, mas afeta a capacidade de o gerador
suprir este mercado.

Risco da contraparte relativas às ameaças de perdas causadas pela
inadimplência, seja no pagamento, seja na entrega da energia pela contraparte
(MAYO, 2009).
Para minimizar inicialmente tais riscos em função da preponderância de usinas
hidrelétricas no parque de geração brasileiro, são utilizados modelos matemáticos14 para o
cálculo do PLD, que têm por objetivo encontrar a solução ótima de equilíbrio entre o
benefício presente do uso da água e o benefício futuro de seu armazenamento, medido em
termos da economia esperada dos combustíveis das usinas termelétricas (CCEE, 2012).
Em um sistema hidrotérmico como o brasileiro, com substancial parcela de geração
hidroelétrica, o volume de água nos reservatórios ao longo do período de planejamento é
desconhecido, pois depende de chuvas que ainda irão ocorrer. Esta característica gera
incertezas às decisões de despacho presentes e consequências sobre a operação do sistema
e formação de preços no futuro. O fluxograma da Figura 8 a seguir ilustra este fato:
Figura 8 – Fluxograma de Operação de um Sistema Hidrotérmico.
Fonte: D´ARAÚJO, 2009
14
Programação Dinâmica Recursiva.
O SETOR ELÉTRICO BRASILEIRO
18
Outras características de um sistema hidrotérmico são:

Imperfeita previsão de afluências futuras no instante inicial torna o problema
essencialmente estocástico;

Grande quantidade de reservatórios e a necessidade de otimização multiperíodo
torna o problema de grande porte;

Não linearidade devido à função de produção de energia das hidroelétricas;

Custos indiretos relacionados com os benefícios de geração hidroelétrica;

Necessidade de considerar o uso múltiplo da água: navegação, controle de
cheias, irrigação, saneamento e abastecimento de água.
O operador do sistema deve comparar o beneficio imediato do uso da água com o
beneficio futuro de seu armazenamento. Este problema é tratado e ilustrado a seguir
(MAYO, 2009).
A Função de Custo Imediato (FCI) mede os custos de geração térmica e déficit
(corte de carga) no estágio t. Note que o custo imediato aumenta à medida que diminui a
utilização de recursos hidráulicos, ou seja, à medida que aumenta o volume de água
armazenado no final do período. A Função de Custo Futuro (FCF) está associada ao custo
esperado de geração térmica e déficit do final do estágio t (início de t+1) até o final do
período do planejamento da operação (MAYO, 2009).
Figura 9 – Funções de Custos
Esta função diminui à medida que aumenta o volume armazenado final, pois haverá
mais energia hidráulica no futuro, portanto, pode-se dizer que a derivada do custo futuro
em relação ao volume armazenado dos reservatórios é o valor da água. A FCF é calculada
por meio de simulações probabilísticas da operação do sistema para cada nível de
armazenamento ao final do estágio t, considerando diversos cenários hidrológicos. O ponto
O SETOR ELÉTRICO BRASILEIRO
19
que minimiza o custo de operação imediato e futuro corresponde ao ponto onde as
derivadas das funções de custo imediato e custo futuro se igualam em módulo.
2.6.1. Preço de Liquidação das Diferenças – PLD
As relações comerciais entre agentes são regidas predominantemente por contratos
de compra e venda de energia, os quais, sem exceção, devem ser registrados no CCEE.
Esse registro vincula a contratação de longo e médio prazo ao mercado de curto prazo, pois
toda e qualquer transação de energia não registrada mediante contratos está sujeita à
contabilização e à liquidação, de forma compulsória, no mercado de curto prazo da CCEE
(TOLMASQUIM, 2011).
No processo de contabilização, as diferenças entre os volumes contratados e os
efetivamente movimentados são contabilizadas pela CCEE e liquidadas no mercado de
curto prazo. Isso permite que as partes “zerem” suas posições por meio de compra ou
venda de energia elétrica, em base mensal, pelo preço de mercado de curto prazo, ou Preço
de Liquidação das Diferenças (TOLMASQUIM, 2011).
O PLD é utilizado para valorar a energia comercializada no mercado de curto prazo
ou spot e se faz pela utilização dos dados considerados pelo Operador Nacional do Sistema
(ONS) para a otimização da operação do Sistema Interligado Nacional (SIN), refletindo o
Custo Marginal de Operação (CMO), usado como aproximação do preço de equilíbrio do
mercado, diferenciando-se dele por ter um valor máximo ou teto, e um valor mínimo ou
piso regulatórios15. Expressado a seguir na Figura 10 (MAYO, 2009).
Figura 10 – Curva de Oferta e Demanda e Custo Marginal de Operação
Fonte: (D´ARAÚJO, 2009)
15
A partir de 1 de janeiro de 2013 a ANEEL autorizou variar entre R$14,13 e R$780,03/MWh.
O SETOR ELÉTRICO BRASILEIRO
20
Neste processo de valoração a Agência Nacional de Energia Elétrica (ANEEL)
possui a atribuição de autorizar o uso de modelos computacionais utilizados no
planejamento e na operação tanto pelo SIN quanto pelo ONS no cálculo do PLD que é
determinado semanalmente para cada patamar de carga e para cada submercado, e
utilizado na CCEE. Dentre estes modelos fazem parte o programa denominado NEWAVE,
um modelo estratégico de geração hidrotérmica que visa resolver os problemas de
planejamento da operação interligada de sistemas hidrotérmicos empregando a técnica de
programação dinâmica dual estocástica. E o DECOMP, programa de planejamento de
despacho em curto prazo, cujo objetivo é determinar as metas de geração de cada usina de
um sistema hidrotérmico sujeito a afluências estocásticas, de forma a atender a demanda e
minimizar o valor esperado do custo de operação ao longo do período de planejamento
para isto utiliza a técnica de programação linear, representando as características físicas e
as restrições operativas das usinas hidroelétricas de forma individualizada (MAYO, 2009;
CCEE, 2012).
2.6.2. Formas de Mitigação de Riscos
Nesta conjuntura de mercado o ACL passou a ser exposto a um elevado risco de
preço, face a alta volatilidade verificada na commodity energia elétrica. No objetivo de
minimizar tais riscos tornou-se necessário desenvolver mercados de derivativos16 de
energia elétrica com o intuito de oferecer aos agentes ferramentas para o gerenciamento
dos riscos de preço (MAYO, 2009).
2.6.3. Mecanismo de Realocação de Energia – MRE
Face às dimensões territoriais do Brasil, existem fatores climáticos, hidrológicos e
estruturais entre as diversas regiões que acabam por tornar crucial que as gerações das
usinas hidrelétricas e térmicas estejam sujeitas ao despacho centralizado regido pelo ONS,
observando-se as disponibilidades das usinas que estão em condições de geração. Tais
despachos ocorrem de modo a se obter minimização dos custos operativos e o menor custo
marginal, face às afluências hidrológicas e armazenamento de água dos reservatórios,
considerando-se também, os preços ofertados pelas usinas térmicas e as restrições
operativas destas (MAYO, 2009; CCEE 2012).
16
Instrumento financeiro cujo preço deriva do preço de um bem ou de outro instrumento financeiro.
O SETOR ELÉTRICO BRASILEIRO
21
Neste contexto os Agentes Geradores sujeitos ao despacho centralizado, não
possuem controle sobre seu nível de geração. Todavia, períodos secos e úmidos não
coincidentes, fazem com que existam transferências de energia entre regiões, ou seja, uma
região em período seco deve armazenar água, produzindo abaixo da média, enquanto que
uma região úmida produz acima da média. Não obstante isto, outro fator importante na
concepção do MRE é a existência de várias usinas em cascata, em que o ótimo individual
não necessariamente corresponde ao ótimo conjunto. Sendo o despacho centralizado em
que a água pertence a todos, logo o seu uso não é decidido pelo proprietário da usina, e sim
pelo ONS, sendo então o MRE o instrumento que minimiza e compartilha entre os agentes
de geração o risco de venda de energia em longo prazo. Assim o MRE realoca a energia,
transferindo o excedente daqueles que geraram além de suas Garantias Físicas17 para
aqueles que geraram abaixo (MAYO, 2009; CCEE, 2012).
2.6.4. Mecanismo de Compensação de Sobras e Déficits – MCSD
Este mecanismo tem o escopo de permitir que os agentes de distribuição, ou seja, as
concessionárias, compensem entre si montantes de energia elétrica adquiridos em leilões
de empreendimentos existentes, promovendo o repasse de energia entre agentes de
distribuição com sobras ou déficits declarados, sendo os agentes cedentes e agentes
cessionários, respectivamente. Estas declarações são voluntárias e este mecanismo aplicase exclusivamente aos Contratos de Compra de Energia no Ambiente Regulado
(CCEARs), no Ambiente de Contratação Regulado, conforme previsto no Decreto nº
5.163/04 (CCEE, 2012).
2.6.5. Derivativos de Energia Elétrica
Os derivativos são instrumentos financeiros cuja formação dos preços está sujeita à
variação de preços de outros ativos, mais precisamente dos seus respectivos ativos-objetos,
ou seja, está associada à ideia de que os preços desses contratos possuem uma estreita
ligação, derivando do preço de ativo subjacente ao contrato. Sua utilização visa reduzir ou
neutralizar o risco de variação na precificação de determinado ativo; ou como
investimento, buscando lucro pela assunção do risco.
17
Corresponde à fração a ela alocada da Garantia Física do Sistema, sendo à máxima carga que pode ser
suprida a um risco prefixado de 5% de não atendimento da mesma.
O SETOR ELÉTRICO BRASILEIRO
22
Existem três espécies principais de derivativos: os swaps, as operações em
mercados a termos e futuros e as opções. Negociados em bolsas de energia ou em
mercados de balcão, esses contratos desempenham papel primário de oferecer formação
transparente de preços futuros e certeza de preço aos geradores, distribuidores e
consumidores livres (MAYO, 2009; CCEE, 2012).
Contratos a Termo
Acordo de compra e venda de energia elétrica para entrega futura a um preço
prefixado estipulado em contrato. Tendo em vista sua flexibilidade e liquidez os contratos
a termo são mais utilizados como instrumentos de gerenciamento de risco no mercado de
energia elétrica.
Contratos Futuros
Semelhantes aos contratos a termo, os contratos futuros, diferem por sua alta
padronização nas especificações tipo: locais de entrega, requisitos transacionais e
requisitos de liquidação sendo em sua maioria liquidados financeiramente com ajustes
diários.
Swap de Energia Elétrica
São contratos financeiros que permitem aos seus titulares pagar um preço fixo pela
energia elétrica ativo-objeto, indiferentemente da flutuação de seu preço, ou vice-versa,
durante o período contratual. Utilizados para garantir a certeza de preço no curto e médio
prazos.
Opções
Diferem dos contratos futuros e swap por oferecer o direito, porém sem a obrigação
de celebrar um contrato a um preço, volume e prazo no futuro acordados, mediante
pagamento ao vendedor de um prêmio por essa flexibilidade adicional. Existem diversos
tipos de opções, mas baseiam-se em dois principais, a Européia que somente poderá ser
exercida em sua data de vencimento e a Americana que poderá ser exercida a qualquer
tempo até a sua data de vencimento (MAYO, 2009).
REVISÃO BIBLIOGRÁFICA
23
3. REVISÃO BIBLIOGRÁFICA
Neste capitulo expõe-se uma breve revisão bibliográfica com os principais modelos
de análise e previsão de séries temporais e os respectivos autores.
Séries Temporais – ST
Segundo Gujarati (2006) uma ST é um conjunto de observações dos valores que
uma variável assume em diferentes momentos do tempo, podendo esses dados serem
coletados a intervalos regulares, que podem ser de forma diária, semanal, mensal,
trimestral, semestral, anual ou ainda em intervalos extremamente curtos de forma quase
contínua a exemplo das cotações das ações.
Modelos de Previsão
Modelos de previsão estatística são baseados na utilização dos dados históricos a
partir de uma série temporal, tais modelos visam capturar características intrínsecas da
série e criar estimativas que possibilitem gerar previsões.
Movimento Browniano Geométrico – MGB
O MGB em homenagem ao botânico e físico escocês Robert Brown que efetuou a
primeira observação em 1827 quando verificou que pequenas partículas contidas nos
vacúolos dos grãos de pólen executavam pequenos movimentos aparentemente aleatórios.
Conhecido também como Processo de Wiener, em honra a Norbert Wiener um matemático
norte-americano que o formalizou matematicamente em 1923, sendo um processo
estocástico contínuo, utilizado para modelagem de evolução de preços. O MGB foi
destacado como promissor por descrever movimentos aleatórios e obter valores
estritamente maiores que zero, com distribuição normal e variância constante, sendo uma
vantagem face aos preços serem estritamente positivos. Porém apesar de uma ampla
aceitação no mercado financeiro como alternativa, a utilização no mercado de energia
elétrica é desaconselhada em dois pontos principais: a dificuldade em capturar e
representar a complexa estrutura da volatilidade, e a impossibilidade deste processo gerar
picos de preços com a magnitude dos observados na commodity em estudo (MAYO, 2009).
REVISÃO BIBLIOGRÁFICA
24
3.1. MODELO ARMA – (1960)
Os primeiros trabalhos datam de 1927 com os modelos auto-regressivos estudados
por George Udny Yule, posteriormente Gilbert Thomas Walker e suas contribuições para
as Equações de Yule-Walker e o algoritmo de Durbin Watson para regressões.
Sendo o modelo ARMA a junção do modelo AR(p) ou Auto-Regressivos com
ordem
e o modelo MA(q)18 ou médias móveis com ordem
, que proporcionam a
vantagem de um número menor de parâmetros, que superam a individualidade destes
modelos. Convém ressaltar que não são adequados para modelarem relações não-lineares,
no entanto são importantes para a compreensão de séries temporais estacionárias e os
modelos de análises, ou seja, a base dos modelos auto-regressivos (MORETTIN E TOLOI,
2006; GUJARATI, 2006).
3.2. MÉTODO DE BOX-JENKINS – (1970)
No decorrer da década de 1960 os professores George E. P. Box e Gwilym M.
Jenkins desenvolveram artigos sobre a teoria de controle e análise de séries temporais.
Esses artigos culminaram com a publicação em 1970 do livro “Time Series Analysis,
Forecasting and Control”, o qual apresentava uma metodologia para a análise de séries
temporais, sendo a versão de 1976 a mais referenciada. Segundo Gujarati (2006), nesta
metodologia Box e Jenkins reuniram técnicas existentes não para construir modelos com
equações únicas ou simultâneas, mas na análise das propriedades probabilísticas ou
estocásticas das séries econômicas segundo a filosofia de “Deixar que os dados falem por
si”. Neste sentido a metodologia de Box-Jenkins será extremamente importante no
desenvolvimento deste trabalho no que tange a identificação da ST em relação aos modelos
AR(p), MA(q), ARMA(p,q) ou ARIMA(p,d,q)19 (GUJARATI, 2006).
3.3. MODELO ARIMA – (1976)
Nos modelos ARMA(p,q) e anteriores, a média e a variância das séries
estacionárias são constantes, e as covariâncias não variam com o tempo, entretanto muitas
18
19
Moving Average.
Auto-Regressive Integrated Moving Average.
REVISÃO BIBLIOGRÁFICA
25
séries temporais econômicas são não-estacionárias, ou seja, integradas. Neste sentido se for
efetuada uma ou mais diferenciações
que torne a série estacionária possibilitando a
aplicação do modelo ARMA(p,q), diz-se que a série temporal é auto-regressiva integrada
de médias móveis, ou ARIMA(p,d,q). Este conceito incluso pelos estatísticos George Box
e Gwilym Jenkins em 1976, torna o modelo conhecido também por Modelo de BoxJenkins (GUJARATI, 2006; MORETTIN E TOLOI, 2006).
3.4. MODELO – SARIMA – (1976)
Quando uma série temporal apresenta comportamento periódico dentro de um
intervalo de tempo de até 12 meses, denomina-se sazonalidade, podendo este intervalo ser
anual, semestral, mensal, semanal e etc. Então torna-se necessário acrescentar uma
componente sazonal no modelo. O modelo sazonal multiplicativo proposto por Box e
Jenkins em 1976, utiliza-se da componente sazonal incorporada ao modelo ARIMA(p,d,q),
denominado SARIMA, sendo os componentes sazonais auto-regressivos SAR(P) e a média
móvel SMA(Q), representado como SARIMA (p,d,q) (P,D,Q), onde D é a ordem de
diferenciação sazonal. Salienta-se que neste trabalho este modelo não será utilizado, face a
inadequação frente as características da série temporal em estudo (MORETTIN E TOLOI,
2006).
3.5. MODELO DE ENGLE – ARCH – (1982)
Dada às restrições do modelo ARIMA em manter a variância do erro constante ao
longo do tempo, Engle em 1982, propôs um modelo alternativo para previsões,
denominado ARCH (Auto-Regressive Conditional Heterocedasticity) no objetivo de
estimar a variância da inflação, o qual lhe rendeu o Prêmio Nobel de Economia em 2003.
Modelo este que introduz a variância condicional do erro determinada pela
defasagem do erro ao quadrado. O modelo ARCH (q), em que q é o número de defasagens
do erro ao quadrado, pode ser representado como (ENGLE, 1982; GUJARATI, 2006):
=
(1)
+
;
REVISÃO BIBLIOGRÁFICA
26
Em que é a variância condicionada e
e são parâmetros a serem estimados.
3.6. MODELO DE BOLLERSLEV – GARCH – (1986)
No entanto, dada o grande número de defasagens q frequentemente encontrados no
modelo ARCH, Bollerslev em 1986 sugeriu um modelo geral e simplificado denominado
GARCH (Generalized Auto-Regressive Conditional Heteroscedasticity). Este modelo
apresenta uma vantagem operacional ao incorporar a própria variância condicional passada
como fator determinante da variância condicional do erro. Dessa forma, o modelo GARCH
(p,q), onde p é o número de defasagens do erro ao quadrado e q o número de defasagens da
própria variância condicional ao quadrado, sendo representado por:
=
+
;
Em que
,
e
(2)
+
;
são parâmetros a serem estimados (BOLLERSLEV, 1986;
MORETTIN E TOLOI, 2006).
FUNDAMENTAÇÃO TEÓRICA
27
4. FUNDAMENTAÇÃO TEÓRICA
Morettin e Toloi (2006) afirmam que em Economia existem dois procedimentos
predominantes:
Econométrico:
O analista baseia-se firmemente na teoria econômica objetivando construir um
modelo, incluindo nele muitas variáveis que representam o fenômeno em análise.
Estatístico:
O estatístico ou de séries temporais, deixa que “os dados falem por si” no escopo de
construir um modelo ou estar preparado para utilizar um, ainda que não se
harmonize com a teoria econômica, que possa porém, produzir melhores previsões.
Nesta dissertação apresenta-se um estudo das características e comportamento de
uma série temporal univariada dos preços da eletricidade no mercado de energia elétrica
brasileiro, especificamente o PLD no ACL a curto prazo ou mercado spot, no objetivo de
efetuar melhores previsões e desta forma mitigar os riscos associados a este mercado.
Neste objetivo torna-se necessário a compreensão de modelos que possam capturar e
melhor explicitar características intrínsecas a esta série, representando-a e possibilitando a
composição de previsões mais aproximadas da realidade. Neste sentido este capítulo visa
abordar alguns conceitos fundamentais de séries temporais, métodos de previsão, análise
de regressão, erros de previsão, autocorrelação bem como definições dos modelos lineares
de previsão, como AR, MA, ARMA, ARIMA, SARIMA e modelos não lineares como
ARCH e GARCH (LYRA, 2005; MORETTIN E TOLOI, 2006; GUJARATI, 2006).
4.1. SÉRIES TEMPORAIS
Segundo expõe Morettin e Toloi (2006) uma série temporal é qualquer conjunto de
observações ordenadas cronologicamente, ou seja, valores que possuem ordenação no
tempo.
FUNDAMENTAÇÃO TEÓRICA
28
Tais séries podem ser de ordem univariadas ou multivariadas, contínua ou discreta:
 Univariadas
Baseados em apenas uma série histórica.
Exemplo: Histórico de preços da energia elétrica semanal (PLD). Modelo
utilizado nesta dissertação.
 Multivariadas
Baseados em mais de uma série histórica.
Exemplo: Registro da temperatura e pressão de um ponto no oceano.
 Contínua
Quando o conjunto de observações geradas sequencialmente ao longo do tempo
for definido em um intervalo contínuo.
Exemplo: Registro de maré no porto de Santos.
 Discreta
Quando o conjunto de observações é registrado em tempos específicos,
geralmente em intervalos equidistantes.
Exemplo: Valores diários de poluição no estado de São Paulo.
Morettin e Toloi (2006) também observam que uma série temporal discreta pode
ser obtida através da amostragem de uma série temporal contínua em intervalos de tempos
iguais.
4.1.1. Tipos de Modelos
Na análise de séries temporais existem basicamente dois enfoques, convém
ressaltar que em ambos, o escopo é construir modelos para as séries com propósitos
determinados, denominados modelos paramétrico e não-paramétrico: (MORETTIN E
TOLOI, 2006):
 Modelos Paramétricos
A análise ocorre no domínio temporal, ou seja, com um número finito de
parâmetros.
Exemplo: Modelo AR20, ARMA21 e ARIMA22.
20
Auto-Regressivo ou Auto-Regressive.
Auto-Regressivo de Médias Móveis ou Moving Average.
22
Auto-Regressivo Integrado de Médias Móveis ou Auto-Rlegressive Integrated Moving Average.
21
FUNDAMENTAÇÃO TEÓRICA
29
 Modelos Não-Paramétricos
A análise ocorre no domínio da frequência, podem ter um número infinito de
parâmetros.
Exemplo: Modelos de Redes Neurais e Análise Espectral.
Observa-se que estes modelos devem ser simples e parcimoniosos, conforme
relatam Morettin e Toloi (2006), no sentido de que o número de parâmetros envolvidos
tenda ao mínimo possível.
No entendimento de Morettin e Toloi (2006) modelos para descrever séries
temporais são processos estocásticos, ou seja, processos controlados por leis
probabilísticas. Sendo a definição de processo estocástico dada por:
Seja
( ),
∈
=
um conjunto arbitrário. Um processo estocástico é uma família
, tal que, para cada ∈ ,
( )
é uma variável aleatória ou doravante (v.a.).
Nestas condições, um processo estocástico é uma família de variáveis aleatórias, as
quais supomos definidas num mesmo espaço de probabilidades (Ω, Α, Ρ). O conjunto
= {0, ±1, ±2, ±3 … } ou o
normalmente tomado como o conjunto dos números inteiros
conjunto dos números reais ℝ. Outrossim, para cada
na realidade
( )
∈ ,
é
( )
será uma v.a. real. Assim,
definida por Ω é uma função de dois argumentos, ( , ),
∈ ,
∈ Ω.
Esta interpretação de processo estocástico pode ser verificada na Figura 11 a seguir
(MORETTIN E TOLOI, 2006).
Figura 11 – Processo estocástico visto como uma família de variáveis aleatórias.
Fonte: Morettin e Toloi, 2006.
Observa-se na Figura 11, que para cada
∈ , existe uma v.a. ( , ), com uma
distribuição de probabilidades; sendo possível que a Função Densidade de Probabilidade
(FDP) no instante t seja diferente da FDP no instante t , para dois instantes
e
quaisquer, porém a situação usual é aquela em que a FDP de ( , ) é a mesma para todo
FUNDAMENTAÇÃO TEÓRICA
∈ .Não obstante, para cada
30
∈ Ω fixado, obtém-se uma função de , ou seja, uma
realização ou trajetória do processo, ou ainda, uma Série Temporal. Pode-se considerar
também esta distribuição de probabilidades uma família de trajetórias, vista na Figura 12.
Figura 12 – Um processo estocástico interpretado como uma família de trajetórias.
Fonte: Morettin e Toloi, 2006.
4.1.2. Componentes Básicas
Morettin e Toloi (2006) observam que os objetivos principais da análise de uma
série temporal são:

Investigar o mecanismo gerador da série temporal.

Criar previsões de valores futuros da série de curto ou longo prazo.

Descrever graficamente o comportamento da série verificando a existência de
tendências, ciclos e variações sazonais, construção de histogramas e diagramas
de dispersão e etc.

Verificar periodicidades relevantes através de análise espectral.

Modelagem do fenômeno sobre consideração.

Obtenção de conclusões em termos estatísticos.

Avaliação da adequação do modelo em termos de previsão.
Desta forma a aplicação de análise de séries temporais baseia-se na utilização de
dados históricos no escopo de obter modelos de previsão. Sendo objeto fundamental
determinar as componentes básicas para identificar um padrão de comportamento da série
que permita uma melhor compreensão que possibilite gerar previsões (GUJARATI, 2006).
FUNDAMENTAÇÃO TEÓRICA
31
Tais padrões podem conter tendências, ciclos, sazonalidades, variações irregulares e
variações randômicas (CARDOSO, 2005: Apud MAKRIDAKIS et al., 1983).
 Tendência
Indica o comportamento de longo prazo de uma série, ou seja, se ela sobe desce
ou permanece estável, observando também se a tendência é constante, linear ou
quadrática.
Figura 13 – Tipos de Tendências de uma Série Temporal
Fonte: Barros, 2012.
 Ciclos
Indicam padrões que se repetem na série em períodos superiores a um ano.
Exemplo: Ciclos relacionados às atividades econômicas ou meteorológicas.
Figura 14 – Padrão Cíclico em torno de 10 ou 11 anos
Fonte: Ehlers, 2007.
 Sazonalidade
Indica a repetição de um padrão na série dentro do período de um ano.
Exemplo: Vendas de sorvetes, altas no verão e baixas no inverno.
Figura 15 – Tendência e Sazonalidade
Fonte: Ehlers, 2007.
FUNDAMENTAÇÃO TEÓRICA
32
 Variações irregulares
São alterações advindas de fatores excepcionais, os quais não podem ser
previstos e, logo, inclusos no modelo.
Exemplo: Catástrofes climáticas.
Figura 16 – Variação Irregular em 1915
Fonte: Ehlers, 2007.
 Variações randômicas (Aleatoriedade ou Erro Residual)
Caracterizadas por sua duração curta e intensidade variável, esta componente é
denominada “ruído”. Por apresentar estas variações não podem ser modeladas
pelas técnicas gerais de previsão e são, de modo geral, tratadas pelas médias e
desvios padrão ou variâncias. (CARDOSO, 2005: Apud MENTZER E
BIENSTOCK, 1998)
Morettin e Toloi (2006) relatam ainda que uma série temporal pode ser descrita
como uma função conforme a Equação (3) a seguir:
= ( )+
,
Em que ( ) denomina-se sinal e
= 1, 2, 3 … , ,
(3)
nomeia-se como ruído.
Considerando esta forma, tem-se várias classes de modelos, destacando-se os
modelos de erro ou regressão, modelos estruturais e modelos não-lineares (MORETTIN E
TOLOI, 2006).
Não obstante estes padrões uma ST pode ser classificada também quanto ao
comportamento da variância, que pode apresentar-se de formas diferentes em relação às
dispersões, seja com homocedasticidade23 ou heterocedasticidade24, fator de suma
importância para a escolha de modelos que a representem (GUJARATI, 2006).
23
24
Homo (igual) e Cedasticidade (dispersão).
Hetero (desigual) e Cedasticidade (dispersão).
FUNDAMENTAÇÃO TEÓRICA
33
Homocedasticidade
No entendimento de Gujarati (2006), a variância de
variância condicional de
para cada
é um número positivo constante igual a
, ou seja, a
. Representando a
premissa de igual dispersão ou homocedasticidade e utilizando-se o gráfico da Figura 17,
significa que as populações Υ correspondentes aos valores de Χ têm a mesma variância
,
ou ainda que a variação em torno da linha de regressão ou linha das relações médias entre
Χ e Υ é a mesma para todos os Χ, não aumenta nem diminui quando Χ varia.
Figura 17 – Homocedasticidade
Fonte: Gujarati, 2006.
Este conceito está expresso na Equação (4) a seguir.
( | )= [
− ( | )] = (
)=
(4)
Heterocedasticidade
Conforme expõe Morettin e Toloi (2006) contrariamente ao exposto no item
anterior, a variância condicional da população Υ varia com Χ, numa dispersão desigual,
denominada adequadamente como heterocedasticidade, visto na Figura 18.
Conceito que está expresso na Equação (5) a seguir, nela observa-se o subscrito
em
indicando que a variância da população Υ não é mais constante.
( | )=
A seguir a Figura 18 expondo a dispersão desigual ou heterocedasticidade.
(5)
FUNDAMENTAÇÃO TEÓRICA
34
Figura 18 – Heterocedasticidade
Fonte: Gujarati, 2006.
Estacionariedade
Quando a série temporal se desenvolve no tempo aleatoriamente ao redor de uma
média μ constante, refletindo alguma forma de equilíbrio estável (GUJARATI, 2006).
4.1.3. Transformações
Morettin e Toloi (2006) indicam que existem duas motivações básicas para efetuar
transformações nos dados originais de uma série temporal: estabilizar a variância e tornar o
efeito sazonal aditivo. As transformações podem ser do tipo logarítmica, por diferenças,
através de retornos e etc. Neste trabalho se utilizará apenas as diferenças e os retornos, pois
são os adequados a série temporal utilizada.
Diferenças
Gujarati (2006) cita que na maioria dos procedimentos de análise estatística de
séries temporais supõe-se que estas sejam estacionárias. Em caso negativo será então
necessário transformar os dados originais, sendo que a transformação mais comum consiste
em tomar diferenças sucessivas da série original, até que se obtenha uma série estacionária.
Neste procedimento será suficiente tomar uma ou duas diferenças para o êxito. Observa-se
que tomar mais diferenças que o necessário tende a degenerar a série causando assim
perdas significativas de informações. Define-se na Equação (6) a primeira diferença de Z :
FUNDAMENTAÇÃO TEÓRICA
35
ΔZ = Z − Z
(6)
Sendo de modo geral a n-ésima diferença de Z definida por:
Δ Z = Δ[Δ
Z]
(7)
Retornos
Um dos objetivos da análise de séries temporais financeiras é a avaliação de riscos
do ativo que a série representa, sendo o risco medido em termos de variações de preços
deste ativo, este preço ou
num determinado período que neste trabalho refere-se a uma
semana, poderá ter uma variação entre os instantes
− 1 e , ou seja, Δ
=
−
,
sendo a variação relativa ou retorno líquido simples, entre os mesmos instantes expresso na
Equação (8) (MORETTIN E TOLOI, 2006):
R =
P −P
P
=
ΔP
P
(8)
O retorno composto continuamente ou log-retorno sendo expresso conforme
Equação (9) a seguir.
r = log
P
ΔP
= (1 + R )
P
P
(9)
Nos modelos não-lineares será utilizada a Equação (10) exposta a seguir, doravante
denominada apenas de retornos:
X = ln(P ) − ln(P
)
(10)
No entendimento de Gujarati (2006) retornos financeiros aqui expostos apresentam
características peculiares que muitas séries temporais não apresentam, tais como:

Raramente apresentam tendência ou sazonalidade25;

São em geral não-autocorrelacionados;

Os quadrados dos retornos são autocorrelacionados, apresentando uma
correlação de defasagem pequena e depois uma queda lenta das demais;
25
Eventual exceção de retornos intra-diários.
FUNDAMENTAÇÃO TEÓRICA

36
Séries de retornos apresentam agrupamentos de volatilidades ou “Clusters” ao
longo do tempo.

A distribuição (incondicional) dos retornos apresenta caudas mais pesadas do
que uma distribuição normal;

A distribuição embora aproximadamente simétrica é em geral leptocúrtica26;
Na análise da série temporal do PLD com o modelo GARCH serão utilizados os
retornos da ST face às características expostas (MORETTIN E TOLOI, 2006).
4.1.4. Dados Discrepantes ou Outliers
No estudo da estatística, o termo outliers ou discrepante, ou ainda valor atípico,
refere-se a uma observação que apresenta um grande afastamento das demais da ST,
podendo implicar em prejuízos a interpretação dos resultados dos testes estatísticos
aplicados às amostras. No entendimento de Gujarati (2006) o estudo de Outliers, que
independe das causas, pode ser efetuado em três fases distintas:
1. Identificação
Fase inicial que aponta geralmente, por análise gráfica ou em caso de pequeno
número de dados, por observação direta dos mesmos, as observações
potencialmente aberrantes e possivelmente Outliers.
2. Verificação
Na segunda fase as observações identificadas como potenciais Outliers são
testadas através da aplicação de um critério estatístico para verificar a
inconsistência com os demais valores.
3. Decisão de Eliminação
Na terceira e última fase torna-se necessário decidir como proceder com as
observações discordantes ou Outliers. Uma solução simples consiste em
eliminar tais observações. Todavia tais observações consideradas como Outliers
devem ser tratadas cuidadosamente, pois contêm informações relevantes sobre
características subjacentes aos dados e poderão ser decisivas no conhecimento
da população pertencente a amostra em estudo (MORETTIN E TOLOI, 2006;
GUJARATI, 2006).
26
A Curtose k, em que k representa grau de elevação (Leptocúrtica: k>3) ou achatamento (Platicúrtica: k<3).
FUNDAMENTAÇÃO TEÓRICA
37
Neste trabalho face a escassa quantidade de observações (313), optou-se por um
expurgo de valores que permitisse manter a série temporal do PLD próximo da média dos
picos máximos, conforme Tabela 1 a seguir.
Tabela 1 – Substituição de Valores Considerados Outliers
SUBSTITUIÇAO DOS OUTLIERS
DADOS
Originais
Expurgos Substituídos
475,53
200,00
275,53
11/01/2008
569,59
260,00
309,59
18/01/2008
569,59
260,00
309,59
25/01/2008
550,28
250,00
300,28
01/02/2008
4.2. MODELOS DE PREVISÃO
A commodity energia elétrica constitui o maior desafio para os pesquisadores e os
agentes de mercado no âmbito de modelar o comportamento do seu preço, sendo que os
processos de simulação do preço formam a base dos sistemas de apreçamento dos
derivativos e de gerenciamento de risco. O processo escolhido deve compor ferramentas
que capturem as principais características dos preços da energia elétrica para que tenha
confiabilidade, mas também deve ser de baixa complexidade, evitando assim uma
sobrecarga computacional, impedindo desta forma a utilização nas plataformas de
comercialização (MAYO, 2009).
Existem duas abordagens distintas para modelar os preços da energia elétrica:
Abordagem fundamental ou econométrica
Baseada num modelo que utiliza a simulação da operação do sistema e do mercado
para chegar aos preços de mercado, utilizando-se o Custo Marginal de Geração (CMG) e o
consumo esperado. No Setor Elétrico Brasileiro (SEB) a Agência Nacional de Energia
Elétrica (ANEEL) utiliza-se de diversos modelos interconectados de forma a proporcionar
ao Operador Nacional do Sistema (ONS) uma operação otimizada do Sistema Integrado
Nacional (SIN), dentre estes modelos destacam-se o NEWAVE e o DECOMP
(GUJARATI, 2006; MAYO, 2009; CCEE, 2012).
FUNDAMENTAÇÃO TEÓRICA
38
Abordagem estatística
Segundo Gujarati (2006), baseia-se na tradição financeira de modelar diretamente o
comportamento estocástico dos preços de mercado a partir de dados históricos e da análise
estatística.
A primeira abordagem é mais realística, porém torna-se proibitiva face ao alto custo
computacional visto o grande número de cenários a serem considerados, não sendo
utilizada neste trabalho. A segunda abordagem oferece baixo custo com adequação para
capturar as características peculiares dos preços da energia elétrica, motivo pelo qual será
utilizada (MAYO, 2009; GUJARATI, 2006).
Então, utilizando a abordagem estatística, e de conformidade com entendimento de
Morettin e Toloi (2006) de que a maioria dos métodos de previsão baseia-se na ideia de
que observações passadas contêm informações sobre o padrão de comportamento da série
temporal. O propósito dos métodos é distinguir o padrão de qualquer ruído27 que possa
estar contido nas observações e então usar esse padrão para prever valores futuros da série.
Este ruído  representa uma sequência de choques aleatórios e independentes uns com os
outros, ε é uma porção não controlável do modelo é chamado normalmente de ruído
branco, considerado como tendo distribuição normal, média zero, variância constante e
não-correlacionados (MORETTIN E TOLOI, 2006).
Convém ressaltar que a hipótese de erros não-correlacionados causa limitações para
validar e descrever o comportamento de séries econômicas como a deste estudo, onde os
erros observados são autocorrelacionados e influenciam a evolução do processo, todavia
como exposto anteriormente existem diversos tipos de modelos de previsão, entre eles os
paramétricos, não-paramétricos, lineares e não-lineares, os quais são expostos a seguir
(GUJARATI, 2006):
4.2.1. Modelos Lineares
Conforme entendimento de Gujarati (2006) modelos estatísticos podem ser lineares
nas variáveis ou nos parâmetros, no entanto em termos de modelos de regressão aqui
apresentados referem-se a regressão linear nos parâmetros.
27
Intitulado também como Ruído Branco (White noise).
FUNDAMENTAÇÃO TEÓRICA
4.2.1.1.
39
Modelos de Erro ou Regressão
Neste modelo ( ) esta determinada como uma função do tempo, com componente
uma sequência aleatória, que independe de ( ).
sistemática ou determinística, sendo
Supõe-se ainda que nestas condições as variáveis aleatórias
sejam não-correlacionadas,
tenham média zero e variância constante, ou seja, desta forma qualquer efeito do tempo
influencia somente a parte determinística ( ) (MORETTIN E TOLOI, 2006).
Morettin e Toloi (2006) referem-se ainda a variantes deste modelo como:
Modelo de Tendência Linear
Em que ( ) = α + βt, é uma função linear dos parâmetros, dado que:
Z( ) = α + βt + α( ) , t = 1, 2, 3, … , N.
(11)
Modelo de Regressão
Em que ( ) = α + β , continua a ser uma função linear dos parâmetros e
uma
quantidade fixa observável, em que:
Z( ) = α + β
+ α( ) , t = 1, 2, 3, … , N.
(12)
Movimento Geométrico Browniano – MGB
Representado pelo modelo de precificação de Black-Scholes28, sendo um processo
estocástico contínuo que obtém valores estritamente maiores que zero, dado que os preços
são estritamente positivos. Apesar de ampla aceitação é desaconselhável no mercado de
energia elétrica, pois dificulta a captura da estrutura complexa de volatilidade dos ativos
energéticos, tais como: volatilidade estrutural, sazonalidade, flutuações e tendências. Não
sendo possível também gerar picos de preços com a magnitude dos observados no mercado
de energia elétrica (MAYO, 2009).
28
O conceito fundamental de Black-Scholes é que uma opção é implicitamente precificada se a ação é
negociada. O valor de uma opção varia apenas com o preço da ação e com o tempo até o vencimento.
FUNDAMENTAÇÃO TEÓRICA
4.2.1.2.
40
Modelos de Suavização Exponencial – MSE
Morettin e Toloi (2006) expõe que uma grande classe de métodos de previsão que
tenta tratar ambas as causas de flutuações em séries de tempo é a das suavizações. Técnicas
especificas desse tipo assumem que os valores extremos da série representam a
aleatoriedade e, assim, por meio da suavização desses extremos, pode-se identificar o
padrão básico. Estes métodos possuem grande popularidade devido à simplicidade, à
eficiência computacional e à sua razoável precisão. Nesta classe destacam-se:
Suavização Exponencial Simples – SES
Sendo uma média ponderada, este processo atribui pesos maiores as observações
mais recentes mas, quanto menor for o valor de “” mais estáveis serão as previsões finais,
visto que a utilização de valores menores de “” implica que pesos maiores serão
atribuídos as observações passadas e, consequentemente, quaisquer flutuações aleatórias,
no presente, exercerá um peso menor no cálculo da previsão.
Representado pela Equação (13) abaixo:
̅ =
(1 − )
+ (1 − )
, = 1, … , ,
Onde ̅ denomina-se valor exponencialmente suavizado e
de suavização com valores de: 0 ≤
(13)
representa a constante
≤ 1.
Vantagens: Fácil entendimento, aplicação não dispendiosa, grande flexibilidade
permitida pela variação da constante de suavização “”, necessidade de armazenar
somente
,
e . Para valor de  =
este fornece previsões semelhantes ao método de
médias móveis que será abordado em seguida.
Desvantagens: Dificuldade em determinar o valor mais apropriado da constante de
suavização “” (MORETTIN E TOLOI, 2006).
4.2.1.3.
Modelo de Médias Móveis – MA (Moving Average)
Conhecido também como Médias Móveis Simples (MMS), consiste em calcular a
média aritmética das r observações mais recentes, com r = 2, 3, 4 ..., O nome média móvel
é utilizado porque, a cada período, a observação mais antiga é substituída pela mais
FUNDAMENTAÇÃO TEÓRICA
41
recente, calculando-se uma média nova, sendo a previsão de todos os valores futuros dado
pela última média móvel calculada.
Vantagens: Simples aplicação, aplicável com um número pequeno de observações
e permite uma flexibilidade grande devido à variação de r de acordo com o padrão da série.
Desvantagens: Deve ser utilizado apenas para prever séries estacionárias, caso
contrário a precisão das previsões será muito pequena, pois os pesos atribuídos às r
observações são todos iguais e nenhum peso é dado às observações anteriores a esse
período (MORETTIN E TOLOI, 2006).
4.2.1.4.
Modelo Auto-Regressivo – AR
Gujarati (2006) afirma que o termo regressão foi criado por Francis Galton, num
famoso artigo em que Galton verificou que, embora houvesse uma tendência que os pais
altos tivessem filhos altos e os pais baixos, filhos baixos, a estatura média das crianças
nascidas de pais com dada altura tendiam a mover-se ou “regredir” para a altura média da
população como um todo, conforme Figura 19 a seguir.
Figura 19 – Distribuição hipotética das alturas dos filhos em relação às alturas dos pais
Fonte: Gujarati, 2006
Gujarati (2006) ainda observa que apesar de Galton estar interessado no motivo de
haver estabilidade na distribuição de alturas em uma população, o objetivo moderno
concentra-se em como a altura média dos filhos varia, dada a altura dos pais, ou seja, nosso
escopo é prever a altura média dos filhos a partir do conhecimento da altura de seus pais.
Neste sentido a análise de regressão ocupa-se do estudo da dependência de uma variável, a
variável dependente, em relação a uma ou mais variáveis, as variáveis explanatórias, no
FUNDAMENTAÇÃO TEÓRICA
42
objetivo de estimar e/ou prever o valor médio da população da variável dependente em
termos de valores conhecidos ou fixados das explanatórias (GUJARATI, 2006).
Sendo a definição de um modelo Auto-Regressivo (AR) exposta na Equação (14).
=Φ
Em que
+Φ
+ ⋯+Φ
+
(14)
corresponde à observação da série temporal no tempo t;
Φ Corresponde ao parâmetro do modelo AR de ordem p e
representa o erro de
eventos aleatórios que não podem ser explicados pelo modelo. No caso em que as
observações da série temporal possam ser representadas pela Equação (14), e a ordem do
modelo puder ser determinada e os parâmetros estimados, então será possível prever o
valor futuro da série em análise (GUJARATI, 2006).
Conforme expressado anteriormente ressalta-se que este modelo não é adequado
para modelar relações não-lineares, caso deste trabalho, entretanto é importante para a
compreensão de séries temporais estacionárias e os modelos de análises, ou seja, a base dos
modelos auto-regressivos (MORETTIN E TOLOI, 2006l; GUJARATI, 2006).
4.2.1.5.
Modelo Auto-Regressivo de Médias Móveis – ARMA
Sendo o modelo ARMA um processo misto do modelo AR(p) ou auto-regressivos
com ordem
e o modelo MA(q) ou médias móveis com ordem , que proporcionam
vantagens, como menor quantidade de parâmetros, que superam a individualidade destes
modelos. O modelo ARMA(p,q) pode ser escrito na forma da Equação (15) a seguir:
=Φ
+⋯+ Φ
+
−θ
− ⋯−θ
(15)
Convém ressaltar que não são adequados para modelarem relações não-lineares, no
entanto são importantes para a compreensão de séries temporais estacionárias e os modelos
de análises, ou seja, a base dos modelos auto-regressivos (MORETTIN E TOLOI, 2006).
4.2.1.6.
Modelo AR Integrado de Média Móvel – ARIMA
O modelo ARIMA (Auto-Regressive Integrated Moving Average), introduzido por
Box e Jenkins em 1976 baseia-se pela estimação da regressão da variável dependente
função das defasagens da própria variável , indicado por
função dos erros aleatórios, indicado por
em
termos auto-regressivos, e em
termos de média móvel. Como a maioria das
FUNDAMENTAÇÃO TEÓRICA
43
séries temporais econômicas são naturalmente não-estacionárias, a aplicação do modelo
ARIMA ( , , ) exige a transformação das mesmas, por
estacionárias, ao passo que a ordem
e
diferenças, para torná-las
pode ser obtida pela função de autocorrelação ou
ACF29 e a função de autocorrelação parcial ou PACF30, sendo auxiliadas pela ordem que
minimiza o critério de Akaike ou AIC31, que é uma medida da relação de qualidade do
ajuste de um modelo estatístico ou ainda o critério de Schwarz. O modelo pode ser
apresentado como na Equação (16) seguinte:
∆y = Φ +
β∆
;
+ε +
αε
(16)
;
Em que ∆é o operador de diferenças, ε o termo de erro e Φ, βe αparâmetros a
serem estimados. Observa-se que para verificação de estacionariedade aplica-se o teste de
raiz unitária (MORETTIN E TOLOI, 2006; GUJARATI, 2006).
4.2.2. Modelos Não-Lineares
Segundo Morettin e Toloi (2006) os modelos lineares não são adequados para
descrever o comportamento de séries temporais que apresentam variância condicional
evoluindo no tempo ou simplesmente volatilidade. Todavia os modelos não-lineares, assim
considerados pois são não-lineares na variância, a exemplo do ARCH, GARCH e suas
variantes, além de modelos de volatilidade estocástica, são modelos mais apropriados para
capturar e representar a volatilidade, que é a variância condicional de uma variável,
comumente um retorno. Convém esclarecer que a volatilidade seja medida indiretamente,
manifesta-se de várias formas numa série temporal, são elas (PEÑA ET AL, 2001, Cap 9,
apud MORETTIN E TOLOI, 2006):

A volatilidade aparece em grupos ou aglomerações de maior ou menor
variabilidade, denominados ¨Clusters¨;

A volatilidade evolui continuamente no tempo, podendo ser considerada
estacionária;

A volatilidade reage de modo diferente a valores positivos ou negativos da
série.
29
Autocorrelation Function.
Partial Autocorrelation Function.
31
Akaike Information Criterion.
30
FUNDAMENTAÇÃO TEÓRICA
44
Pode-se dizer de modo geral que uma série temporal econômica ou financeira é
não-linear quando responde de forma diferente a choques grandes ou pequenos.
Sendo o objetivo deste trabalho utilizar o modelo GARCH para capturar e
representar a volatilidade de modo a efetuar previsões do PLD, o foco estará diretamente
neste modelo (MORETTIN E TOLOI, 2006; GUJARATI, 2006).
4.2.3. Modelos ARCH e GARCH
Pesquisadores
observaram
em
séries
temporais
financeiras,
que
existe
autocorrelação na variância σ no período t, quando os seus valores estão defasados em um
ou mais períodos, de forma similar com que o termo de erro μ no período t está
correlacionado com o termo de erro no período t − 1 em um esquema AR(1) ou com
vários termos de erro em um esquema geral AR(p).
Destaca-se que a autocorrelação não se restringe a relações entre termos de erros
atuais e passados, mas também a variâncias do erro atuais e passadas.
Esta autocorrelação verificada quando a variância do erro se relaciona ao quadrado
dos termos de erro do período anterior denomina-se Heterocedasticidade Condicional
Auto-Regressiva. A identificação ocorre utilizando-se o Modelo Auto-Regressivo
Condicional Heterocedástico ou ARCH32.
No entanto, quando a variância do erro se relaciona ao quadrado dos termos do erro
em vários períodos do passado denomina-se Heterocedasticidade Condicional AutoRegressiva Generalizada. Sendo identificada utilizando-se o Modelo Generalizado AutoRegressivo Condicional Heterocedástico ou GARCH33, os quais expõe-se a seguir
(GUJARATI, 2006).
4.2.3.1.
Modelo AR de Heterocedasticidade Condicional – ARCH
Em 1982 Robert Fry Engle III propôs a modelagem de um processo com objetivo
de estimar a variância da inflação, o qual lhe rendeu o Prêmio Nobel de Economia em
2003. Baseando-se no fato de que o retorno X é não-correlacionado serialmente, mas a
variância condicional, ou seja, a volatilidade depende de retornos passados através de uma
função quadrática (MORETTIN E TOLOI, 2006; ENGLE, 1982).
32
33
Auto-Regressive Conditional Heteroscedasticity.
General Auto-Regressive Conditional Heteroscedasticity.
FUNDAMENTAÇÃO TEÓRICA
45
Este modelo com forma auto-regressiva com heterocedasticidade condicional
denomina-se ARCH, sendo que um modelo ARCH(q) pode ser representado por:
X =
h =α +α X
hε
(17)
+⋯+α X
(18)
Em que ε é uma sequencia de variáveis aleatórias independentes e identicamente
distribuídas (i.i.d), com média zero e variância igual a um, α > 0, α ≥ 0, i > 0,
usualmente ε ~ (0,1) ou ε ~t quando representa uma distribuição
de Student com
graus de liberdade (MORETTIN E TOLOI, 2006; ENGLE, 1982).
Alguns fatos sobre o modelo:

Coeficientes α devem satisfazer determinadas condições, dependentes das
imposições sobre X .

Valores grandes de X precedem outros valores grandes.

Retornos costumam apresentar caudas longas com curtose > 3.

Quanto mais restrições forem impostas ao processo X , mais restrições terão os
coeficientes do modelo.

Face a X pertencer a parte do cálculo na fórmula da volatilidade, retornos
positivos e negativos são tratados de forma similar e;

Retornos grandes e isolados podem conduzir a super-previsões.
Em resumo o modelo ARCH( ) introduz a variância condicional do erro
determinada pela defasagem do erro ao quadrado, em que
é o número de defasagens dos
erros ao quadrado, porém, devido ao grande número de defasagens
frequentemente
encontrados no modelo ARCH um modelo complementar foi proposto (MORETTIN E
TOLOI, 2006; ENGLE, 1982).
4.2.3.2.
Modelo Generalizado ARCH – GARCH
Uma generalização natural dos modelos ARCH foi proposta por Bollerslev em
1986, e ficou conhecida como GARCH. Como em muitas aplicações é requerido que o
modelo ARCH apresente muitos lags ( ) ou defasagens, os modelos GARCH estendem a
formulação ARCH no sentido de que permita uma memória mais longa, e uma estrutura de
FUNDAMENTAÇÃO TEÓRICA
46
defasagens para a variância mais flexível e parcimoniosa, deste modo pode descrever a
volatilidade com menos parâmetros. Sendo estes modelos utilizados no melhor
entendimento da relação entre a volatilidade e os retornos esperados. O modelo
GARCH( , ) pode então ser representado por:
X =
(19)
hε
(20)
h =α +
αX
+
βh
Em que ε é uma sequência de variáveis aleatórias independentes e identicamente
distribuídas (i.i.d), com média igual a zero e variância igual a um, α > 0, α ≥ 0, β ≥ 0
∑
(α + β ) > 1, q = max( , ), usualmente ε ~ (0,1) ou ε ~t
uma distribuição
de Student com
quando representa
graus de liberdade (MORETTIN E TOLOI, 2006;
ENGLE, 1982; BOLLERSLEV, 1986).
Alguns fatos sobre o modelo:

Vantagens e desvantagens são similares ao modelo ARCH.

Altas volatilidades são precedidas por retornos ou volatilidades grandes.

Difícil identificação da ordem do modelo a série.

Necessidade de utilização de vários critérios para especificação do modelo a ser
ajustado.
Convém ressaltar que os modelos ARCH e GARCH tratam simetricamente os
retornos, pois a volatilidade é uma função quadrática destes, porém a volatilidade
comporta-se de maneira assimétrica aos retornos, com tendência a respostas maiores para
retornos negativos que a positivos (MORETTIN E TOLOI, 2006; ENGLE, 1982;
BOLLERSLEV, 1986).
4.3. CRITÉRIOS DE AVALIAÇÃO E ERROS
Para avaliar a precisão das previsões produzidas pelos diferentes modelos, são
utilizados alguns tipos de critérios de avaliação e magnitude de erros conforme segue:
FUNDAMENTAÇÃO TEÓRICA
47
4.3.1. Critérios de Avaliação – AIC, JB, LB e ADF
4.3.1.1.
Akaike Information Criterion – AIC
Extensamente utilizado, baseia-se na imposição de uma punição pelo acréscimo de
regressores ao modelo, sendo que ao comparar dois ou mais modelos, o preferido será
aquele que apresentar menor valor AIC.
l
k
+2
T
T
AIC = −2
(21)
Onde o termo "l" é o valor do logaritmo da função de probabilidade com os
parâmetros estimados usando "T" observações. Os vários critérios de informação são todos
baseados em -2 vezes a função de verossimilhança média, ajustada por uma função de
penalidade (GUJARATI, 2006; EVIEWS®; R®).
4.3.1.2.
Schwartz Information Criterion – SIC
Semelhante ao AIC com a característica de impor uma penalidade maior pela
inclusão de coeficientes adicionais a serem estimados (GUJARATI, 2006).
SC = −2
Em que
l
log(T)
+k
T
T
e o fator de punição e
4.3.1.3.
e o fator de punição e
4.3.1.4.
o número de observações.
Hannan-Quinn Criterion – HQC
HQC = −2
Em que
(22)
l
log log(T)
+ 2k
T
T
(23)
o número de observações.
Jarque-Bera – JB
O teste de normalidade Jarque-Bera trata-se de um teste assintótico ou de grande
amostra, calculando primeiramente a assimetria e a curtose dos resíduos. Expresso na
Equação (24) a seguir:
JB =
(K − 3)
N
S +
6
4
(24)
FUNDAMENTAÇÃO TEÓRICA
Em que
48
representa o tamanho da amostra,
e
os coeficientes de assimetria e
curtose, respectivamente. Salienta-se que para uma variável normalmente distribuída,
=0e
= 3. Portanto o teste JB de normalidade é um teste de hipótese conjunta de
iguais a 0 e 3, e espera-se que o valor de
e
= 0, sob a hipótese nula de que os resíduos
são normalmente distribuídos. Observa-se que o teste JB deve ser utilizado em grandes
amostras e neste estudo utiliza-se um valor médio com 312 amostras (GUJARATI, 2006;
EVIEWS®; R®).
4.3.1.5.
Ljung-Box – LB
O teste de Ljung-Box (LB) é uma variante de um teste de Box-Pierce ajustado a
amostras pequenas, para valores elevados da ordem de autocorrelação, r. Representando o
coeficiente de correlação entre valores da mesma variável desfasados k períodos por p , a
estatística de Ljung-Box será descrita por:
Q( k) = N ∙ ( N + 2 ) ∙
(25)
1
∙p
N−i
A qual tem uma distribuição X ( ) na hipótese nula (conjunta) dos coeficientes de
correlação (GUJARATI, 2006; EVIEWS®; R®).
4.3.1.6.
Teste Dickey-Fuller Aumentado – ADF
No entendimento de Gujarati (2006), Dickey e Fuller em 1979 demostraram através
de resultados da distribuição assintótica obtida e simulações dos mesmos valores críticos34
para vários testes e tamanhos de amostras que, sob a hipótese nula de raiz unitária, esta
estatística não segue a distribuição t de Student convencional. Considere uma ST
representada por
, onde
é um termo de erro de ruído branco e
o tempo cronológico,
conforme Equação (26) infra:
Y = ρY
34
+u
−1 ≤ ρ ≤ 1
MacKinnon (1991) produziu estimativas que permitem o calculo de valores críticos para rejeição da
hipótese nula para qualquer tamanho de amostra.
(26)
FUNDAMENTAÇÃO TEÓRICA
49
Regredindo, ou seja, subtraindo Y
Y −Y
de ambos os lados, obtém-se a Equação (27),
= ρY
−Y
+u
(27)
Que pode ser escrita como exposto na Equação (28) a seguir.
= ( ρ − 1) Y
Y −Y
+u
(28)
E finalmente se resume a Equação (29) abaixo:
∆Y = δY
+u
(29)
Em que δ = (ρ − 1) e ∆ o Operador de Primeiras Diferenças.
Quando ρ = 1, caso da raiz unitária, Y se torna um modelo de passeio aleatório
sem deslocamento, logo um processo estocástico não-estacionário. Então regredindo Y em
relação ao seu valor defasado Y
, verifica-se se ρ = 1, caso seja, a ST é dita Não-
Estacionária. Testa-se então a hipótese nula de que δ = 0. Sendo δ = 0 ⇒ ρ = 1, tem-se
então uma raiz unitária significando que a ST é Não-Estacionária.
O simples teste de raiz unitária de Dickey-Fuller descrito acima só é válido se a
série é um processo AR simples. Sendo a ST relacionada a atrasos de ordem superior, a
suposição de distúrbios de ruído branco é violada. O Teste de Dickey-Fuller Aumentado
(ADF) constrói uma correção paramétrica para correlação de ordem superior (GUJARATI,
2006).
(30)
∆Y = β + β t + δY
+
α ∆Y
Onde ε é um termo de erro de ruído branco puro e ∆Y
(Y
−Y
+ε
= (Y
−Y
), ∆Y
=
) (...). O número de termos de diferenças defasados a ser incluído é, muitas
vezes, determinado empiricamente, sendo que a ideia é incluir um número de termos
suficientes no escopo de que o termo de erro não apresente correlação serial.
4.3.2. Critérios de Erros: RMSE, MAPE, MAE
No objetivo de comparar as performances dos modelos escolhidos são utilizados
alguns tipos de critérios de erros conforme segue:
FUNDAMENTAÇÃO TEÓRICA
4.3.2.1.
50
Root Mean Square Error – RMSE
(31)
RMSE =
1
M
σ −σ
Em que σ representa o valor previsto, σ o valor real e
4.3.2.2.
Mean Absolute Percentage Error – MAPE
MAPE ∗=
1
M
(32)
σ −σ
Em que σ representa o valor previsto, σ o valor real e
4.3.2.3.
o tamanho da amostra.
o tamanho da amostra.
Mean Absolute Error – MAE
Em estatística o MAE é o erro absoluto médio de previsão, uma medida de quão
próximos estão às previsões do real, representado pela Equação (33) a seguir:
MAE =
Em que
1
N
| −
representa o erro absoluto,
|=
1
N
(33)
| |
o valor previsto,
tamanho da amostra (GUJARATI, 2006; EVIEWS®).
o valor real e
o
METODOLOGIA PARA AS PREVISÕES E SIMULAÇÕES
51
5. METODOLOGIA PARA AS PREVISÕES E SIMULAÇÕES
Gujarati (2006) afirma que a questão fundamental ao debruçar-se sobre uma série
temporal consiste em quando utilizar um processo:

Auto-Regressivo puro AR(p), qual seria o valor de .

Médias móveis MA(q), e assim sendo, qual seria o valor de .

ARMA(p,q), e neste caso, quais seriam os valores de

ARIMA(p,d,q), sendo necessário conhecer os valores de ,
e q.
e .
Nesta situação ele ainda observa que o método de Box-Jenkins descrito a seguir é
extremamente útil para responder a estas indagações.
Método de Box-Jenkins
Morettin e Toloi (2006) ratificam e expõem que a metodologia Box-Jenkins
consiste em ajustar modelos auto-regressivos integrados e de médias móveis,
ARIMA(p,d,q), a um conjunto de dados e posteriormente após estes ajustes aplica-los aos
modelos generalizados auto-regressivos de heterocedasticidade condicional GARCH(p,q),
efetuar novos ajustes a um conjunto de dados e finalmente gerar as previsões. Sendo a
estratégia para construção do modelo calcada num ciclo iterativo, em que a escolha da
estrutura do modelo baseia-se nos próprios dados.
Os quatro estágios do ciclo iterativo são descritos abaixo e na Figura 20 a seguir:
1. Especificação – Onde uma classe de modelos é considerada para análise;
No caso deste estudo especificamente a classe de modelos escolhida foi o
GARCH, devido a capacidade de captura da estrutura da volatilidade e
representação em previsões.
2. Identificação – Nesta fase há a identificação de um ou mais modelos
ARIMA/GARCH com base na análise das funções de autocorrelações (ACF),
autocorrelações parciais (PACF), a função de verossimilhança35 (LLF) e
critérios a exemplo do critério de informação de Akaike (AIC).
3. Estimação – Após a escolha de um ou mais modelos identificados como os mais
adequados efetua-se a estimação dos parâmetros destes modelos.
35
Log-Likelihood Function.
METODOLOGIA PARA AS PREVISÕES E SIMULAÇÕES
52
4. Verificação – Finalmente na verificação efetua-se o diagnóstico da existência de
convergência e erros do modelo ajustado, analisando-se os resíduos para
confirmar a adequação no objetivo de efetuar a previsão.
Figura 20 – Método de Box-Jenkins (CP)
Observa-se que para modelar e ajustar o GARCH(p,q), torna-se necessário
previamente modelar e ajustar o ARIMA(p,d,q)
Não havendo a adequação do modelo o ciclo é repetido retornando a fase de
identificação. Gujarati (2006) ressalta que um procedimento geralmente utilizado baseia-se
em identificar não apenas um único modelo, mas alguns modelos que devem ser estimados
e verificados, escolhendo entre os modelos não apenas um, mas os que possuírem os
menores erros ou critérios AIC.
A fase crítica do procedimento descrito é a identificação, relatam Morettin e Toloi
(2006, p.105), e ainda observam que há a possibilidade de que vários pesquisadores
identifiquem modelos diferentes para a mesma série temporal. Citam ainda que uma
desvantagem da técnica de Box e Jenkins está em que a utilização requer conhecimento e
larga experiência associados ao uso de software específico.
Gujarati (2006, p.678) adverte que ao efetuar esta análise, busca-se uma
semelhança entre as funções teóricas e amostrais das ACF e PACF que apontem a direção
METODOLOGIA PARA AS PREVISÕES E SIMULAÇÕES
53
correta para a elaboração de modelos ARIMA(p, d, q) e GARCH(p,q). Razão pela qual a
modelagem destes exige grande habilidade, necessitando de extensiva prática devido a
significativa complexidade.
A metodologia utilizada baseia-se em quatro pontos principais descritos a seguir:
5.1. IDENTIFICAÇÃO
Identificados os valores de p, d e q, ou seja, os valores das defasagens e do grau de
diferenciação apropriados para a série temporal tornar-se estacionária. Sendo utilizados
correlogramas, baseados na função de autocorrelação (ACF) e autocorrelação parcial
(PACF), os testes estatísticos: Akaike info criterion (AIC) e Schwarz info criterion (SIC), e
o teste de raiz unitária utilizado foi o Argumented Dickey-Fuller (ADF).
5.2. ESTIMAÇÃO
Estimados os parâmetros dos modelos utilizando o método de máxima
verossimilhança para obtenção dos modelos GARCH.
5.3. VERIFICAÇÃO
Avaliar os modelos estimados realizando-se o teste de raiz unitária ou ADF na série
de resíduos dos modelos. O teste mostrou que todos os resíduos foram estacionários e que
os modelos tiveram o máximo ajuste.
5.4. PREVISÃO
Após o ajuste dos modelos verificou-se a potencialidade de previsão. Para isso,
estimaram-se os modelos tendo preservado uma parte da série dos dados para verificação
do desempenho da previsão. Desta forma, pode-se comparar os valores previstos com a
série real.
RESULTADOS OBTIDOS
54
6. RESULTADOS OBTIDOS
Com base na metodologia de Box-Jenkins foram obtidos os dados das simulações
da série temporal do PLD nos softwares Eviews® e R®, utilizando inicialmente os modelos
ARIMA(p,d,q) como base e posteriormente o GARCH(p,q), sendo que ambos após ajustes
possibilitaram a geração das previsões.
6.1. RESULTADOS OBTIDOS NO R®
Conforme Tabela 2 a seguir gerou-se no software R® o sumário estatístico da série
temporal do PLD no período de 01/01/2005 a 31/12/2010 da região SE/CO.
Tabela 2 – Sumário Estatístico da Série Temporal do PLD no R®(CP)
SUMÁRIO ESTATÍSTICO DO R®
Observações Mínimo Mediana Média Máximo
313
12.80
52.97
74.54
569.60
Observa-se na Figura 21 a não estacionariedade da série temporal do PLD, ou seja,
a ST não se desenvolve no tempo aleatoriamente ao redor de uma média μ constante, logo
não refletindo qualquer forma de equilíbrio estável (MORETTIN E TOLOI, 2006).
Figura 21 – Evolução do PLD Região SE/CO, Período de 2005 a 2010 (CP)
RESULTADOS OBTIDOS
55
Tendo em vista a não estacionariedade da série e com base na Equação (10),
transforma-se então esta série de preços em uma série de retornos, conforme Figura 22 a
seguir, possibilitando assim lidar com os modelos da família GARCH(p,q).
Figura 22 – Retornos da Série Temporal SE/CO de 2005 a 2010 (CP)
Constata-se visualmente na Figura 23 que um dos fatos estilizados na série de
retornos é o excesso de curtose, se comparado com a distribuição normal. Calculou-se a
curtose no R® usando a Equação (34) cujo valor obtido de 7,2 reputa-se alto.
=
(
(∑
− ̅)
( − ̅) )
(34)
Outro fato observado no histograma dos retornos exposto na Figura 23 é a presença
de caudas longas, típicas da existência de volatilidade.
Figura 23 – Histograma da Série Temporal SE/CO de 2005 a 2010 (CP)
RESULTADOS OBTIDOS
56
Na Figura 24 a seguir verifica-se a distribuição dos retornos, a função de
autocorrelação (ACF) e a função de autocorrelação parcial (PACF).
t)
2.0
1.0
0.0
Density
3.0
d e n s it y . d e f a u lt ( x = r
- 1 .5
- 1 .0
- 0 .5
0 .0
N
= 3 1 2
1 .0
1 .5
r t
0.0 0.2 0.4 0.6 0.8 1.0
S e r ie s
ACF
0 .5
B a n d w i d th = 0 .0 4 6 6 5
0
5
10
1 5
2 0
La g
-0.05
0.05
r t
-0.15
PartialACF
S e r ie s
5
1 0
1 5
2 0
La g
Figura 24 – Função Densidade, ACF e PACF dos Retornos (CP)
Embora as autocorrelações sejam pequenas, foram encontrados alguns valores
significativos para a autocorrelação (ACF) e autocorrelação parcial (PACF). Em vista desta
estrutura de dependência linear entre os retornos, deve-se antes ajustar um conjunto de 12
modelos ARIMA(p,d,q) para posteriormente modelar a volatilidade condicional.
6.1.1. Conjunto de modelos ARIMA(1,0,0) a (4,0,4)
Tabela 3 – Coeficientes Estimados dos Modelos ARIMA da ST do PLD (CP)
COEFICIENTES CALCULADOS
MODELO
AR1
AR2
AR3
AR4
MA1
MA2
MA3
ARIMA
-0.0214
(1,0,0)
0.0565
s.e.
-0.0268
(0,0,1)
0.0633
s.e.
0.9361
-1.0000
(1,0,1)
0.0211
0.0112
s.e.
-0.0237
-0.1007
(2,0,0)
0.0563
0.0562
s.e.
-0.0317
-0.1253
(0,0,2)
0.0570
0.0616
s.e.
-0.0084
0.8809
-0.0144
-0.9856
(2,0,2)
0.0350
0.0347
0.0188
0.0187
s.e.
-0.0241
-0.1008
-0.0037
(3,0,0)
0.0566
0.0562
0.0564
s.e.
-0.0329
-0.1329
-0.0341
(0,0,3)
0.0568
0.0617
0.0550
s.e.
-0.1800
0.1140
0.8725
0.1603
-0.2294
-0.9306
(3,0,3)
s.e.
0.0662
0.0507
0.0552
0.0646
0.0467
0.0627
(4,0,0)
-0.0244
-0.1116
-0.0063
-0.1044
s.e.
0.0563
0.0562
0.0561
0.0560
-0.0567
-0.1012
-0.0048
(0,0,4)
s.e.
0.0578
0.0594
0.0574
0.5339
-0.9855
0.2519
-0.7336
-0.5688
0.9270
-0.1784
(4,0,4)
0.2104
0.2328
0.2093
0.1301
0.2471
0.2752
0.2476
s.e.
Observaçoes: ɸ – Intercept,
– Valor Estimado e s.e. – Standard Error
(*) – Mensagem do R: Possível Problema na Convergência: optim retornou código=1
MA4
ɸ
-0.1160
0.0673
0.5898
0.1486
0.0035
0.0173
0.0035
0.0172
0.0019
0.0026
0.0036
0.0156
0.0037
0.0148
0.0019
0.0026
0.0037
0,0156
0.0038
0.0140
0,0019
0.0027
0.0038
0.0140
0.0040
0.0126
0.0034
0.0156
LLF
AIC
0.09714
-78.98
163.95
0.09713
-78.96
163.92
0.09399
-75.05
158.10
0.09614
-77.38
162.76
0.09588
-76.96
161.92
0.09240
-72.62
157.24
0.09614
-77.38
164.75
0.09576
-76.77
163.53
0.09178
-71.46
158.93
0.09507
-75.65
163.30
0.09487
-75.33
162.67
0.09026
-67.90
155.79
RESULTADOS OBTIDOS
57
Abaixo na Tabela 4 o resumo do conjunto de modelos ajustados, atenta-se para os
menores valores de AIC, LLF e δ dos modelos.
Tabela 4 – Resumo de Coeficientes e Critérios dos Modelos ARIMA Estimados
COEFICIENTES CALCULADOS
MODELO
ɸ
LLF
ARIMA
01
( 1, 0, 0)
0.0035
0.09714
-78.98
02
( 0, 0, 1)
0.0035
0.09713
-78.96
03
( 1, 0, 1)
0.0019
0.09399
-75.05
04
( 2, 0, 0)
0.0036
0.09614
-77.38
05
( 0, 0, 2)
0.0037
0.09588
-76.96
06
( 2, 0, 2)
0.0019
0.09240
-72.62
07
( 3, 0, 0)
0.0037
0.09614
-77.38
08
( 0, 0, 3)
0.0038
0.09576
-76.77
09
( 3, 0, 3)*
0.0019
0.09178
-71.46
10
( 4, 0, 0)
0.0038
0.09507
-75.65
11
( 0, 0, 4)
0.0040
0.09487
-75.33
12
( 4, 0, 4)
0.0034
0.09026
-67.90
Observações: ɸ – Intercept e
– Valor Estimado
(*) – Mensagem do R: Possível Problema na Convergência:
Optim retornou código=1
AIC
163.95
163.92
158.10
162.76
161.92
157.24
164.75
163.53
158.93
163.30
162.67
155.79
Escolhidos os modelos ARIMA(2,0,2) e ARIMA(4,0,4) em função de possuírem os
menores valores do critério AIC com 157,24 e 155,79 respectivamente.
6.1.2. Ajuste do GARCH com base no ARIMA(2,0,2)
Primeiramente utilizando os resíduos do modelo foram gerados gráficos dos
resíduos estandardizados, da ACF e do Teste Ljung-Box expostos na Figura 25. Verifica-se
então neste modelo que apesar de possuir valores pouco significativos no gráfico de ACF,
aparentemente eliminou-se a estrutura de autocorrelação entre os resíduos.
Figura 25 – Resíduos estandardizados, ACF e Teste Ljung-Box – ARIMA(2,0,2) (CP)
RESULTADOS OBTIDOS
58
Na sequência foram gerados na Figura 26 gráficos de ACF e PACF dos quadrados
dos resíduos, no objetivo de analisar as correlações e autocorrelações.
Figura 26 – ACF e PACF dos quadrados dos resíduos – ARIMA(2,0,2) (CP)
Percebe-se de forma clara a presença de efeitos ARCH/GARCH, visto que há uma
forte estrutura de autocorrelação no quadrado dos resíduos.
Em continuidade foram ajustados um conjunto de 3 modelos GARCH(p,q)
baseados na série de resíduos do modelo ARIMA(2,0,2) com os resultados na Tabela 5.
Tabela 5 – Estimação GARCH do Modelo ARIMA(2,0,2) Ajustado
BASE NO MODELO AJUSTADO ARIMA ( 2, 0 ,2 )
PARAMETRO
ESTIMATE
STD. ERROR
T VALUE
MIN
1Q
MEDIAN
3Q
-4.25022
-0.33183
0.01192
0.43653
GARCH(1,0)
a0
0.08807
3.47201
0.025
b1
0.05001
37.45347
0.001
-4.24266
-0.33168
0.01343
0.43970
a0
0.08372
NA
NA
GARCH(2,0)
b1
0.05004
NA
NA
b2
0.05004
NA
NA
-4.48292
-0.35848
0.01342
0.47830
a0
0.06844
0.01094
6.255
GARCH(1,1)
a1
0.22441
0.08438
2.660
b1
0.03328
0.12602
0.264
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
MODELO
PR(>|T|)
MAX
4.21360
0.980
0.999
4.20610
NA
NA
NA
4.75142
3.98e-10 ***
0.00782 **
0.79170
Os modelos GARCH(1,0) e GARCH(2,0) não foram adequados para descrever a
série, gerando problemas no procedimento de estimação. Na Tabela 6 a seguir estão
dispostos os resultados dos testes JB e LB dos modelos GARCH ajustados, cujos valores
não permitem rejeitar totalmente a hipótese de normalidade dos resíduos.
RESULTADOS OBTIDOS
59
Tabela 6 – Testes JB e LB da Estimação GARCH do Modelo ARIMA(2,0,2) Ajustado
MODELO
GARCH(1,0)
GARCH(2,0)
GARCH(1,1)
BASE NO MODELO AJUSTADO ARIMA ( 2, 0 ,2 )
JARQUE BERA
BOX-LJUNG
TEST RESIDUALS
TEST SQUARED RESIDUALS
X-SQUARED
DF
P-VALUE <
X-SQUARED
DF
P-VALUE <
154.1043
2
2.2e-16
22.2013
1
2.455e-06
151.7672
2
2.2e-16
22.0578
1
2.646e-06
200.7762
2
2.2e-16
0.0999
1
0.7519
Abaixo na Figura 27 os resíduos do modelo GARCH(1,1).
Figura 27 – Resíduos dos Retornos do Modelo GARCH(1,1) / ARIMA(2,0,2) (CP)
Utilizando a Figura 29, procede-se então a análise dos resíduos com base na ACF,
PACF e Histograma do modelo ajustado GARCH(1,1), mas como comparação exibe-se a
Figura 28 cuja série temporal de volatilidade menos agressiva foi também ajustada.
Figura 28 – ACF, PACF e Histograma de uma ST de Volatilidade Comportada (CP)
RESULTADOS OBTIDOS
60
Figura 29 – ACF, PACF e Histograma dos Resíduos GARCH(1,1)/ARIMA(2,0,2) (CP)
Ao analisar a Figura 28 de uma ST de volatilidade menos agressiva e com maior
número de observações (3000), nota-se a eliminação das autocorrelações e histograma
mais próximo da distribuição normal. Comparando-a com a Figura 29 do modelo ajustado
ARIMA(2,0,2) e GARCH(1,1) da ST do PLD, constata-se a persistência de
autocorrelações no gráfico da ACF, mesmo que mínimas, com histograma ainda pouco
diferente da normal, apesar de todos os ajustes efetuados. Elaboradas então no R® as
previsões, compostas por duas séries com a informação do desvio padrão, uma com sinais
positivos e a outra com sinais negativos, exibidos na Figura 30.
Figura 30 – Gráfico de Previsão do PLD Modelo GARCH(1,1) / ARIMA(2,0,2) (CP)
RESULTADOS OBTIDOS
61
6.1.3. Ajuste do GARCH com base no ARIMA(4,0,4)
O processo repete-se igualmente ao ARIMA(2,0,2), utilizando os resíduos do
modelo para gerar gráficos dos resíduos estandardizados, da ACF e do Teste Ljung-Box
expostos na Figura 31. Presentes neste modelo também valores pouco significativos no
gráfico de ACF, com aparente eliminação da estrutura de autocorrelação entre os resíduos.
Figura 31 – Resíduos estandardizados, ACF e Teste Ljung-Box – ARIMA(4,0,4) (CP)
Gerados em seguida gráficos de ACF e PACF dos quadrados dos resíduos exibidos
na Figura 32, onde constata-se a presença de efeitos ARCH/GARCH na PACF, e a
presença também de forte estrutura de autocorrelação no quadrado dos resíduos da ACF.
Figura 32 – ACF e PACF dos quadrados dos resíduos – ARIMA(4,0,4) (CP)
RESULTADOS OBTIDOS
62
Ajustados então um conjunto de 3 modelos GARCH(p,q) baseados na série de
resíduos do modelo ARIMA(4,0,4) com os resultados na Tabela 7 a seguir.
Tabela 7 – Estimação GARCH do Modelo ARIMA(4,0,4) Ajustado
BASE NO MODELO AJUSTADO ARIMA ( 4, 0 ,4 )
PARAMETRO
ESTIMATE
STD. ERROR
T VALUE
MIN
1Q
MEDIAN
3Q
-4.19777
-0.36845
-0.01176
0.37178
GARCH(1,0)
a0
0.08603
3.38806
0.025
b1
0.05003
37.41279
0.001
GARCH(2,0)
-4.19059
-0.36976
-0.01196
0.37283
a0
0.08178
NA
NA
b1
0.05003
NA
NA
b2
0.05003
NA
NA
-3.75515
-0.38626
-0.01491
0.40378
a0
0.014149
0.004898
2.889
GARCH(1,1)
a1
0.119475
0.047920
2.493
b1
0.726242
0.086730
8.374
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
MODELO
PR(>|T|)
MAX
4.25204
0.980
0.999
4.24477
NA
NA
NA
5.53357
0.00387 **
0.01266 *
2e-16 ***
Semelhantemente ao modelo ARIMA(2,0,2) anterior, os modelos GARCH(1,0) e
GARCH(2,0) não foram adequados para descrever a série, gerando problemas no
procedimento de estimação. Dispostos então na Tabela 8 os resultados dos testes JB e LB
dos modelos GARCH ajustados, cujos valores não nos permitem rejeitar totalmente a
hipótese de normalidade dos resíduos.
Tabela 8 – Testes JB e LB da Estimação GARCH do Modelo ARIMA(4,0,4) Ajustado
MODELO
GARCH(1,0)
GARCH(2,0)
GARCH(1,1)
BASE NO MODELO AJUSTADO ARIMA ( 4, 0 ,4 )
JARQUE BERA
BOX-LJUNG
TEST RESIDUALS
TEST SQUARED RESIDUALS
X-SQUARED
DF
P-VALUE <
X-SQUARED
DF
P-VALUE <
152.9241
2
2.2e-16
13.0582
1
0.000302
150.6140
2
2.2e-16
12.9557
1
0.000319
364.1482
2
2.2e-16
0.1908
1
0.662200
Na Figura 33 a seguir os resíduos do modelo GARCH(1,1) (ARIMA(4,0,4)).
Figura 33 – Resíduos dos Retornos do Modelo GARCH(1,1) / ARIMA(4,0,4) (CP)
RESULTADOS OBTIDOS
63
Figura 34 – ACF, PACF e Histograma dos Resíduos GARCH(1,1)/ARIMA(4,0,4) (CP)
Ao relembrar a Figura 28 de volatilidade comportada citada anteriormente e
comparando-a com a Figura 34 do modelo ajustado ARIMA(4,0,4) e GARCH(1,1) da ST
do PLD, constata-se, identicamente a anterior, a persistência de autocorrelações mínimas
também no gráfico da ACF, com o histograma ainda pouco diferente da normal e com
resquícios de caudas longas (-4 a 6), apesar de feitos todos os ajustes. Elaboradas então no
R® as previsões, compostas por duas séries com a informação do desvio padrão, uma com
sinais positivos e a outra com sinais negativos, exibidos na Figura 35.
Figura 35 – Gráfico de Previsão do PLD Modelo GARCH(1,1) / ARIMA(4,0,4) (CP)
RESULTADOS OBTIDOS
64
6.1.4. Resultados Obtidos Sem Outliers
Conforme exposto no Capítulo 4, subtítulo 4.1.4 efetuou-se modificações na série
temporal do PLD com vistas a minimizar os efeitos de outliers no objetivo de efetuar
melhores previsões. A seguir na Tabela 9 exibe-se o sumário estatístico da ST modificada.
Tabela 9 – Sumário Estatístico da ST do PLD no R® – Sem Outliers (CP)
SUMÁRIO ESTATÍSTICO DO R® - SEM OUTLIERS
Observações Mínimo Mediana Média
Máximo
313
12.80
52.97
71.44
309.60
Em sequência na Figura 36 a evolução da ST modificada.
Figura 36 – Gráfico da Série Temporal do PLD Sem Outliers (CP)
Os respectivos retornos da ST dispõem-se na Figura 37 abaixo.
Figura 37 – Gráfico dos Retornos do PLD Sem Outliers (CP)
RESULTADOS OBTIDOS
65
Em seguida na Figura 38 o histograma da ST modificada apresentando distribuição
leptocúrtica e caudas longas, típicos da presença de volatilidade.
Figura 38 – Histograma dos Retornos do PLD Sem Outliers (CP)
Após análise do gráfico de densidade, ACF e PACF dos retornos na Figura 39,
constata-se uma distribuição leptocúrtica com caudas longas típicos da volatilidade e
igualmente ao histograma anterior, permanência de pequenos valores de correlações e
estrutura típica ARCH, respectivamente.
Figura 39 – Densidade, ACF e PACF dos Retornos do PLD Sem Outliers (CP)
RESULTADOS OBTIDOS
66
6.1.5. Conjunto de modelos ARIMA(1,0,0) a (4,0,4) – Sem Outliers
Seguindo a mesma metodologia utilizada no tópico 6.1.1, inicialmente efetua-se
ajustes num conjunto de 12 modelos ARIMA(p,d,q) para posteriormente modelar a
volatilidade condicional.
Tabela 10 – Coeficientes Estimados dos Modelos ARIMA(1,0,0) a (4,0,4) Sem Outliers
COEFICIENTES CALCULADOS
(ST SEM OUTLIERS)
MODELO
AR1
AR2
AR3
AR4
MA1
MA2
MA3
ARIMA
-0.0457
(1,0,0)
0.0565
s.e.
-0.0570
(0,0,1)
0.0631
s.e.
0.9342
-1.0000
(1,0,1)
0.0213
0.0114
s.e.
-0.0504
-0.0994
(2,0,0)
0.0563
0.0562
s.e.
-0.0587
-0.1226
(0,0,2)
0.0569
0.0615
s.e.
-0.1841
0.7207
-0.1318
-0.8518
(2,0,2)
0.2215
0,2169
0.1814
0.1812
s.e.
-0.0510
-0.0997
-0.0059
(3,0,0)
0.0566
0.0563
0.0565
s.e.
-0.0597
-0.1276
-0.0311
(0,0,3)
0.0568
0.0614
0.0541
s.e.
0.0901
0.0040
0.7457
-0.1554
-0.1246
-0.7200
(3,0,3)
0.3114
0.2613
0.1214
0.3628
0.3064
0.1556
s.e.
-0.0515
-0.1098
-0.0111
-0.0987
(4,0,0)
0.0563
0.0563
0.0562
0.0561
s.e.
-0.0803
-0.0976
-0.0052
(0,0,4)
0.0574
0.0589
0.0566
s.e.
0.5639
-0.9677
0.2175
-0.6791
-0.6162
0.9314
-0.1538
(4,0,4)
0.2267
0.2427
0.2242
0.1659
0.2588
0.2806
0.2603
s.e.
Observaçoes: ɸ – Intercept e
Valor Estimado s.e. – Standard Error
(*) – Mensagem do R: Possível Problema na Convergência: optim retornou código=1
MA4
ɸ
-0.1112
0.0654
0.5357
0.1858
0.0036
0.0165
0.0036
0.0162
0.0019
0.0025
0.0037
0.0149
0.0037
0.0140
0.0043
0.0103
0.0037
0.0148
0.0038
0.0134
0.0019
0.0026
0.0038
0.0134
0.0040
0.0121
0.0034
0.0152
LLF
AIC
0.09265
-71.59
149.18
0.0926
-71.51
149.02
0.08971
-67.79
143,58
0.09172
-70.03
148.07
0.09146
-69.60
147.19
0.08919
-66.08
144.15
0.09172
-70.03
150.06
0.09136
-69.43
148.86
0.08811
-64.98
145.96
0.09080
-68.49
148.98
0.09054
-68.04
148.08
0.08689
-61.95
143.91
Resume-se na Tabela 11 o conjunto de modelos ajustados, observando-se
particularmente os menores valores de AIC, LLF e δ dos modelos.
Tabela 11 – Resumo de Coeficientes e Critérios dos Modelos ARIMA – Sem Outliers
COEFICIENTES CALCULADOS
(ST SEM OUTLIERS)
MODELO
ARIMA
01
02
03
04
05
06
07
08
09
10
11
12
ɸ
LLF
( 1, 0, 0)
0.0036
0.09265
-71.59
( 0, 0, 1)
0.0036
0.09260
-71.51
( 1, 0, 1)
0.0019
0.08971
-67.79
( 2, 0, 0)
0.0037
0.09172
-70.03
( 0, 0, 2)
0.0037
0.09146
-69.60
( 2, 0, 2)
0.0043
0.08919
-66.08
( 3, 0, 0)
0.0037
0.09172
-70.03
( 0, 0, 3)
0.0038
0.09136
-69.43
( 3, 0, 3)*
0.0019
0.08811
-64.98
( 4, 0, 0)
0.0038
0.09080
-68.49
( 0, 0, 4)
0.0040
0.09054
-68.04
( 4, 0, 4)
0.0034
0.08689
-61.95
Observaçoes: ɸ – Intercept e
Valor Estimado
(*) – Mensagem do R: Possível Problema na Convergência:
Optim retornou código=1
AIC
149.18
149.02
143,58
148.07
147.19
144.15
150.06
148.86
145.96
148.98
148.08
143.91
RESULTADOS OBTIDOS
67
6.1.6. Ajuste do GARCH com base no ARIMA – Sem Outliers
Escolhidos os modelos ARIMA (1,0,1), (2,0,2) e (4,0,4) dados os menores valores
dos critérios AIC, LLF e δ , procede-se a estimação e ajustes nos modelos GARCH.
Tabela 12 – Estimação GARCH do Modelo ARIMA(1,0,1) – Sem Outliers
MODELO
GARCH(1,0)
GARCH(2,0)
GARCH(1,1)
Signif. codes: 0
BASE NO MODELO AJUSTADO ARIMA ( 1, 0 ,1 )
(ST SEM OUTLIERS)
PARAMETRO
ESTIMATE
STD. ERROR
T VALUE
MIN
1Q
MEDIAN
3Q
-4.670913
-0.331412
-0.008201
0.411906
a0
0.08551
3.36997
0.025
b1
0.05001
37.44147
0.001
-4.662657
-0.331003
-0.008289
0.413061
a0
0.08129
NA
NA
b1
0.05004
NA
NA
b2
0.05004
NA
NA
-4.01052
-0.38903
-0.01099
0.42882
a0
0.013387
0.003559
3.762
a1
0.147349
0.049509
2.976
b1
0.706457
0.070473
10.025
‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
PR(>|T|)
MAX
4.333079
0.980
0.999
4.325421
NA
NA
NA
5.63022
0.000169 ***
0.002918 **
2e-16 ***
Tabela 13 – Testes JB e LB da Estimação GARCH / ARIMA(1,0,1) – Sem Outliers
MODELO
GARCH(1,0)
GARCH(2,0)
GARCH(1,1)
BASE NO MODELO AJUSTADO ARIMA ( 1, 0 ,1 )
(ST SEM OUTLIERS)
JARQUE BERA
BOX-LJUNG
TEST RESIDUALS
TEST SQUARED RESIDUALS
X-SQUARED
DF
P-VALUE <
X-SQUARED
DF
P-VALUE <
221.7048
2
2.2e-16
24.4675
1
7.557e-07
218.5471
2
2.2e-16
24.3229
1
8.146e-07
360.0757
2
2.2e-16
0.2624
1
0.6085
Após todos os ajustes efetuados foi gerada a previsão exibida na Figura 40 abaixo.
PREVISÃO DO PLD - SEM OUTLIERS
Series 2
0.5
0.4
-0.7 -0.6 -0.5 -0.4
-0.3 -0.2
0.2
0.3
Series 1
0.6
0.7
Região: SE/CO Patamar: Pesado - ARIMA(1,0,1) GARCH(1,1)
0
50
100
150
200
250
300
313 OBSERVAÇÕES ENTRE 2005 A 2010
Figura 40 – Gráfico de Previsão Modelo GARCH(1,1) / ARIMA(1,0,1) Sem Outliers
RESULTADOS OBTIDOS
68
Tabela 14 – Estimação GARCH do Modelo ARIMA(2,0,2) – Sem Outliers
MODELO
GARCH(1,0)
GARCH(2,0)
GARCH(1,1)
Signif. codes: 0
BASE NO MODELO AJUSTADO ARIMA ( 2, 0 ,2 )
(ST SEM OUTLIERS)
PARAMETRO
ESTIMATE
STD. ERROR
T VALUE
MIN
1Q
MEDIAN
3Q
-4.39701
-0.33480
-0.01842
0.39117
a0
0.08502
3.34843
0.025
b1
0.05003
37.41585
0.001
-4.38950
-0.33493
-0.01894
0.39104
a0
0.08082
NA
NA
b1
0.05003
NA
NA
b2
0.05003
NA
NA
-4.25185
-0.35549
-0.02243
0.38835
a0
0.014223
0.004441
3.203
a1
0.142595
0.052810
2.700
b1
0.702849
0.084040
8.363
‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
PR(>|T|)
MAX
4.38214
0.980
0.999
4.37465
NA
NA
NA
5.74613
0.00136 **
0.00693 **
2e-16 ***
Tabela 15 – Testes JB e LB da Estimação GARCH / ARIMA(2,0,2) – Sem Outliers
MODELO
GARCH(1,0)
GARCH(2,0)
GARCH(1,1)
BASE NO MODELO AJUSTADO ARIMA ( 2, 0 ,2 )
(ST SEM OUTLIERS)
JARQUE BERA
BOX-LJUNG
TEST RESIDUALS
TEST SQUARED RESIDUALS
X-SQUARED
DF
P-VALUE <
X-SQUARED
DF
P-VALUE <
188.0915
2
2.2e-16
17.6187
1
2.699e-05
185.3379
2
2.2e-16
17.4994
1
2.874e-05
445.8262
2
2.2e-16
0.0578
1
0.8100
Com todos os ajustes elaborados gerou-se a previsão exposta na Figura 41 a seguir.
Figura 41 – Gráfico de Previsão Modelo GARCH(1,1) / ARIMA(2,0,2) Sem Outliers
RESULTADOS OBTIDOS
69
Na estimação dos modelos ARIMA(4,0,4) GARCH(1,0) a (1,1) ocorreu falsa
convergência, motivo que inviabiliza a previsão.
Tabela 16 – Estimação GARCH do Modelo ARIMA(4,0,4) – Sem Outliers
MODELO
GARCH(1,0)
GARCH(2,0)
GARCH(1,1)
Signif. codes: 0
BASE NO MODELO AJUSTADO ARIMA ( 4, 0 ,4 )
(ST SEM OUTLIERS)
PARAMETRO
ESTIMATE
STD. ERROR
T VALUE
MIN
1Q
MEDIAN
3Q
-4.25186
-0.37840
-0.01259
0.34199
a0
0.08282
3.26322
0.025
b1
0.05003
37.42961
0.001
-4.24456
-0.37948
-0.01261
0.34176
a0
0.07873
NA
NA
b1
0.05003
NA
NA
b2
0.05003
NA
NA
-3.87900
-0.39003
-0.01531
0.38392
a0
0.013685
0.004251
3.219
a1
0.131723
0.050005
2.634
b1
0.713654
0.081427
8.764
‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
PR(>|T|)
MAX
4.32546
0.980
0.999
4.31803
NA
NA
NA
5.74257
0.00129 **
0.00843 **
2e-16 ***
Tabela 17 – Testes JB e LB da Estimação GARCH / ARIMA(4,0,4) – Sem Outliers
MODELO
GARCH(1,0)
GARCH(2,0)
GARCH(1,1)
BASE NO MODELO AJUSTADO ARIMA ( 4, 0 ,4 )
(ST SEM OUTLIERS)
JARQUE BERA
BOX-LJUNG
TEST RESIDUALS
TEST SQUARED RESIDUALS
X-SQUARED
DF
P-VALUE <
X-SQUARED
DF
P-VALUE <
184.626
2
2.2e-16
14.0812
1
0.0001751
181.9329
2
2.2e-16
13.9773
1
0.000185
474.6861
2
2.2e-16
0.0822
1
0.7743
6.2. RESULTADOS OBTIDOS NO EVIEWS®
No software estatístico Eviews®, gerou-se a Tabela 18 abaixo com dados
estatísticos da série temporal do PLD no período de 01/01/2005 a 31/12/2010 da região
SE/CO especificamente no patamar Pesado, cuja ST é a base aqui utilizada.
Tabela 18 – Sumário Estatístico da Série Temporal do PLD no Eviews®(CP)
SUMÁRIO ESTATÍSTICO DO EVIEWS®
Observações Mínimo Mediana Média Máximo
313
12.80
52.97
74.54
569,59
RESULTADOS OBTIDOS
70
Na Figura 42 exibe-se a ST do PLD especificamente da região SE/CO gerada no
software Eviews® na qual se efetuará os mesmos procedimentos utilizando a metodologia
Box-Jenkins explicitada anteriormente, todavia não serão minuciados novamente neste
subtítulo.
Gráfico da Evolução do PLD
Região: SE/CO Patamar: Pesado
600
500
R$/MWh
400
300
200
100
0
I
II
III IV
2005
I
II III IV
2006
I
II III IV
2007
I
II
III IV
I
2008
II
III IV
2009
I
II
III IV
2010
313 Observações de 2005 a 2010
Figura 42 – Evolução do PLD Região SE/CO, Período de 2005 a 2010 (CP)
Visto a não estacionariedade da ST conforme se constata na ACF e PACF da Figura
43, aplica-se a transformação para série de retornos exibidos na Figura 44 em sequência.
Figura 43 – Estatísticas ACF e PACF de SE/CO (CP)
RESULTADOS OBTIDOS
71
Transformação da ST de preços em série de retornos conforme Figura 44 abaixo.
Gráfico dos Retornos do PLD
Região: SE/CO Patamar: Pesado
1.5
1.0
0.5
0.0
-0.5
-1.0
-1.5
I
II
III IV
I
II
2005
III IV
2006
I
II
III IV
I
2007
II
III IV
I
II
2008
III IV
I
2009
II
III IV
2010
312 Observaç ões de 2005 a 2010
Figura 44 – Gráfico da Transformação ou Retornos da ST SE/CO (CP)
O histograma da série de retornos exibido na Figura 45 expõe as principais
características da presença da volatilidade, como distribuição leptocúrtica e caudas longas.
120
Series: LR_SECO
Sample 1/03/2005 12/27/2010
Observations 312
100
80
60
40
20
Mean
Median
Maximum
Minimum
Std. Dev.
Skewness
Kurtosis
0.001532
0.000000
0.604317
-0.608863
0.135606
0.195540
7.211060
Jarque-Bera
Probability
232.5176
0.000000
0
-0.6
-0.4
-0.2
0.0
0.2
0.4
0.6
Figura 45 – Histograma dos Retornos de SE/CO (CP)
Após os ajustes e estimação dos modelos escolheu-se o modelo GARCH(1,1) como
base para as previsões face ao menor valor AIC conforme exibido na Tabela 19 infra.
Tabela 19 – Critérios para escolha do modelo GARCH (CP)
BASE DO MODELO AJUSTADO ARIMA / GARCH
MODELO
AIC
SIC36
HQC37
RESULTADO
GARCH(1,0)-n 0.373331 0.421318 0.392510
Rejeitado
GARCH(1,1)-n 0.351238 0.411222 0.375211
Aceito
GARCH(2,0)-n 0.373477 0.433461 0.397451
Rejeitado
36
37
Schwartz Information Criterion.
Hannan-Quinn Criterion.
RESULTADOS OBTIDOS
72
A previsão com base no modelo GARCH(1,1) citado na Tabela 19 encontra-se na
Figura 46 abaixo, ressalta-se a semelhança com as previsões efetuadas no software R® na
Figura 35.
.6
.5
.4
.3
.2
.1
.0
I
II III IV
I
2005
II III IV
I
2006
II III IV
2007
I
II III IV I
II III IV
2008
2009
I
II III IV
2010
Condi t ional variance
Figura 46 – Gráfico de Previsão Modelo GARCH(1,1) da ST do PLD (CP)
Sendo que as estatísticas e as previsões positivas e negativas expõem-se
conjuntamente na Figura 47 a seguir.
1.5
Forecast: RT_SECOF
Actual: RT_SECO
Forecast sample: 1/07/2005 12/31/2010
Adjusted sample: 1/14/2005 12/31/2010
Included observations: 312
Root Mean Squared Error 0.311748
M ean Absol ute Error
0.192373
M ean Abs. Percent Error
81.28381
T hei l Inequal i ty Coeffi ci ent0.983049
Bi as Proporti on
0.000035
Vari ance Proportion
NA
Covariance Proporti on
NA
1.0
0.5
0.0
-0.5
-1.0
-1.5
2005
2006
2007
2008
RT_SECOF
2009
2010
± 2 S.E.
.6
.5
.4
.3
.2
.1
.0
2005
2006
2007
2008
2009
2010
Fo re ca s t o f Va ria n ce
Figura 47 – Gráficos de Previsões GARCH(1,1) e Estatísticas (CP)
RESULTADOS OBTIDOS
73
6.2.1. Resultados Obtidos Sem Outliers
Ratificando o exposto no Capítulo 4, subtítulo 4.1.4 efetivou-se modificações na
série temporal do PLD da Figura 48 no escopo de minimizar os efeitos de outliers com
vistas a obter melhores previsões. A Tabela 9 exibe o sumário estatístico da ST alterada.
Gráfico da Evolução do PLD - Sem Outliers
Região: SE/CO Patamar: Pesado
320
280
R$ / MWh
240
200
160
120
80
40
0
I
II
III IV
I
2005
II
III IV
2006
I
II
III IV
2007
I
II
III IV
I
II III IV
2008
I
2009
II
III IV
2010
313 Observações de 2005 a 2010
Figura 48 – Evolução do PLD Região SE/CO, Período 2005 a 2010 Sem Outliers (CP)
Visto a não estacionariedade da ST, aplica-se a transformação para série de retornos
expostos na Figura 49 abaixo.
Gráfico dos Retornos do PLD - Sem Outliers
Região: SE/CO Patamar: Pesado
1.5
1.0
0.5
0.0
-0.5
-1.0
-1.5
I
II III IV
2005
I
II III IV
2006
I
II III IV
2007
I
II III IV
I
2008
II III IV
2009
I
II III IV
2010
312 Observações de 2005 a 2010
Figura 49 – Retornos do PLD Região SE/CO, Período 2005 a 2010 Sem Outliers (CP)
RESULTADOS OBTIDOS
74
O histograma da série de retornos sem outliers exposto na Figura 50 exibe as
características da presença de volatilidade, como distribuição leptocúrtica e caudas longas.
120
Series: RTPLD_M
Sample 1/07/2005 12/31/2010
Observations 312
100
80
60
40
20
Mean
Median
Maximum
Minimum
Std. Dev.
Skewness
Kurtosis
0.003527
0.000000
1.391492
-1.401959
0.305187
0.263548
7.611730
Jarque-Bera
Probability
280.0965
0.000000
0
-1.5
-1.0
-0.5
0.0
0.5
1.0
Figura 50 – Histograma dos Retornos de SE/CO Sem Outliers (CP)
Em seguida aos ajustes e estimação dos modelos optou-se pelo GARCH(1,1) como
base das previsões face ao menor valor AIC exposto na Tabela 20 a seguir. Na sequência o
gráfico de previsão com base no modelo GARCH(1,1) referido na Tabela 20 e exibido na
Figura 51.
Tabela 20 – Critérios para escolha do modelo GARCH – Sem Outliers (CP)
BASE DO MODELO AJUSTADO ARIMA / GARCH - SO
MODELO
AIC
SIC38
HQC39
RESULTADO
GARCH(1,0)-n 0.407270 0.335289 0.378501
Rejeitado
GARCH(1,1)-n 0.363752 0.291772 0.334984
Aceito
GARCH(2,0)-n 0.434590 0.350612 0.401026
Rejeitado
Figura 51 – Gráfico de Previsão Modelo GARCH(1,1) da ST do PLD Sem Outliers (CP)
38
39
Schwartz Information Criterion.
Hannan-Quinn Criterion.
RESULTADOS OBTIDOS
75
O conjunto das estatísticas e as previsões positivas e negativas estão na Figura 52 a
seguir.
2
Forecast: RTPLD_MF
Actual: RTPLD_M
Forecast sample: 1/07/2005
Adjusted sample: 1/14/2005
Included observations: 312
Root Mean Squared Error
Mean Absolute Error
Mean Abs. Percent Error
Theil Inequality Coefficient
Bias Proportion
Variance Proportion
Covariance Proportion
1
0
-1
-2
2005
2006
2007
2008
RTPLD_MF
2009
2010
12/31/2010
12/31/2010
0.304718
0.186891
81.41026
1.000000
0.000134
NA
NA
± 2 S.E.
.6
.5
.4
.3
.2
.1
.0
2005
2006
2007
2008
2009
2010
Forecast of Variance
Figura 52 – Gráficos de Previsões GARCH(1,1) e Estatísticas Sem Outliers (CP)
6.3. ERROS DE PREVISÃO
Na Tabela 21 verificam-se os elevados valores de erros de previsão e a hegemonia
do GARCH(1,1) sobre outros modelos, bem como os melhores, porém pouco
significativos, ajustes no Eviews® e as alterações dos valores discrepantes ou Outliers.
Tabela 21 – Estimativas de Erros de Previsão (CP)
TABELA DE ERROS DE PREVISÃO
SOFTWARE
MODELO
MAE
RMSE
®
MAPE
0,218292 0,221328 104,7317
R
GARCH(1,1)
R®
GARCH(1,1) SO 0,215729 0,216249 102,7697
Eviews®
GARCH(1,1)
Eviews®
GARCH(1,1) SO 0,186891 0,304718 81,4103
Obs.: SO – Sem Outliers
0,192373 0,311748 81,2838
CONCLUSÕES
76
7. CONCLUSÕES
Nesta dissertação foram apresentadas as características principais e a singularidade
da commodity energia elétrica, uma breve explanação do funcionamento do mercado ACR
e ACL, considerando os impactos nos agentes e a precificação do PLD com o risco da
volatilidade inerente. Então com base em uma série temporal do período de 2005 a 2010
efetuaram-se análises estatísticas no escopo de detectar a existência da volatilidade,
determinar as características da série para a utilização de modelos heterocedásticos,
especificamente os modelos ARCH desenvolvido por Engle (1982) e a versão generalizada
por Bollerslev (1986) o GARCH.
Os modelos ARCH e GARCH foram descritos com as respectivas propriedades,
características e limitações sendo utilizados no objetivo de observar-se a melhor adequação
a série e consequentemente previsse com maior representatividade a volatilidade inerente
aos dados.
Sendo efetuadas diversas análises experimentais das variantes dos referidos
modelos, inclusive utilizando-se de softwares diferentes como o R® e Eviews® e com
resultados similares, cita-se que apesar da captura da variância condicionada, ou seja, da
volatilidade inerente, observou-se que quando das previsões o comportamento dos diversos
métodos de erros estimados não apresentavam resultados satisfatórios.
Conclui-se então uma baixa eficácia em utilizar os referidos modelos nesta série do
PLD visando obter previsões acuradas da volatilidade.
DIVULGAÇÃO DA PESQUISA
77
8. DIVULGAÇÃO DA PESQUISA
No decorrer do desenvolvimento deste trabalho e resultante de estágios desta
pesquisa foram publicados os seguintes artigos:
SOUSA, ANTONIO J. S.; VALENTE, ANDRÉ L. C. “Análise e Previsão da
Volatilidade do PLD Utilizando o Modelo GARCH”: XX Congreso
Internacional de Ingeniería Eléctrica, Electrónica, de Computación y Ramas
Afines – INTERCON 2013, Trujillo, Péru: v. 1 p. 1-7, de 05-09, Agosto, 2013
(Apresentado).
SOUSA, ANTONIO J. S.; VALENTE, ANDRÉ L. C. Tema: “Análise da Volatilidade
do Preço da Energia Elétrica no Mercado Brasileiro”: Área: Modelagem e
Predição de Séries Temporais, XI Simpósio Brasileiro de Automação
Inteligente – SBAI 2013 Fortaleza, CE, Brasil: v. 1 p. 1-6, de 13-17, Outubro,
2013 (Submetido: /br/realm/sbai-dincon-2013/submissions/6114).
SOUSA, ANTONIO J. S.; VALENTE, ANDRÉ L. C. Tema: Tema: “Previsão da
Volatilidade do PLD Utilizando o Modelo GARCH“: Área Modelagem e
Predição de Séries Temporais, XI Simpósio Brasileiro de Automação
Inteligente – SBAI 2013 Fortaleza, CE, Brasil: v. 1 p. 1-6, de 13-17, Outubro,
2013 (Submetido: /br/realm/sbai-dincon-2013/submissions/8316).
SUGESTÕES PARA TRABALHOS FUTUROS
78
9. SUGESTÕES PARA TRABALHOS FUTUROS
Considerando a altíssima volatilidade apresentada pela série do Preço de
Liquidação das Diferenças (PLD), estimulada pela concessão de larga margem de
oscilação, urge formas de minimizar tal margem no objetivo não só de melhor representar
o CMO, mas também de impor limites às descontroláveis oscilações que realmente não
representam os verdadeiros preços de custos momentâneos. Uma das formas seria a de
publicar diariamente o PLD, isto tenderia a aproximar a valoração do indicador ao custo
real da operação, minimizando a agressiva volatilidade atual.
Neste contexto seria promissora a utilização do modelo de Difusão de Saltos (Jump
Diffusion) ou ainda variações do GARCH (Bollerslev em 1986) mais recentes como o
GJR-GARCH (GJR - Glosten-Jagannathan-Runkle em 1993) ou o modelo quadrático
QGARCH (Sentana em 1995).
REFERÊNCIAS BIBLIOGRÁFICAS
79
10. REFERÊNCIAS BIBLIOGRÁFICAS
ABNT. NBR 15287, de 30 de dezembro de 2005. Norma que estabelece os princípios
gerais para apresentação de projetos de pesquisa. “Informação e documentação
– Projeto de pesquisa – Apresentação” Disponível em http://www.abnt.org.br/.
Acesso em 25 de maio de 2012.
ALMEIDA, LAUCIDES D. Gestão de Riscos Associados às Previsões de Demanda
das Distribuidoras de Energia Elétrica no Novo Contexto Regulatório
Brasileiro. Dissertação (Mestrado em Engenharia Elétrica) Salvador, Brasil.
UNIFACS. 2006.
BARROS, Mônica. Processos Estocásticos Editora, 2003 Disponível em
http://www.mbarros.com/documentos/upload/Livro_Processos_Cap_5_parte.pd
f', Último acesso em 05/10/2012 às 13:45 Hs.
BASTOS, PAULO R. F. M., Teoria de Portfólio Aplicada a Pequenas Centrais
Hidrelétricas. Dissertação (Mestrado em Engenharia Elétrica). Itajubá, Brasil:
Universidade Federal de Itajubá, 2002.
BOLLERSLEV, T., ENGLE, ROBERT F. (1993) “Common Persistence In Conditional
Variances” Econometrica, Vol. 61, No. 1 (January, 1993), pp. 167-186
BOLLERSLEV, TIM, (1986). “Generalized Auto-Regressive
Heteroskedasticity”, Journal of Econometrics, 31, pp. 307–327.
Conditional
BOX, G.E.P.; JENKINS, G.M.; REINSEL, G.C. “Time Series Analysis, Forecasting
and Control”, 3a Edição, Prentice Hall, 1994.
BRASIL. Decreto 5.081, de 14 de maio de 2004. Regulamenta os arts. 13 e 14 da Lei
no 9.648, de 27 de maio de 1998, e o art. 23 da Lei nº 10.848, de 15 de março
de 2004, que tratam do Operador Nacional do Sistema Elétrico – ONS.
Disponível em http://planalto.gov.br . Acesso em 25 de janeiro de 2012.
BRASIL. Decreto 5.163, de 30 de julho de 2004. Regulamenta a comercialização de
energia elétrica, o processo de outorga de concessões de autorizações de
geração de energia elétrica e outras providências. Disponível em
http://planalto.gov.br . Acesso em 25 de janeiro de 2012.
BRASIL. Decreto 5.175, de 09 de agosto de 2004. Constitui o Comitê de
Monitoramento do Setor Elétrico – CMSE de que trata o art. 14 da Lei
no 10.848, de 15 de março de 2004. Disponível em http://planalto.gov.br .
Acesso em 25 de janeiro de 2012.
REFERÊNCIAS BIBLIOGRÁFICAS
80
BRASIL. Decreto 5.177, de 12 de agosto de 2004. Regulamenta os arts. 4 e 5 da Lei
nº 10.848, de 15 de março de 2004, e dispõe sobre a organização, as atribuições
e o funcionamento da Câmara de Comercialização de Energia Elétrica – CCEE.
Disponível em http://planalto.gov.br . Acesso em 25 de janeiro de 2012.
BRASIL. Decreto 5.184, de 16 de agosto de 2004. Cria a Empresa de Pesquisa
Energética – EPE, aprova seu Estatuto Social e dá outras providências..
Disponível em http://planalto.gov.br . Acesso em 25 de janeiro de 2012.
BRASIL. Lei 10.433, de 24 de abril de 2002. Dispõe sobre a autorização para a
criação do Mercado Atacadista de Energia Elétrica – MAE. Disponível em
http://planalto.gov.br. Acesso em 25 de janeiro de 2012.
BRASIL. Lei 10.848, de 15 de março de 2004. Dispõe sobre a comercialização de
energia elétrica. Disponível em http://planalto.gov.br. Acesso em 25 de janeiro
de 2012.
BRASIL. Lei 9.074, de 07 de julho de 1995. Estabelece normas para outorga e
prorrogações das concessões e permissões de serviços públicos e dá outras.
Disponível em http://planalto.gov.br. Acesso em 25 de janeiro de 2012.
BROCKWELL, Peter J., DAVIS, Richard A., “Introduction to Times Series and
Forecasting”, 2a Edição, New York, USA, Printed Springer Inc., 2002.
BURATTI, R. M. Estratégia de contratação de energia para uma concessionária de
distribuição. Dissertação de Mestrado, Pontifícia Universidade Católica do
Paraná, Curitiba – PR, 2008.
CAMINADA, CARLOS, RAMOS, DOREL S., Estratégia de Contratação de
Consumidores Livres: Uma Análise Balizada Pela Formação de Preços No
Mercado Cativo. XIII ERIAC. Puerto Iguazú, Argentina, 2009.
CARDOSO, MAYRA M. Simulação de Modelos GARCH para Séries Temporais
Univariadas de Demanda de Energia Elétrica para Consumidores Livres em
Regime de Curto Prazo. Dissertação de Mestrado. Itajubá - MG, Brasil.
Universidade Federal de Itajubá, Itajubá, 2005.
CCEE. Câmara de Comercialização de Energia Elétrica.
http://www.ccee.org.br. Acesso em 25 de março de 2012.
Disponível em:
CCEE. Câmara de Comercialização de Energia Elétrica. Revista de Energia “CCEE
estuda publicar PLD diariamente” Disponível em: http://www.ccee.org.br.
http://www.mae.org.br: Acesso em 06 de agosto de 2013 às 09:45.
CEPEL Centro de Pesquisas de Energia Elétrica. Disponível em: http://www.ccee.
cepel.br/servicos/descprog.shtm. Acesso em 25 de março de 2012.
REFERÊNCIAS BIBLIOGRÁFICAS
81
D´ARAÚJO, ROBERTO P., Setor Elétrico Brasileiro Uma Aventura Mercantil.
Brasília, Brasil, CONFEA. 2009.
EHLERS, RICARDO S., Análise de Séries Temporais, Laboratório de Estatística e
Geoinformação – UFPR, Curitiba, Brasil: UFPR, 2003-2007.
ENGLE ROBERT F. (2001), “GARCH101: The Use of ARCH/GARCH Models in
Applied Econometrics”, Journal of Economic Perspectives, 15, pp. 157-168
ENGLE, ROBERT F. (1982). “Autoregressive conditional heteroskedasticity with
estimates of the U.K. inflation”. Econometrica, 50, pp. 987–1008.
ENGLE, ROBERT F., BOLLERSLEV, T., (1986) “Modelling the Persistence of
Conditional Variances” Departament of Econometrics, UCSD, La Jolla, CA –
USA
GUJARATI, DAMODAR N. Econometria Básica. 4ª edição, Rio de Janeiro, Brasil:
Editora Campus, 2006.
HATAMI, ALIREZA; et al. A Stochastic-Based Decision-Making Framework for an
Electricity Retailer: Time-of-use Pricing and Electricity Portfolio Optimization.
IEEE Transactions on Power Systems, Vol. 26, Nº. 4, November 2011.
LUBISCO, NÍDIA M L, et al. Manual de Estilo Acadêmico: Monografias, Dissertações
e Teses 4ª Edição Revista e Ampliada. Salvador, Brasil: EDUFBA, 2008.
LYRA, MARCOS S. Mitigação do Risco da Alta Volatilidade dos Preços da Energia
Elétrica no Mercado Australiano. Dissertação de Mestrado. Universidade
Federal do Ceará. Fortaleza, 2005.
MAYO, ROBERTO. Derivativos de Eletricidade & Gerenciamento de Risco. 1ª
Edição. Rio de Janeiro, Brasil: Editora Synergia, 2009.
MORETTIN, P.A., TOLOI, CÉLIA M., Análise de Séries Temporais. 2ª Edição. São
Paulo, Brasil: Editora Blucher, 2006.
RODRIGUES, RENATO D. B. Gerenciamento de risco no setor elétrico brasileiro
através do uso de derivativos. Dissertação de Mestrado. Rio de Janeiro, Brasil,
Universidade Federal do Rio de Janeiro. Rio de Janeiro, 2007.
SAMPAIO, LUCIANA L. Análise do Uso de Derivativos no Setor Elétrico Brasileiro.
Dissertação de Mestrado. Rio de Janeiro, Brasil. IBMEC, Rio de Janeiro, 2011.
SILVA, EDSON L. Formação de Preços em Mercados de Energia Elétrica. 1ª Edição.
Porto Alegre, Brasil: Editora Sagra Luzzatto, 2001.
REFERÊNCIAS BIBLIOGRÁFICAS
82
TOLMASQUIM, M. T. Novo Modelo do Setor Elétrico Brasileiro. 1ª Edição. Rio de
Janeiro, Brasil: Editora Synergia EPE, 2011.
WIENER, NORBERT. “Nonlinear problems in random theory”, The Technology
Press of Massachusetts Institute of Technology, 131 pp. 450, 1958.
YANG, YAN; et al. “Computing All Nash Equilibria Of Multiplayer Games In
Electricity Markets”. IEEE Transactions on Power Systems, Vol. 27, Nº. 1,
February 2012.
YULE, G. U. (1927). "On a Method of Investigating Periodicities in Disturbed Series,
with Special Reference to Wolfer's Sunspot Numbers". Philosophical
Transactions of the Royal Society A: Mathematical, Physical and Engineering
Sciences 226 (636–646): 267–226.
ANEXO
83
ANEXO I
Série Temporal – PLD:
SE / CO
SÉRIE ORIGINAL
07/01/2005 A
31/12/2010
DATA
R$
07/01/2005 18,33
14/01/2005 18,33
21/01/2005 18,33
28/01/2005 18,33
04/02/2005 18,33
11/02/2005 18,33
18/02/2005 18,33
25/02/2005 18,33
04/03/2005 18,33
11/03/2005 18,33
18/03/2005 18,33
25/03/2005 18,33
01/04/2005 18,33
08/04/2005 18,33
15/04/2005 20,17
22/04/2005 26,11
29/04/2005 34,76
06/05/2005 48,82
13/05/2005 42,25
20/05/2005 49,45
27/05/2005 46,00
03/06/2005 28,91
10/06/2005 18,33
17/06/2005 31,80
24/06/2005 31,22
01/07/2005 24,99
08/07/2005 27,18
15/07/2005 33,28
22/07/2005 36,24
29/07/2005 34,83
05/08/2005 29,62
12/08/2005 27,93
19/08/2005 38,55
26/08/2005 34,13
02/09/2005 48,35
09/09/2005 40,76
16/09/2005 33,33
23/09/2005 29,29
30/09/2005 24,55
07/10/2005 39,27
14/10/2005 43,27
21/10/2005 45,21
28/10/2005 52,97
04/11/2005 50,80
11/11/2005 33,64
18/11/2005 34,69
25/11/2005 38,11
02/12/2005 33,38
09/12/2005 18,33
16/12/2005 18,33
23/12/2005
30/12/2005
06/01/2006
13/01/2006
20/01/2006
27/01/2006
03/02/2006
10/02/2006
17/02/2006
24/02/2006
03/03/2006
10/03/2006
17/03/2006
24/03/2006
31/03/2006
07/04/2006
14/04/2006
21/04/2006
28/04/2006
05/05/2006
12/05/2006
19/05/2006
26/05/2006
02/06/2006
09/06/2006
16/06/2006
23/06/2006
30/06/2006
07/07/2006
14/07/2006
21/07/2006
28/07/2006
04/08/2006
11/08/2006
18/08/2006
25/08/2006
01/09/2006
08/09/2006
15/09/2006
22/09/2006
29/09/2006
06/10/2006
13/10/2006
20/10/2006
27/10/2006
03/11/2006
10/11/2006
17/11/2006
24/11/2006
01/12/2006
08/12/2006
15/12/2006
22/12/2006
29/12/2006
05/01/2007
18,33
18,33
16,92
16,92
16,92
40,46
68,78
62,84
86,64
37,78
40,00
40,60
16,92
16,92
39,35
24,21
22,14
18,02
16,92
37,52
50,04
57,27
56,42
60,32
63,09
65,44
75,23
75,36
93,90
89,97
86,57
92,65
108,13
101,83
103,35
102,42
129,69
128,18
120,75
131,59
132,63
110,38
115,24
82,89
82,37
70,68
94,81
68,99
79,56
86,09
79,07
71,10
53,09
37,55
37,75
12/01/2007
19/01/2007
26/01/2007
02/02/2007
09/02/2007
16/02/2007
23/02/2007
02/03/2007
09/03/2007
16/03/2007
23/03/2007
30/03/2007
06/04/2007
13/04/2007
20/04/2007
27/04/2007
04/05/2007
11/05/2007
18/05/2007
25/05/2007
01/06/2007
08/06/2007
15/06/2007
22/06/2007
29/06/2007
06/07/2007
13/07/2007
20/07/2007
27/07/2007
03/08/2007
10/08/2007
17/08/2007
24/08/2007
31/08/2007
07/09/2007
14/09/2007
21/09/2007
28/09/2007
05/10/2007
12/10/2007
19/10/2007
26/10/2007
02/11/2007
09/11/2007
16/11/2007
23/11/2007
30/11/2007
07/12/2007
14/12/2007
21/12/2007
28/12/2007
04/01/2008
11/01/2008
18/01/2008
25/01/2008
28,16
17,59
17,59
17,59
17,59
17,59
17,59
17,59
17,59
17,59
17,59
17,59
17,59
63,65
54,30
57,74
55,15
37,63
45,44
50,93
122,91
105,40
119,13
78,70
84,72
139,36
142,69
133,41
120,18
61,74
29,98
29,25
35,19
59,40
129,18
132,65
150,11
189,13
168,46
173,85
207,66
211,84
237,66
224,10
182,68
150,54
170,27
189,25
212,20
200,48
199,76
247,01
475,53
569,59
569,59
01/02/2008
08/02/2008
15/02/2008
22/02/2008
29/02/2008
07/03/2008
14/03/2008
21/03/2008
28/03/2008
04/04/2008
11/04/2008
18/04/2008
25/04/2008
02/05/2008
09/05/2008
16/05/2008
23/05/2008
30/05/2008
06/06/2008
13/06/2008
20/06/2008
27/06/2008
04/07/2008
11/07/2008
18/07/2008
25/07/2008
01/08/2008
08/08/2008
15/08/2008
22/08/2008
29/08/2008
05/09/2008
12/09/2008
19/09/2008
26/09/2008
03/10/2008
10/10/2008
17/10/2008
24/10/2008
31/10/2008
07/11/2008
14/11/2008
21/11/2008
28/11/2008
05/12/2008
12/12/2008
19/12/2008
26/12/2008
02/01/2009
09/01/2009
16/01/2009
23/01/2009
30/01/2009
06/02/2009
13/02/2009
550,28
256,05
124,75
163,45
217,48
140,14
135,26
179,91
80,48
88,21
121,95
70,01
48,74
42,11
29,66
15,47
34,77
51,62
76,89
77,02
71,74
77,73
89,07
91,79
103,31
111,69
147,75
140,43
121,54
81,49
74,29
96,02
109,04
122,97
126,19
101,80
98,98
76,91
94,07
100,76
105,42
120,15
113,85
93,74
97,08
103,56
113,15
91,74
74,16
28,13
62,66
140,66
110,71
65,40
75,61
ANEXO
20/02/2009 66,27
27/02/2009 16,31
06/03/2009 65,58
13/03/2009 84,39
20/03/2009 109,29
27/03/2009 101,79
03/04/2009 108,31
10/04/2009 49,38
17/04/2009 51,64
24/04/2009 40,24
01/05/2009 46,66
08/05/2009 46,98
15/05/2009 36,89
22/05/2009 37,29
29/05/2009 37,87
05/06/2009 38,48
12/06/2009 35,14
19/06/2009 41,54
26/06/2009 43,11
03/07/2009 51,96
10/07/2009 39,62
17/07/2009 31,78
24/07/2009 21,00
31/07/2009 21,67
07/08/2009 16,31
84
14/08/2009
21/08/2009
28/08/2009
04/09/2009
11/09/2009
18/09/2009
25/09/2009
02/10/2009
09/10/2009
16/10/2009
23/10/2009
30/10/2009
06/11/2009
13/11/2009
20/11/2009
27/11/2009
04/12/2009
11/12/2009
18/12/2009
25/12/2009
01/01/2010
08/01/2010
15/01/2010
22/01/2010
29/01/2010
16,31
16,31
16,31
16,31
16,31
16,31
16,31
16,31
16,31
16,31
16,31
16,31
16,31
16,31
16,31
16,31
16,31
16,31
16,31
16,31
16,31
12,80
12,80
12,80
12,80
05/02/2010 12,80
12/02/2010 12,80
19/02/2010 12,80
26/02/2010 12,80
05/03/2010 33,29
12/03/2010 17,70
19/03/2010 25,99
26/03/2010 36,72
02/04/2010 38,83
09/04/2010 26,76
16/04/2010 12,80
23/04/2010 24,81
30/04/2010 24,00
07/05/2010 25,16
14/05/2010 30,27
21/05/2010 33,77
28/05/2010 36,25
04/06/2010 58,07
11/06/2010 61,38
18/06/2010 60,48
25/06/2010 66,05
02/07/2010 103,36
09/07/2010 104,59
16/07/2010 100,03
23/07/2010 86,60
30/07/2010
06/08/2010
13/08/2010
20/08/2010
27/08/2010
03/09/2010
10/09/2010
17/09/2010
24/09/2010
01/10/2010
08/10/2010
15/10/2010
22/10/2010
29/10/2010
05/11/2010
12/11/2010
19/11/2010
26/11/2010
03/12/2010
10/12/2010
17/12/2010
24/12/2010
31/12/2010
79,16
107,23
128,74
120,23
125,73
111,40
137,60
122,46
139,53
170,74
149,09
124,99
146,88
145,43
149,48
121,71
128,58
103,41
81,79
92,88
78,04
66,99
55,09
ANEXO
SE/CO
SÉRIE
DIFERENCIADA
07/01/2005 A
31/12/2010
DATA
R$
1/07/2005
NA
1/14/2005
0.00
1/21/2005
0.00
1/28/2005
0.00
2/04/2005
0.00
2/11/2005
0.00
2/18/2005
0.00
2/25/2005
0.00
3/04/2005
0.00
3/11/2005
0.00
3/18/2005
0.00
3/25/2005
0.00
4/01/2005
0.00
4/08/2005
0.00
4/15/2005
1.84
4/22/2005
5.94
4/29/2005
8.65
5/06/2005
14.06
5/13/2005
-6.57
5/20/2005
7.20
5/27/2005
-3.45
6/03/2005 -17.09
6/10/2005 -10.58
6/17/2005
13.47
6/24/2005
-0.58
7/01/2005
-6.23
7/08/2005
2.19
7/15/2005
6.10
7/22/2005
2.96
7/29/2005
-1.41
8/05/2005
-5.21
8/12/2005
-1.69
8/19/2005
10.62
8/26/2005
-4.42
9/02/2005
14.22
9/09/2005
-7.59
9/16/2005
-7.43
9/23/2005
-4.04
9/30/2005
-4.74
10/07/2005 14.72
10/14/2005
4.00
10/21/2005
1.94
10/28/2005
7.76
11/04/2005 -2.17
11/11/2005 -17.16
11/18/2005
1.05
11/25/2005
3.42
12/02/2005 -4.73
12/09/2005 -15.05
12/16/2005
0.00
85
12/23/2005
12/30/2005
1/06/2006
1/13/2006
1/20/2006
1/27/2006
2/03/2006
2/10/2006
2/17/2006
2/24/2006
3/03/2006
3/10/2006
3/17/2006
3/24/2006
3/31/2006
4/07/2006
4/14/2006
4/21/2006
4/28/2006
5/05/2006
5/12/2006
5/19/2006
5/26/2006
6/02/2006
6/09/2006
6/16/2006
6/23/2006
6/30/2006
7/07/2006
7/14/2006
7/21/2006
7/28/2006
8/04/2006
8/11/2006
8/18/2006
8/25/2006
9/01/2006
9/08/2006
9/15/2006
9/22/2006
9/29/2006
10/06/2006
10/13/2006
10/20/2006
10/27/2006
11/03/2006
11/10/2006
11/17/2006
11/24/2006
12/01/2006
12/08/2006
12/15/2006
12/22/2006
12/29/2006
1/05/2007
1/12/2007
0.00
0.00
-1.41
0.00
0.00
23.54
28.32
-5.94
23.80
-48.86
2.22
0.60
-23.68
0.00
22.43
-15.14
-2.07
-4.12
-1.10
20.60
12.52
7.23
-0.85
3.90
2.77
2.35
9.79
0.13
18.54
-3.93
-3.40
6.08
15.48
-6.30
1.52
-0.93
27.27
-1.51
-7.43
10.84
1.04
-22.25
4.86
-32.35
-0.52
-11.69
24.13
-25.82
10.57
6.53
-7.02
-7.97
-18.01
-15.54
0.20
-9.59
1/19/2007
1/26/2007
2/02/2007
2/09/2007
2/16/2007
2/23/2007
3/02/2007
3/09/2007
3/16/2007
3/23/2007
3/30/2007
4/06/2007
4/13/2007
4/20/2007
4/27/2007
5/04/2007
5/11/2007
5/18/2007
5/25/2007
6/01/2007
6/08/2007
6/15/2007
6/22/2007
6/29/2007
7/06/2007
7/13/2007
7/20/2007
7/27/2007
8/03/2007
8/10/2007
8/17/2007
8/24/2007
8/31/2007
9/07/2007
9/14/2007
9/21/2007
9/28/2007
10/05/2007
10/12/2007
10/19/2007
10/26/2007
11/02/2007
11/09/2007
11/16/2007
11/23/2007
11/30/2007
12/07/2007
12/14/2007
12/21/2007
12/28/2007
1/04/2008
1/11/2008
1/18/2008
1/25/2008
2/01/2008
2/08/2008
-10.57
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
46.06
-9.35
3.44
-2.59
-17.52
7.81
5.49
71.98
-17.51
13.73
-40.43
6.02
54.64
3.33
-9.28
-13.23
-58.44
-31.76
-0.73
5.94
24.21
69.78
3.47
17.46
39.02
-20.67
5.39
33.81
4.18
25.82
-13.56
-41.42
-32.14
19.73
18.98
22.95
-11.72
-0.72
47.25
228.52
94.06
0.00
-19.31
-294.23
2/15/2008
2/22/2008
2/29/2008
3/07/2008
3/14/2008
3/21/2008
3/28/2008
4/04/2008
4/11/2008
4/18/2008
4/25/2008
5/02/2008
5/09/2008
5/16/2008
5/23/2008
5/30/2008
6/06/2008
6/13/2008
6/20/2008
6/27/2008
7/04/2008
7/11/2008
7/18/2008
7/25/2008
8/01/2008
8/08/2008
8/15/2008
8/22/2008
8/29/2008
9/05/2008
9/12/2008
9/19/2008
9/26/2008
10/03/2008
10/10/2008
10/17/2008
10/24/2008
10/31/2008
11/07/2008
11/14/2008
11/21/2008
11/28/2008
12/05/2008
12/12/2008
12/19/2008
12/26/2008
1/02/2009
1/09/2009
1/16/2009
1/23/2009
1/30/2009
2/06/2009
2/13/2009
2/20/2009
2/27/2009
3/06/2009
-131.30
38.70
54.03
-77.34
-4.88
44.65
-99.43
7.73
33.74
-51.94
-21.27
-6.63
-12.45
-14.19
19.30
16.85
25.27
0.13
-5.28
5.99
11.34
2.72
11.52
8.38
36.06
-7.32
-18.89
-40.05
-7.20
21.73
13.02
13.93
3.22
-24.39
-2.82
-22.07
17.16
6.69
4.66
14.73
-6.30
-20.11
3.34
6.48
9.59
-21.41
-17.58
-46.03
34.53
78.00
-29.95
-45.31
10.21
-9.34
-49.96
49.27
ANEXO
3/13/2009
3/20/2009
3/27/2009
4/03/2009
4/10/2009
4/17/2009
4/24/2009
5/01/2009
5/08/2009
5/15/2009
5/22/2009
5/29/2009
6/05/2009
6/12/2009
6/19/2009
6/26/2009
7/03/2009
7/10/2009
7/17/2009
7/24/2009
7/31/2009
8/07/2009
8/14/2009
8/21/2009
86
18.81
24.90
-7.50
6.52
-58.93
2.26
-11.40
6.42
0.32
-10.09
0.40
0.58
0.61
-3.34
6.40
1.57
8.85
-12.34
-7.84
-10.78
0.67
-5.36
0.00
0.00
8/28/2009
9/04/2009
9/11/2009
9/18/2009
9/25/2009
10/02/2009
10/09/2009
10/16/2009
10/23/2009
10/30/2009
11/06/2009
11/13/2009
11/20/2009
11/27/2009
12/04/2009
12/11/2009
12/18/2009
12/25/2009
1/01/2010
1/08/2010
1/15/2010
1/22/2010
1/29/2010
2/05/2010
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
-3.51
0.00
0.00
0.00
0.00
2/12/2010
2/19/2010
2/26/2010
3/05/2010
3/12/2010
3/19/2010
3/26/2010
4/02/2010
4/09/2010
4/16/2010
4/23/2010
4/30/2010
5/07/2010
5/14/2010
5/21/2010
5/28/2010
6/04/2010
6/11/2010
6/18/2010
6/25/2010
7/02/2010
7/09/2010
7/16/2010
7/23/2010
0.00
0.00
0.00
20.49
-15.59
8.29
10.73
2.11
-12.07
-13.96
12.01
-0.81
1.16
5.11
3.50
2.48
21.82
3.31
-0.90
5.57
37.31
1.23
-4.56
-13.43
7/30/2010
8/06/2010
8/13/2010
8/20/2010
8/27/2010
9/03/2010
9/10/2010
9/17/2010
9/24/2010
10/01/2010
10/08/2010
10/15/2010
10/22/2010
10/29/2010
11/05/2010
11/12/2010
11/19/2010
11/26/2010
12/03/2010
12/10/2010
12/17/2010
12/24/2010
12/31/2010
-7.44
28.07
21.51
-8.51
5.50
-14.33
26.20
-15.14
17.07
31.21
-21.65
-24.10
21.89
-1.45
4.05
-27.77
6.87
-25.17
-21.62
11.09
-14.84
-11.05
-11.90