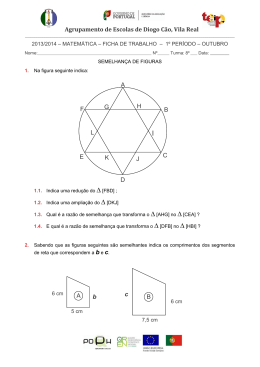
Escola Secundária com 3ºCiclo do Ensino Básico de Tondela
Ano Lectivo 2006/2007
Semelhança de Triângulos
8º Ano
Tarefa 1: Polígonos semelhantes (com o Cabri – Géomètre)
1.
a) Construa um triângulo [ABC].
b) Construa outro triângulo [DEF], com os lados paralelos aos lados de [ABC].
c) Meça as amplitudes dos ângulos internos desses triângulos e os comprimentos dos
seus lados. Que relações pode estabelecer entre estes triângulos que lhe permitam
afirmar que são semelhantes?
d) Qual a razão de semelhança?
e) Arraste um dos vértices do triângulo [ABC] e verifique se as relações que
estabeleceu na alínea c) se mantêm.
2.
a) Construa dois quadriláteros semelhantes.
b) Que razões lhe permitem afirmar que são semelhantes?
Explique as medições que efectuou e as relações que encontrou que justificam que
esses quadriláteros são semelhantes.
3.
a) Construa um quadrilátero qualquer.
b) Construa um quadrilátero semelhante ao inicial de razão 0,5 utilizando somente
os comandos do Cabri, Ponto Médio e Recta Paralela.
c) Utilize apenas os mesmos comandos para construir dois pentágonos semelhantes
de razão 0,5.
Escola Secundária com 3ºCiclo do Ensino Básico de Tondela
Ano Lectivo 2006/2007
Semelhança de Triângulos
8º Ano
Tarefa 2: Razões de semelhança: perímetros e áreas
(com o Cabri – Géomètre)
1.
a) Construa uma figura como a seguinte, onde:
A1 é ponto médio de [A C] e B1 é ponto médio de [B C]
A2 é ponto médio de [A1 C] e B2 é ponto médio de [B1 C]
E assim sucessivamente…
b) Todos os triângulos que fazem parte desta figura são semelhantes.
Justifique esta afirmação, efectuando se necessário algumas medições.
c) Preencha a tabela abaixo:
Triângulos
[A3 B3 C]
[A2 B2 C]
[A1 B1 C]
[A B C]
Perímetro
Área
d) Consegue estabelecer alguma relação entre os perímetros dos vários triângulos? A
razão de semelhança ajuda a explicar estas relações?
e) Consegue estabelecer alguma relação entre as áreas dos vários triângulos? A razão
de semelhança ajuda a explicar estas relações?
f) Se arrastar um dos vértices do triângulo [ABC], estas relações mantêm-se?
g) Se quisesse construir um triângulo semelhante ao triângulo [A3 B3 C] mas com a
área 9 vezes maior, como é que procederia?
h) Tente construí-lo com a ajuda do Cabri-Géomètre e mostre que a área desse novo
triângulo tem a medida que desejava.