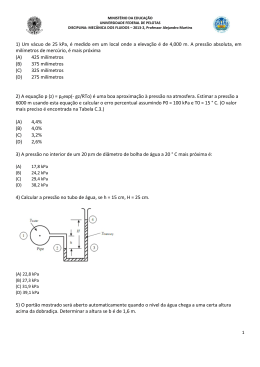
Helder Anibal Hermini
1
2
 Equação geral dos gases
 A Expansibilidade dos gases (Lei de BoyleMariotte)
 Variação do Volume em função da Temperatura
(Lei de Gay-Lussac)
 Cálculo de volume de reservatório quando a
regulagem é intermitente
 Cálculo da tubulação da rede distribuidora
3
Unidades básicas
Unidades derivadas
4
F=m.a
1 kgf = 1 kp = 9,81 N=2,202 Lbf
5
N
1 Pa  1 2
m
kgf
1 bar  1
2
cm
Lbf
1 PSI  1
2
Pol
Sistema Internacio nal 
MKS 
*
Sistema Inglês 
6
1 Bar

14,2 PSI

105 Pa
7
Para todos os gases é válida a “Equação Geral dos Gases”
P1.V1 P2 .V2

T1
T2
8
9
Sob a temperatura constante, o volume de um gás
fechado em um recipiente é inversamente proporcional à
pressão absoluta, quer dizer, o produto da pressão
absoluta e o volume é constante para uma determinada
quantidade de gás.
P1.V1  P2 .V2  P3.V3  constante
10
Exemplo 1: Um volume v1 = 1 m3, sob pressão atmosférica p1 = 100 kPa (1bar)
é reduzido pela força F2 para um volume V2 = 0,5 m3; mantendo-se a
temperatura constante, a pressão resultante será:
P1.V1  P2 .V2
P2 
P1.V1
V2
100 kP a. 1 m 3
P2 
 200 kP a (2 bar)
0,5 m 3
Se o volumeV1 for comprimidopela força F3 para um volumeV3  0,05 m 3 , a
pressão result ant eserá :
P .V
P3  1 1
V3
100 kP a. 1 m 3
P3 
 2000kP a (20 bar)
3
0,05m
11
12
Se a pressão permanece constante e a temperatura
se eleva 1 K partindo de 273 K, o ar se dilata 1 / 273 do seu
volume. Isto é demonstrado pela lei da Gay-Lussac.
V1 T1

V2 T2
V1
T2  T1 
V2  V1 
T1
Para temperaturas em Kelvin
V1
T2  T1 
V2  V1 
273 T1
Para temperaturas em Celsius
13
Exemplo 2: 0,8 m3 de ar com temperatura T1 = 293 K
(20o C), será aquecido para T2 = 344 K (71o C) . Calcular
o volume final.
3
0,8 m
344 K  293K 
V2  0,8 m 
293 K
3
3
3
V2  0,8 m  0,14 m  0,94 m
3
3
3
O ar se dilat a de 0,14 m a 0,94 m .
14
15
Exemplo 3: Dimensionar o volume de um reservatório
para um sistema cujo:
Consumo
Q = 20 m3 / min
Interrupções / hora
Z = 20
Diferencial de pressão
p = 100 kPa (1 bar)
Volume do Reservatório
Vb = ?
16
Consumo
Q = 20 m3 / min

Diferencial de pressão
p = 100 kPa (1 bar)

Interrupções / hora
Z = 20

Volume do Reservatório Vb
= 15 m3
17
18
Exemplo 4: O consumo de ar em uma indústria é de 4
m3 / min. (240 m3 / hora). O aumento em três anos será
de 300 %. Isso resultará num consumo de 12 m3 / min.
(720 m3 / hora).
O consumo total é estipulado em 16 m3 / min. (960 m3 /
hora). A tubulação terá um comprimento de 280 m; esta
rede possuirá 6 peças em “T”, 5 cotovelos normais, e 1
válvula de passagem. A queda de pressão admissível é de
p = 10 kPa (0,1 bar). A pressão na rede deverá ser de
800 kPa (8bar).
Calcular o diâmetro do tubo.
19
Com os dados do
exemplo 4 será
determinado
no
monograma
o
diâmetro do tubo.
20
1o Passo
Unir o valor da
coluna A (comprimento da
tubulação = 280 m), com o
valor da coluna B (consumo
de ar = 960 m3 / hora) com
um traço, prolongando até a
coluna C (eixo 1 de
referência) obtendo um
ponto de intersecção.
21
2o Passo
Unir a coluna E
(pressão = 800 kPa (8bar). ),
com o valor da coluna G
(queda de pressão = p = 10
kPa (0,1 bar)) passando por
cima da coluna F (eixo 2 de
referência),
obtendo-se
então,
um
ponto
de
intersecção.
22
3o Passo
Pelos pontos dos eixos
1 e 2 passar um traço
unindo-os
e
obtendo-se
assim,
na
coluna
D
(diâmetro do tubo), um valor
inicial da tubulação.
Neste caso, se obtém um
valor inicial de 90 mm de
diâmetro para a tubulação.
23
Para os elementos estranguladores do fluxo
(válvulas de gaveta, de passagem, de assento,
peças em “T”, cotovelos, etc.), as resistências são
transformadas em comprimento equivalente.
Como comprimento equivalente compreende-se o
comprimento linear de tubo reto, cuja resistência
à passagem do ar seja igual à resistência oferecida
pelo elemento em questão.
A secção transversal do tubo de
“comprimento equivalente” é a mesma do tubo
24
utilizado na rede.
Por
meio
do
monograma 2 poderão ser
determinados os comprimentos
equivalentes.
25
Comprimento equivalente conforme o monograma 2
Comprimento equivalente conforme o monograma 2
6 peças “T” (90 mm)
= 6 . 10,5 m = 63 m
1 válvula de passagem (90 mm) =
5 cotovelos normais (90 mm)
= 5. 1 m =
32 m
5m
___________________________________________
Comprimento equivalente
100 m
Comprimento da tubulação
280 m
Comprimento equivalente
100 m
___________________________________________
Comprimento total
380 m
26
Com este comprimento
total de tubulação (380 m), o
consumo de ar, a queda de
pressão e a pressão de
trabalho, pode-se determinar,
no monograma 1, o diâmetro
real necessário.
27
Consumo total = 16 m3 / min. (960 m3 / hora)
Comprimento total de tubulação = 380 m
Queda de pressão = p = 10 kPa (0,1 bar)
Pressão na rede = 800 kPa (8bar)
28
1o Passo
Unir o valor da
coluna A (comprimento da
tubulação = 380 m), com o
valor da coluna B (consumo
de ar = 16 m3 / min. (960 m3 /
hora)) com um traço,
prolongando até a coluna C
(eixo 1 de referência)
obtendo um ponto de
intersecção.
29
2o Passo
Unir a coluna E (pressão
= 800 kPa (8bar)), com o valor da
coluna G (queda de pressão p =
10 kPa (0,1 bar)) passando por
cima da coluna F (eixo 2 de
referência), obtendo-se então, um
ponto de intersecção.
30
3o Passo
Pelos pontos dos eixos
1 e 2 passar um traço
unindo-os
e
obtendo-se
assim o diâmetro do tubo
para este exemplo de 95 mm.
31