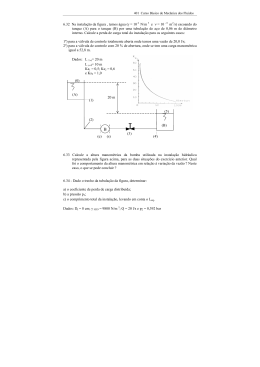
Dimensionamento das tubulações e perda de carga.
Número de Reynolds
Re =
v ⋅ dt
ν
v em cm / s; d t em cm; ν é a vis cos idade em Stokes
Em sistemas óleo-hidráulicos recomenda-se que o fluido escoe laminarmente
para reduzir a perda de carga e o aquecimento nas tubulações. Recomenda-se
também:
•Comprimento da tubulação L < 12 m
•Vazões entre 20 e 200 litros por minuto
•Variações moderadas de temperatura
pode-se também utilizar:
⎛ 1 ⎞
⎜⎜
⎟⎟
3
,
3
⎝
⎠
v = 121,65⋅ P
v em cm/ s; P em bar
Da continuidade estabelecemos o diâmetro interno mínimo.
dt =
Q
d t em cm; Q em l / min; v em cm / s
0,015 ⋅ π ⋅ v
Deve-se adotar o 1º diâmetro comercial acima do calculado (tabela 4.3)
Exemplo: Dimensionar as tubulações de sucção, pressão e retorno de um
sistema hidráulico que terá uma vazão máxima de 60 litros por minuto e
pressão de 120 bar. Adote a viscosidade do óleo como sendo ν= 0,45 St.
Na sucção :
dt =
Q
60
=
= 3,57 cm
0,015 ⋅ π ⋅100
0,015 ⋅ π ⋅ v
ν
da tabela d com = 3,80 cm d ext = 4,2 cm
Verificação do escoamento
vd 100 ⋅ 3,8
Re =
=
= 844,4 la min ar OK
0,45
ν
Na tubulação de pressão :
v = 121,65 ⋅ p
dt =
⎛ 1 ⎞
⎜⎜
⎟⎟
⎝ 3, 3 ⎠
= 121,65 ⋅120
Q
=
0,015 ⋅ π ⋅ v
⎛ 1 ⎞
⎜⎜
⎟⎟
⎝ 3, 3 ⎠
= 519 cm / s
60
= 1,57 cm
0,015 ⋅ π ⋅ 519
da tabela d com = 1,60 cm d ext = 1,90 cm = 3 / 4"
Verificação do escoamento
vd 519 ⋅1,6
Re =
=
= 1845,3 la min ar OK
ν
0,45
Na tubulação de retorno :
dt =
Q
=
0,015 ⋅ π ⋅ v
60
= 2,06 cm
0,015 ⋅ π ⋅ 300
da tabela d com = 2,10 cm d ext = 2,50 cm
Verificação do escoamento
vd 300 ⋅ 2,10
Re =
=
= 1400 la min ar OK
ν
0,45
Perda de Carga
ΔPT = ΔP + dP
dP = perda de c arg a nas válvulas da linha de pressão ( tabelado)
ΔP = perda de c arg a na tubulação (distribuída + localizada)
Deve − se também satisfazer a segu int e condição :
PN = Ptb + ΔPT
PN = pressão no min al
Ptb = pressão de trabalho
Perda de c arg a na tubulação
ΔP =
ψ ⋅ 5 ⋅ LT ⋅ ρ ⋅ v 2
d t ⋅10
10
(bar )
⎧ 64
⎫
tan
tubo
rígido
e
temperatur
a
cons
te
⎪ Re
⎪
⎪
⎪
75
⎪
⎪
ψ = fator de atrito ⎨ tubo rígido e temperatura var iável ⎬
⎪ Re
⎪
⎪ 90
⎪
var
tubo
flexível
e
temperatur
a
iável
⎪ Re
⎪
⎩
⎭
LT = comprimento real + comprimento equivalente em cm
ρ = massa específica do fluido = 881,1 kg / m 3 para óleo SAE 10
v = velocidade do escoamento em cm / s
d t = diâmetro int erno cm
5
fator de conversão
10
10
Perda Térmica
q (kcal / h ) = 1,434 ⋅ ΔPT (bar ) ⋅ Q B (l / min)
Exemplo: Determinar a perda de carga total e a perda térmica de um circuito que
contém as seguintes características:
1 válvula de controle direcional tipo J
1 válvula de seqüência tipo DZ10P (AÆB)
1 válvula controladora de fluxo tipo DRV8 (posição 5)
L=5m
dext = 5/8”
1 te de saída bilateral
2 tes de passagem direta
2 curvas de 90º raio longo
2 cotovelos 90º raio médio
Q = 45 l/min
PN = 150 bar
Ptb = 60 bar
Tubos rígidos de temperatura variável