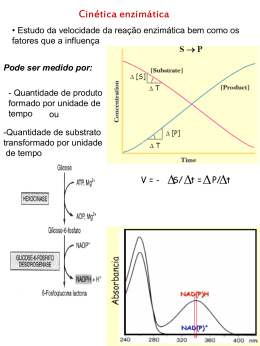
1
Degustação de trechos de livros sugeridos
Enzimas
Fonte: Wilson & Walker. Principles and Techniques of Biochemistry and Molecular
Biology, 7ed. Página 581Quando uma enzima é misturada com um excesso de substrato há um período de tempo
inicial curto (algumas centenas de microsegundos) em que os intermediários levando a
formação do produto aumentam gradativamente (Figura 15.1 pág 585 do livro). Esta
etapa chamada de estado pré-estacionário requer técnicas especiais para o estudo os
quais serão discutidos na Seção 15.3.3. Após o estado pré-estacionário, a velocidade da
reação e a concentração dos intermediários alteram-se relativamente de forma lenta com
o tempo constituindo a chamada cinética do estado estacionário. Medidas do progresso
da reação durante esta fase resultam na relação mostrada na Figura 15.2. As tangentes
desenhadas a partir da origem das curvas de concentração de substrato (S) e de produto
(P) versus o tempo permitem calcular a velocidade inicial (o). Esta é a velocidade
máxima para uma determinada concentração de enzima e substrato sob as condições
experimentais definidas. Medidas da velocidade inicial de uma reação catalisada
enzimaticamente são essenciais para o completo entendimento do mecanismo de ação
da enzima, bem como para a estimativa da atividade de uma enzima em uma amostra
biológica. Seu valor numérico é influenciado por vários fatores, incluindo concentração
de substrato e enzima, pH, temperatura e a presença de ativadores ou inibidores.
Para várias enzimas, a velocidade inicial, o, varia hiperbolicamente com a
concentração do substrato para uma concentração fixa de enzima (Figura 15.3). A
equação matemática que expressa essa relação hiperbólica entre velocidade inicial e a
concentração de substrato é conhecida como equação de Michaelis-Menten:
o = Vmax[S]
Km + [S]
Onde Vmax é o valor máximo da velocidade inicial quando todos os sítios ativos estão
ocupados, Km é a constante de Michaelis e [S] é a concentração do substrato. Em baixas
concentrações do substrato a ocupação dos sítios ativos das enzimas é baixa e a
velocidade da reação é diretamente relacionada ao número de sítios ocupados. Isto é,
próxima da cinética de primeira-ordem em que a velocidade é proporcional à
concentração do substrato. Em concentrações altas do substrato, todos os sítios ativos
são ocupados e a reação torna-se independente da concentração do substrato, pois não
há como formar mais complexos enzima-substrato (ES), observando-se assim uma
cinética de ordem-zero ou de saturação em relação ao substrato. Sob estas condições a
velocidade da reação é somente dependente da conversão do complexo enzimasubstrato, ES, em produto (P) e da difusão dos produtos a partir da enzima.
Pode ser observado a partir da equação 15.1 que quando o =0.5 Vmax, Km=[S]. Então,
Km é numericamente igual à concentração do substrato quando a velocidade inicial é
igual à metade da sua velocidade máxima (Figura 15.3) tendo como unidade a
molaridade. Valores de Km estão na faixa de 10-2 a 10-5 M e são importantes pois
permitem calcular a concentração do substrato necessária para saturar todos os sítios
ativos da enzima. Quando a [S]>>Km, a equação 15.1 é reduzida a o Vmax, mas um
simples cálculo revela que quando [S] = 10 Vmax, o é somente 90% Vmax e que quando
1
2
[S] = 100 Km, o =99 % Vmax. Apreciações deste tipo são importantes para os ensaios
enzimáticos.
Como mencionado anteriormente, reações catalisadas enzimaticamente ocorrem por
meio da formação de um complexo enzima-substrato em que o substrato (S) liga-se nãocovalentemente ao sítio ativo da enzima (E). A formação deste complexo para a maioria
das enzimas é rápido e reversível e é caracterizado por uma constante de dissociação, Ks
do complexo:
Onde k1 e k-1 são as constantes de velocidade para as reações de formação e dissociação
do complexo ES, respectivamente. No equilíbrio, as velocidades de formação e
dissociação são iguais e a lei de ação das massas pode ser aplicada para a reação
reversível:
k1[E][S] = k-1[ES]
Portanto,
Ks = [E][S] = k-1 = 1
[ES]
k1 Ka
Onde Ka é a constante de associação (ou afinidade).
Pode ser observado que quando o Ks é numericamente grande, o equilíbrio está a favor
das formas E e S livres. Por outro lado, quando o Ks é numericamente pequeno, o
equilíbrio está a favor da formação do complexo ES. Portanto, Ks é inversamente
proporcional à afinidade da enzima pelo substrato.
A conversão de ES em produto (P) pode ser representada pela equação:
Onde k2 é uma constante de primeira ordem para a reação.
Em alguns casos a conversão de ES em E e P pode envolver vários estágios e pode não
ser essencialmente irreversível. A constante de velocidade k2 é geralmente menor que
k1 e k-1, e em alguns casos muito menor. Em geral, portanto, a conversão e ES em
produtos é a etapa limitante tal que a concentração de ES é essencialmente constante,
mas não necessariamente a concentração de equilíbrio. Nestas condições a constante de
Michaelis, Km, é dada por:
Km = k2 + k-1 = Ks + k2
k1
k1
É evidente, que nestas circunstâncias, Km deve ser numericamente maior que Ks e
somente quando k2 é muito pequeno o Km se aproxima do valor de Ks. A relação entre
2
3
estas duas constantes torna-se mais complicada pelo fato de que para algumas reações
enzimáticas dois produtos (P1 e P2) são gerados sequencialmente, cada um deles
controlado por constantes de velocidade diferentes. Portanto, cuidados devem ser
tomados na interpretação do significado de Km em relação ao Ks. A relação matemática
entre Km e Ks e Km e afinidade da enzima pelo substrato só pode ser apreciada
totalmente somente quando o mecanismo completo da reação é conhecido.
Embora a equação de Michaelis e Mentem possa ser usada para o cálculo de Vmax e Km,
seu uso é sujeito a dificuldades na determinação experimental de o em altas
concentrações de substrato, em outras palavras, na extrapolação da curva hiperbólica
para obtenção de um valor exato de Vmax. Transformações lineares da equação de
Michaelis e Mentem são alternativas comumente utilizadas. O mais popular destes é a
equação de Lineweaver-Burk obtida tomando-se o recíproco da equação de Michaelis
e Mentem.
1 = Km  1 + 1
o
Vmax [S] Vmax
O gráfico de 1/o (y) versus 1/[S] (x) resulta em uma reta, onde a inclinação é Km/Vmax,
o intercepto no eixo 1/o é igual a 1/Vmax e o intercepto no eixo 1/[S] é igual a -1/Km.
Gráficos alternativos são baseados na equação de Hanes e na de Eadie-Hofstee.
Também existem softwares de regressão não linear como o DynaFit (www.biokin.com)
e BRENDA (www.brenda-enzymes.info), os quais são utilizados preferencialmente em
casos onde se requer dados precisos de cinética.
É importante notar que enquanto o Km é uma característica da enzima e de seu substrato
e o seu valor independente da quantidade da enzima utilizada para a sua determinação
experimental, o mesmo não é verdade para o Vmax. Não existe um valor absoluto de Vmax
e o seu valor depende da quantidade de enzima usada. Essa característica é ilustrada na
Figura 15.3 (página 586) e é adicionalmente discutida no Exemplo 1 (página 589).
Além de Km e Vmax, uma outra constante catalítica de importância é kcat, ou número de
renovação (turnover number), definido como:
kcat = Vmax
[Et]
Onde [Et] é a concentração total de enzima. O número de renovação é o número
máximo de mols de substrato que podem ser convertidos em produto por mol de enzima
em uma unidade de tempo. Sua unidade é dada pelo recíproco do tempo em segundos (s1
). Seus valores variam de 1 a 107 s-1. Catalase possui um número de renovação de 4 
107 s-1 e é uma das enzimas mais eficientes conhecidas. O potencial catalítico de um alto
valor de número de renovação só pode ser atingido em altas concentrações de substrato
(concentrações saturantes) e isso é raramente atingida em condições celulares. Uma
constante alternativa, chamada de constante de especificidade, definida como kcat/Km, é
uma medida de quão eficientemente uma enzima converte substrato em produto em
baixas concentrações de substrato. Sua unidade é dada por M-1s-1.
Para um substrato ser convertido em produto, moléculas de substrato e da enzima
precisam primeiramente colidir por difusão randômica e então combinar-se e uma
orientação correta. Difusão e colisão possuem constantes de velocidades teóricas
3
4
limitantes em torno de 109 M-1s-1 e várias enzimas, incluindo acetilcolina esterase,
anidrase carbônica, catalase, -lactamase e triosefosfato isomerase, possuem constantes
de especificidade próximas deste valor indicando que elas estão próximas ao máximo de
eficiência catalítica. Como a constante de especificidade é uma razão entre duas outras
constantes, enzimas com constantes de especificidade similares possuem valores
bastante diferentes de Km. Como exemplo, catalase possui constante de especificidade
de 4  107 M-1s-1 com um Km de 1.1 M (bastante alto), por outro lado, fumerase possui
uma constante de especificidade de 3.6  107 M-1s-1com um Km de 2.5  10-5 M (bem
baixo). Complexos multienzimáticos conseguem superar limitações decorrentes de
difusão e colisão. Neste caso, o produto de uma reação é passada diretamente por um
processo de direcionamento (channelling) para o sítio ativo da próxima enzima na via
como consequência da justaposição no complexo, portanto eliminando limitações
referentes à difusão.
Efeito da concentração do substrato
Pode ser observado para reações enzimáticas monosubstrato que eles obedecem a
cinética de Michaelis e Mentem:
o = k2[E][S]
Km + [S]
E, portanto,
o = k2 [E]
(Km/[S]) + 1
Então, quando a concentração do substrato é grande, a equação anterior reduz-se a
o = k2 [E]
Onde a velocidade é proporcional à concentração do susbstrato. Esta é a base para
determinação experimental da atividade enzimática de uma amostra biológica.
4
5
Inibição de reações enzimáticas
- Inibição reversível competitiva
Inibidores reversíveis combinam-se não covalentemente com as enzimas e, portanto
podem ser removidas facilmente por diálise. Inibidores reversíveis competitivos
combinam-se no mesmo sítio que o substrato e deve ser, portanto ser relacionado
estruturalmente com o substrato. Como exemplo pode-se citar a inibição da succinato
desidrogenase por malonato:
CH2COOH

CH2COOH
CH2COOH

COOH
Ácido succínico (Substrato)
Ácido malônico (Inibidor)
 Succinato desidrogenase
 Succinato desidrogenase
CHCOOH

CHCOOH
Nenhuma reação
Ácido fumárico (Produto)
Todos os inibidores reversíveis são caracterizados por uma constante de dissociação, Ki,
chamada de constante de inibição, que pode estar relacionada com a constante de
dissociação de EI (KEI) ou de ESI (KESI). Para inibidores competitivos as duas equações
seguintes pode ser escritas como:
E+S
ES
E+P
E+I
EI
sem reação
Como a ligação do substrato e do inibidor ocorrem no mesmo sítio, o efeito do inibidor
pode ser desfeito aumentando-se a concentração do substrato. O resultado é que o Vmax
não se altera, mas a concentração necessária para atingir o Vmax é aumentada de forma
que quando o = 0.5 Vmax:
[S] = Km 1 + [I]
Ki
Onde a [I] é a concentração do inibidor.
Pode ser observado pela equação acima que Ki é igual à concentração do inibidor que
aparentemente dobra o valor de Km. Com este tipo de inibidor, Ki é igual a KEI, enquanto
KESI é infinito pois ESI não é formado. Na presença de inibidor competitivo, a equação
de Lineaweaver-Burk torna-se:
1
0
=
Km
Vmax

1
[S]
1+
[I]
Ki
+
1
Vmax
Aplicação desta equação permite o diagnóstico de inibição competitiva (Figura 15.5a,
página 593). O valor numérico de Ki pode ser calculado a partir do gráfico de
Lineaweaver-Burk para a reação sem o inibidor e com o inibidor. Na prática, no
5
6
entanto, valore mais preciso é obtido através de um segundo gráfico (Figura 15.6,
página 593). A reação é conduzida para várias concentrações do substrato na presença
de algumas concentrações de inibidor, e em seguida constrói-se um gráfico de
Lineawever-Burk para cada concentração do inibidor. Um segundo gráfico é construído
plotando-se os diferentes valores de inclinação ou de Km aparente [Km’, que é igual a Km
(1+ [I]/Ki) e que pode ser determinado através do intercepto no eixo 1/[S] ] versus
concentração do inibidor. Em ambos os gráficos o intercepto no eixo de [I] dá o valor de
–Ki.
-Inibidor reversível não-competitivo
Um inibidor reversível não-competitivo combina-se com a enzima em um sítio diferente
do sítio ativo do substrato. Por mais que o substrato ainda possa se ligar ao complexo EI
formando um complexo ternário ESI, este complexo não é capaz de converter substrato
em produto e é chamado de complexo final “suicida”. Como a inibição envolve um
sítio distinto do sítio catalítico, a inibição não pode ser revertida pelo aumento da
concentração do substrato. A consequência é que Vmax e não o Km é reduzido, pois o
inibidor não afeta a ligação do substrato à enzima, mas afeta a quantidade de ES que
pode prosseguir em direção à formação do produto. Neste tipo de inibição KEI e KESI são
idênticos e Ki é numericamente igual a ambos. Neste caso a equação de LineaweaverBurk torna-se:
1
0
=
Km
Vmax

1
[S]
+
1
Vmax
1+
[I]
Ki
Uma vez que inibidores não-competitivos tenham sido diagnosticados, o valor de Ki é
melhor determinado através de um segundo gráfico obtido plotando-se os diferentes
valores de inclinação ou de 1/Vmax’ (intercepto no eixo 1/o) versus concentração de
inibidor ([I]). Em ambos os gráficos o intercepto no eixo de [I] dá o valor de –Ki.
- Inibidor reversível acompetitivo
Um inibidor reversível acompetitivo pode-se ligar somente ao complexo ES e não à
enzima livre e, portanto o inibidor se liga a um sitio que é criado durante a alteração
conformacional da enzima promovida pela ligação ao substrato. O complexo ternário,
ESI, resultante é chamado de complexo final “suicida”.
Assim como com o inibidor não-competitivo, o efeito do inibidor não pode ser revertido
pelo aumento da concentração do substrato, mas neste caso ambos Km e Vmax são
reduzidos por um fator de (1+ [I]/Ki). Uma concentração de inibidor igual ao Ki,
portanto irá diminuir o valor de Km e Vmax pela metade. Com este tipo de inibidor, KEI é
infinito, pois o inibidor não pode se ligar à enzima livre e, portanto Ki é igual a KESI.
Neste caso a equação de Lineaweaver-Burk torna-se:
1
Km
1
1
[I]
1+
=

+
Vmax [S]
Vmax
Ki
0
O valor de Ki é mais precisamente determinado a partir de um segundo gráfico de
1/Vmax’ ou I/Km’ versus a concentração do inibidor. Em ambos os gráficos o intercepto
no eixo de [I] dá o valor de –Ki.
6
7
- Inibidor reversível misto
Para alguns inibidores o complexo ESI possui alguma atividade catalítica ou o KEI e
KESI não são iguais e nem infinitos. Nestes casos são obtidas cinéticas de inibição do
tipo misto. Na inibição mista as retas obtidas nas reações sem inibidor e com inibidor
sofrem intersecção acima ou abaixo do eixo 1/[S]. O valor de Ki pode ser determinado
através de um segundo gráfico de inclinação ou de 1/Vmax’ versus a concentração do
inibidor. Em ambos os gráficos o intercepto no eixo de [I] dá o valor de –Ki. A inibição
não-competitiva pode ser classificada como um tipo especial de inibição mista.
Inibição irreversível
Inibidores irreversíveis, tais como compostos organofosforados e organomercúricos,
cianeto, monóxido de carbono, sulfito de hidrogênio, combinam com enzima para
formar ligação covalente estável. A extensão da inibição de uma enzima é dependente
da constante de velocidade (e, portanto do tempo) para a formação da ligação covalente
e também da concentração do inibidor presente. O efeito de inibidores irreversíveis, que
não podem ser removidos por técnicas físicas como a diálise, é reduzir a quantidade de
enzima disponível para a reação. A inibição envolve reações com grupos funcionais,
como hidroxilas e sulfidrilas, ou com átomos de metais no sítio ativo ou alostérico.
Assim, compostos organofosforados, diisopropil-fofofluoridato, reage com a serina do
sítio ativo de esterases tais como a acetilcolinesterase, enquanto compostos
organomercúricos como o p-hidroximeriobenzoato reage com cisteínas, em ambos os
casos resultando na formação de ligações covalentes e inibição enzimática. Tais
inibidores são valiosos n estudo de sítio ativo de enzimas.
Aplicações da inibição enzimática
O estudo da classificação e dos mecanismos de inibição enzimática é de importância em
diversos aspectos:
- fornece informações sobre o mecanismo pelo qual a enzima promove a atividade
catalítica (mais detalhes na seção 15.4.1 página 611);
- fornece informações de possíveis mecanismos de regulação de atividades metabólicas
in vivo;
-permite a síntese de inibidores específicos para serem utilizadas como agentes
terapêuticos bloqueando vias metabólicas chaves envolvidas em condições clínicas
(mais detalhes na seção 18.1.2, página 709).
Link para as figuras
http://www.cambridge.org/gb/knowledge/isbn/resources/item2713153/?site_locale=en_GB#
Chapter 15
GR01: Fig.15.1 Figura do estado pré-estacionário
GR02: Fig.15.2 Cálculo de o
GR03: Fig.15.3 Efeito da [S] na o e efeito de diferenes concentrações de inibidores
GR04: Fig.15.4 Gráficos Lineaweaver-Burk, Hanes e Eadie-Hofstee
GR05: Fig.15.5 Gráficos Lineaweaver-Burk mostrando o efeito de 3 tipos de inibidores (a)
GR06: Fig.15.6 Gráfico Lineawever-Burk (a) e Gráfico para determinação de Ki determination (b)
7