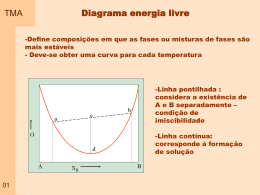
TMA
Capacidade calorífica – Volume constante
Considerando uma condição em
que não é realizado trabalho
U  q v
dU  dq v
q  CT
01
CALORIMETRIA
bomba calorimétrica
TMA
Capacidade calorífica – Volume constante
Diagrama da variação da energia
interna em função da temperatura
a volume constante
O coeficiente angular da curva, em
cada temperatura é a capacidade
calorífica a volume constante
 U 
Cv  

 T  v
02
TMA
Entalpia
H  U  pV
U, P, V são funções de estado. Assim H também é;
Esta associado ao calor envolvido em um processo realizado
a pressão constante
03
TMA
Capacidade calorífica – Pressão constante
 H 
Cp  

 T  p
A capacidade calorífica tem sua
variação
em
função
da
temperatura pode ser considerada
como constante para gases ideais
Para sistemas não ideais pode ser
representada matematicamente
Cp 
C p,m
5
3
R Cv  R
2
2
c
 a  bT  2
T
Relação entre Cv e Cp
04
Cp  Cv  nR
DSC - Calorímetro diferencial de varredura – Calorimetria diferencial exploratória
TMA
Expansão adiabática
em expansão adiabática q=0
05
TMA
Calor específico
Temos as duas relações conhecidas:
 U 
Cv  

 T  v
 H 
Cp  

 T  p
Tentativas de determinar os valores de Cv e Cp
1819 (Dulong e Petit) – definiram que capacidade calorífica
molar de todos os elementos sólidos é igual a 3R
Cv  3R  24,9
06
TMA
Resultados experimentais (1947)
Cv(Joules/K)
25
Pb
20
Cu
15
Si
10
5
0
Diamante
0
50
100
150
200
Temperatura (K)
250
300
Einstein – Física quântica – arranjo cristalino de n átomos –
considerou que cada átomo apresenta oscilação harmônica
independente de sua posição na rede cristalina
Temperatura característica de Einstein
07
h
E 

Onde:  é a freqüência de vibração atômica
TMA
Einstein
X
experimental
25
Cv (Joules/K.mol)
20
Einstein
15
Al D= 385 K
10
5
0
0
0,2
0,4
0,6
0,8
1,0
T/
Se T/ aumenta – Cv tende a 3R
Se T tende a zero Cv tende a zero
08
1,2
1,4
1,6
1,8
2,0
Debye
TMA
Debye – considerou que a freqüência vibracional não era a
mesma para todos os átomos.  - está entre a distância
interatômica e 2x a distância interatômica
25
Cv (Joules/K.mol)
20
Einstein
15
Al D= 385 K
10
5
0
0
09
0,2
0,4
0,6
0,8
1,0
T/
1,2
1,4
1,6
1,8
2,0
Temperatura de Debye
TMA
Cv ( Joules/K.mol)
30
25
Substância
Pb
K
Na
Sn
Cd
Au
Ag
Pt
Zn
Cu
Mo
Al
Fe
C(dia.)
10
D temperatura
altas
90 K
99
159
160
160
180
213
225
235
315
379
389
420
1890
baixas
20
15
205
321
379
385
428
2230
O
10
O
Ag
D=213
O
O
O
O
O
O
O
O
O
O
O O
O O
O
O
O
O
O
O
O
O
O
Al
D=389
O
O
5
O
O
O
O
O
O
O
O
O
0
1,0
127 K
129
162
Pb
D=90,3
O
O
2,0
Log T
Oa
O
O O
O
O
C(diamante)
D=1890
3,0
TMA
Outras considerações
Efeito da temperatura sobre a energia interna e o movimento
atômico.
Cv  24,93  bT
Relação empírica Cp - T
Cp  a  bT  cT2
A equação tem validade para intervalos de temperatura
definidos
Para metais líquidos, em geral Cp = constante
11
Cp – Valores Tabelados
TMA
Elemento
Al (Sólido)
Al (líquido)
Au (Sólido)
Au (líquido)
Cu (Sólido)
Cu (líquido)
Fe ()
Fe ()
Fe ()
Fe ()
Fe (líquido)
C (diamante)
C (grafite)
O2 (gás)
12
Cp(joules/K.mol)
20,7 +12,4 10-3 T
29,8
23,7 +5,19 10-3 T
29,3
22,6 +6,28 10-3 T
31,4
17,5 +24,8 10-3 T
38
7,7 +19,5 10-3 T
43,9
41,8
9,12 +13,2 10-3 T-6,19 105 T-2
17,2 +4,27 10-3 T-8,79 105 T-2
30,0 +4,18 10-3 T-1,7 105 T-2
Intervalo de T
298 -Tm
Tm - 1273
298 -Tm
Tm - 1600
298 -Tm
Tm - 1600
298 -1033
1033-1181
1181-1674
1674 -Tm
Tm- 1873
298 - 1200
298 - 2300
298 - 3000
TMA
Cp – Curvas características de materiais
45
Fe()
40
Fe()
Fe()
Fe()
Cp Joule/K.mol
35
30
O2(g)
Cu(s)
Al(s)
25
Cu(l)
Au(l)
Al(l)
Au(s)
C(diamante)
20
C(grafite)
15
10
5
0
400
600
800
1000
1200
Temperatura (K)
13
1400
1600
1800
Exercício
TMA
1)
10 litros de gás ideal monoatômico, mantido a 25 ºC e 10 atm é
expandido até atingir a pressão final de 1 atm. A capacidade
calorífica molar do gás a volume constante (Cv) é 3/2 R e é
independente da temperatura.
Calcular o trabalho realizado, o calor absorvido e as mudanças de
energia interna e entalpia para o gás se o processo ocorre:
isotermicamente e reversivelmente
adiabaticamente e reversivelmente
14
Termoquímica
TMA
(ATKINS) – Termoquímica é a investigação do calor produzido
ou consumido nas reações químicas. Trabalha com os
conceitos de determinação do calor envolvido em processo a
pressão ou volume constante e conseqüentemente com U e
H correspondendo ao calor de reação.
dH  q p  nCp dT
dU  qv  nCv dT
Transformação Física
H2O(l)  H2O(g)
vapH(273)  6,01 kJ / mol
Reação química
15
9
C3H 6 (g)  O 2 (g)  3CO 2 (g)  3H 2 O
2
 r H  - 2058kJ/mol
TMA
Termoquímica
Reagentes
Produtos
Estado padrão – O estado padrão de uma substância, numa
certa temperatura, é o da substância pura sob pressão de 1
bar.
Variação de entalpia padrão – A variação de entalpia de
reação ou processo físico é a diferença entre as entalpias dos
produtos nos respectivos estados padrões e a entalpia dos
reagentes, também nos respectivos estados padrões.
Pode ser referida a qualquer temperatura.
Assumiu-se como temperatura de referência 298,15 K.
16
TMA
Entalpia de reação
Variação de entalpia padrão
(a) Entalpia de transformações físicas – variação de entalpia
associada a uma mudança de estado físico ( entalpia
padrão de transição)
H2O(s)  H2O(l )
0
 fus H273
 6,01 kJ / mol
CONCEITO DE FUNÇÃO DE ESTADO
H2O(s)  H2O(l)
fus H
H2O(l)  H2O(g)
vapH
H2O(s)  H2O(g)
17
sub H  fus H  vapH
TMA
18
Conceito de função de estado
TMA
Entalpia de reação
(b) Entalpia de transformação química – A entalpia padrão de
reação é a variação de entalpia associada a
transformação de reagente no estado padrão em produtos
também no estado padrão
Reagente isolado no
estado padrão
Produtos isolados, puros,
nos
respectivos
estados
padrões
H 2 ( g )  O2 ( g )  H 2O( g )
0
r H298
 - 241,82kJ/mol
Efeito da quantidade de reagentes e produtos
2A  B  3C  D
r H 
 H
Pr odutos
m

 H
m
Re agentes
r H  3Hm (C)  Hm (D)  2Hm (A)  Hm (B)
19
Onde Hm(c)é a entalpia padrão molar da espécie C na
temperatura constante
TMA
Entalpia de reação
Reações exotérmicas
C  O2   CO2 
H0298  -393510J
Reação endotérmica
ZnO  C  CO  Zn
0
H1373
 349000J
Calor de formação : é a variação de entalpia que acompanha
a formação de um mol de um composto, a partir de seus
elementos constituintes, na sua forma mais estável ã
temperatura de referência ( no caso 298 K ) e sob
pressão de 1 atm.
2 Al 1,5O2   Al2O3
20
H0298  1674000J
Assume que a reação é completa
TMA
Entalpia de reação
Calor de reação: é a variação da entalpia que acompanha a
reação , quando as quantidades de reagentes são
totalmente consumidas, de acordo com a equação química
balanceada, na temperatura considerada.
3 Fe2O3  CO  2 Fe3O4  CO2 
0
H1000
 46700J
O calor de reação a 1000K é igual a 46700 J. Este
é o calor absorvido, sob pressão constante de 1
atm, quando 3 moles de hematita são reduzidos
por um mol de monóxido de carbono, para formar
dois moles de magnetita e um mol de dióxido de
carbono. Supondo-se a reação completa.
21
TMA
Entalpia de reação
(C) A lei de Hess – é possível combinar as entalpias padrões
de várias reações para se ter a entalpia de outra reação
A entalpia padrão
de uma reação é igual a soma das
entalpias padrões de reações parciais em que a reação
possa ser dividida.
9
0
C3 H 6 ( g )  O2 ( g )  3CO2 ( g )  3H 2 O
 r H 298
?
2
0
C3 H6 ( g )  H 2 ( g )  C3 H8 ( g )
r H 298
 -124kJ/mol
C3 H8 ( g )  5O2 ( g )  3CO2 ( g )  4H2O(l )
1
H 2O(l )  H 2O( g )  O 2
2
9
C3 H 6 ( g )  O2 ( g )  3CO2 ( g )  3H 2 O
2
22
0
r H298
 - 2220kJ/mol
0
 r H 298
  286 kJ/mol
0
 r H 298
 - 2058kJ/mol
TMA
Conceito de função de estado
(e) Entalpia de reação em função da entalpia de formação
2HN3 (l)  2NO(g) H2O2 (l)  4N2 (g)
 r H   f H(H 2O2 , l)  4 f H( N 2 , g)
 2 f H( NH3 , l)  2 f H( NO, g)
 r H 0  187 ,78  2(0)
 2(264 ,0  2(90,25)
r H 0  892,3kJ / mol
23
TMA
(e) Calor de combustão e poder calorífico
Quando um mol de uma substancia é completamente
queimado com oxigênio, há liberação de calor; H<0
Exemplo:
C  O2   CO2 
C2 H6O  3O2  2CO2  3H2O
24
H0298  94051cal
H0298  Calor de combustao
TMA
Entalpia e temperatura
(f) Entalpia de reação e temperatura – A entalpia de reação
em temperatura diferente da temperatura ambiente pode
ser estimada a partir da capacidade calorífica e da
entalpia de reação na temperatura ambiente. (ou outra
temperatura qualquer)
T2
H (T2 )  H (T1 )   C p dT
T1
25
TMA
Exemplo
1
Pb(s)  O 2 (g )  PbO (s)
2
H PbO(298)  219000 joule/ mol
CPb (s)  23,6  9,75x103 T joule / Kmol de 298K a Tm,Pb
CPb (l)  32,4  3,1x103 T joule / Kmol de Tm,Pb a 1200K
CPbO (s)  37,9  26,8x103 T joule / Kmol de 298K a Tm,Pb
CO(g)  30,0  4,18x103 T -1,7x105 T-2 joule / Kmol de 298K a 3000K
Hm,Pb  4810 joule / mol a 600K
Tm,Pb  600K
Tm,PbO  1159K
26
TMA
Exemplo
1
Pb(s)  O 2 (g )  PbO (s)
2
40
30
20
Entalpia H (kJ)
10
0
-170
-180
-190
-200
-210
-220
300
27
500
700
900
1100 300
Temperatura (K)
500
700
900
1100