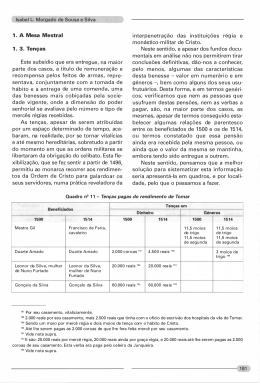
O BODE COMILÃO
r é o comprimento da corda então a extensão de pasto disponı́vel para o bode é igual à área da região
limitada pelos segmentos de recta [OM ] e [ON ] de comprimento r e pelo arco de circunferência M N . Esta área
2
é igual a um quarto da medida da área da circunferência de centro O e raio R, isto é, πR
4 .
1) Se
N
O
M
2
Como a medida da área do quadrado é igual a L2 , temos L2
=
πr 2
4 , pelo que
r=
2
π L.
R é o comprimento da corda então a extensão de pasto disponı́vel para o bode é igual à área da região
[ON ] de comprimento R e pelo arco de circunferência M N . Esta área
2
60
1
é igual a 360 = 6 da área da circunferência de centro O e raio R, isto é, πR
6 .
2) Se
limitada pelos segmentos de recta [OM ] e
N
O
M
Como metade da área do triângulo é igual a hL
4 (onde h denora a altura do triângulo) e atendendo ao Teorema
de Pitágoras, h
=
L2 −
L 2
2
=
√
3L
2 , teremos
πR2
6
√
√ 2
3L
L 3 3
=
=⇒ R =
.
8
2
π