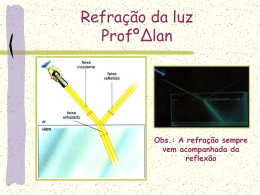
Refração da luz
Professor. PENHA
Obs.: A refração sempre
vem acompanhada da
reflexão
Refração da luz
A velocidade da onda luminosa depende da
densidade do meio. Quanto maior a
densidade de um meio, menor a velocidade
de propagação da onda nesse meio.
Refração da luz
Refringência: resistência
oferece a passagem da luz.
que
o
meio
 maior densidade

meio mais refringent e ( )   menor velocidade
 menor compriment o de onda

 menor densidade

meio menos refringent e ()   maior velocidade
 maior compriment o de onda

Refração da luz - Representação
Luz passando do meio menos para o meio mais refringente:
Raio
incidente
Normal
i
I
R
r
Raio
refratado
V V
R
I


   λR  λI

ˆ ( se iˆ  0)
ˆ
r

i


Neste caso podemos dizer que o raio refratado
aproxima-se da normal
Refração da luz - Representação
Luz passando do meio mais para o meio menos refringente:
Raio
incidente
Normal
i
I
R
r
V V
R
I


   λR  λI

ˆ
ˆ

rˆ  i ( se i  0)
Raio
refratado
Neste caso podemos dizer que o raio refratado
afasta-se da normal
Refração da luz - Representação
Luz passando do meio mais para o meio menos refringente:
Normal
i=0º
Raio
incidente
I
R
r=0º
Raio
refratado
V V
R
I


   λR  λI

ˆ 0o
ˆ
r

i


Neste caso tivemos uma refração sem desvio
Refração da Luz
Desvio angular do raio refratado
Normal
Normal
i
i
r

  rˆ  iˆ
r

  iˆ  rˆ
Índice de Refração absoluto de um meio
Definição: é a razão entre a velocidade da luz no
vácuo e a velocidade da luz no meio considerado.
Nmeio
Vvácuo

Vmeio
onde Vvácuo  3  108 m s
O índice de refração depende da densidade do
meio, do material e da freqüência utilizada para
medi-lo.
Índice de Refração - Observações
Nmeio
Vvácuo

Vmeio
onde Vvácuo  3  108 m s
Nvácuo  1

 Nar  1
N
 demais meios  1
Índice de refração relativo
O índice de refração do meio R em relação ao meio
I, é definido por:
NR ,I
Vvácuo
NR
VR
VI



NI Vvácuo VR
VI
Leis da Refração
O raio refratado, o
raio incidente e a
normal são coplanares.
Lei de Snell:
I NR
sen iˆ VI



R NI
sen rˆ VR
VI= velocidade da onda incidente
VR=
velocidade
refratada
da
onda
I= comprimento de onda da
onda incidente
R= comprimento de onda da
onda refratada
NI= índice de refração do meio
de incidência
NR= índice de refração do meio
de refração
Ângulo Limite de Incidência
O ângulo de incidência é chamado de ângulo limite
(L) se o ângulo de refração for igual a 90o.
Raio
incidente
Normal
i= L
N
n
r= 90º
Raio
refratado
Refração rasante
n
ˆ
senL 
N
Reflexão Total da Luz
  
Condições para que ocorra reflexão total:  
i  L
N
N
N
n
r=0o
i=0o
N
i>L
Neste caso tivemos
uma reflexão total
i=L
i<L
Aplicação da reflexão total
Fibra Ótica
Funcionamento da Fibra Ótica
ar
i>L
casca
núcleo

casca
ar
Aplicação da reflexão total
Miragem
Aplicação da reflexão total
Miragem
I<L
I<L
I>L
Reflexão
total
Ar frio
Ar quente
Ar mais quente
Ar muito quente
Asfalto
DISPERSÃO DA LUZ
Vermelho
Alaranjado
Amarelo
Verde
Azul
Anil
Violeta
Dioptro Plano
É o conjunto de dois meios homogêneos e
transparente separados por uma superfície
plana.
Dioptro Plano
Dioptro Plano
observador
objeto
observador
objeto
Dioptro Plano
Altura Aparente dos Astros
A densidade do ar diminui com a altura
Altura aparente dos astros
A densidade do ar diminui com a altura. Observe
esquema a seguir:
Imagem
Objeto
Lâmina de faces paralelas
É uma associação de dois dioptros planos
Lâmina de faces paralelas
RAIO
INCIDENTE
N
i
AR
A
VIDRO
r
espessura
r
AR
desvio
C
i
N
RAIO
EMERGENTE
LENTES ESFÉRICAS
-Classificação
- Seus elementos
- Formação da Imagem
Definição A: Associação de dois dioptros, na
qual um deles é necessariamente esférico,
enquanto o outro pode ser plano ou esférico.
(Ex.)
Dioptro
Dioptro
esférico
plano
C1 e C2 - centros de curvatura das faces da lente;
R - raios de curvatura das faces da lente;
V1 e V2 - vértices das faces;
e - espessura da lente;
O - centro óptico da lente;
E.P. - eixo principal
Nomenclatura:
Se a espessura da lente diminui do centro
para a periferia, ela é dita de bordas
delgadas, exemplo abaixo;
Se a espessura, dela, aumenta do centro
para a sua periferia, então a denominamos,
lente de borda espessa.
Classificação das lentes
esféricas:
n(lente) > n(meio)
Observação:
• n(lente) > n(meio) teremos:
 lente de borda delgada convergente;
 lente de borda espessa divergente.
• n(lente) < n(meio) teremos:
 lente de borda delgada divergente;
 lente de borda espessa convergente.
Foco imagem de uma lente
(Fi)
Foco objeto de uma lente
(Fo)
Raios particulares ou notáveis
Construção da Imagem geometricamente.
(caso 1 - o objeto antes do ponto A –
imagem entre Fi e Ai)
(caso 2 - o objeto sobre o ponto A
– imagem sobre Ai)
(caso 3 - o objeto após o ponto A –
imagem atrás de Ai)
(caso 4 - o objeto sobre o ponto F –
imagem imprópria)
(caso 5 - o objeto entre F e O – imagem
atrás de Ao)
Lente divergente.
(caso 6 - o objeto em qualquer ponto –
imagem entre Fi e O)
OLHO HUMANO
FIM
OLHO HUMANO
FIM
OLHO HUMANO
FIM
OLHO HUMANO
FIM
OLHO HUMANO
FIM
OLHO HUMANO
FIM
OLHO HUMANO
FIM
OLHO HUMANO
FIM
GLOBO OCULAR
Esclerótica
Coróide
Retina
Humor aquoso
Cristalino
Córnea
Corpo vítreo
Nervo
óptico
Pupila
Íris
Músculo
ciliar
Ponto
cego
EMÉTROPE
VOLTA
MIOPIA
Longe
VOLTA
MIOPIA
VOLTA
MIOPIA
VOLTA
MIOPIA
VOLTA
EQUAÇÃO PARA ACOMODAÇÃO
DA IMAGEM PARA UM MIOPE
HIPERMETROPIA
Perto
VOLTA
HIPERMÉTROPE
VOLTA
HIPERMÉTROPE
VOLTA
HIPERMÉTROPE
VOLTA
EQUAÇÃO PARA ACOMODAÇÃO
DA IMAGEM PARA UM
HIPERMÉTROPE
ASTIGMATISMO
VOLTA
RESUMINDO
EMÉTROPE - NORMAL
MIOPIA - LONGE - DIVERGENTES
ASTIGMATISMO - CILÍNDRICAS
HIPERMET. E PRESB. - PERTO - CONVERG.
VOLTA