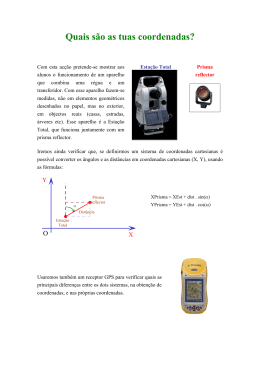
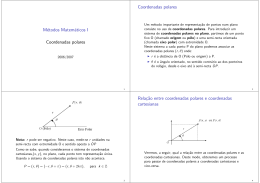
Números Complexos
Conceito Principal
Um número complexo é um número com esse formato
.
, onde a e b são números reais e
Utilizando o sistema de números reais, nós não tomamos a raiz quadrada de um número negativo, e
assim não deve ser um número real e, por conseguinte, é conhecido como a unidade imaginária.
Nós visualizamos um número complexo por duas dimensões gráficas que se chamam plano complexo.
Todo o número complexo possui duas partes: a parte real,
, que podem ser usadas como coordenadas cartesianas
plano complexo, em que
é ao longo do eixo horizontal e
, e uma parte imaginária,
para traçar z como um ponto no
ao longo do eixo vertical.
Alternando, pontos em um plano complexo também pode ser descritos usando coordenadas polares:
.
O argumento, , medindo (em radianos) o ângulo entre positivo Re(z) do eixo e a linha do segmento
conectado ao ponto z para a origem.
Fundamento Teórico
De acordo com o Teorema Fundamental da Álgebra, um polinômio de variável única n de
coeficientes reais diferente de zero deve ter exatamente n raízes, contando multiplicidade.
No entanto, em alguns casos, não é possível descrever todas as raízes utilizando números reais.
Por exemplo, o polinômio
deve ter duas raízes, uma vez que possui coeficientes reais e
grau 2, mas não são números reais que completam essa equação.
Assim, como fazer raízes não reais? Usamos os números complexos!
Defina I como
.
Dentro do sistema de números reais, não podemos tirar a raiz quadrada de um número negativo,
então não deve ser um número real e, portanto, é conhecido como a unidade imaginária.
Usando o conjunto de todos os números da forma
obter as duas raízes de
. (Quais são elas?)
, chamado número complexo, pode-se
O conjunto dos números reais, =, é o subconjunto do conjunto dos números complexos C, porque
cada número real tem a forma
.
Um número de forma
puramente imaginário para a parte real.
Conversão entre Coordenadas Cartesianas e Polares
Quando pontos complexos sobre o plano são descritos deve-se usar polar coordenadas:
, onde r é chamado de módulo ou magnitude de z e é chamado de argumento ou
fase de z.
Definimos o módulo como
, onde
Assim,
z.
.
O simbolo, , mede (em radianos) o ângulo entre o eixo positivo Re(z) eixo e a reta conectando
o ponto z a parte original.
Para converter um ponto do plano cartesiano na forma polar evice-versa, podemos usar a
fórmula de Euler;
.
Clique sobre o gráfico traçando um número complexo sobre um plano complexo.
Use os botões de radio para alternar entre o Coordenadas Cartesianas e a Cordenadas Polares.
Coordenadas Cartesianas
Coordenadas Polares