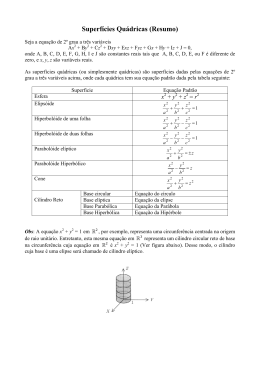
QUÁDRICAS QUÁDRICAS QUÁDRICAS ELIPSÓIDE ELIPSÓIDE ELIPSÓIDE EXEMPLO A figura 8.2.1-b mostra o elipsóide de revolução: O traço no plano xOz é a circunferência x 2 4 z 2 4 1, y 0 EXEMPLO Reduzir a equação à forma canônica, identificar e construir o gráfico da quádrica que ela representa 36 x 9 y 16 z 144 2 2 2 GRÁFICO 36xx+9yy+16zz=144 36xx+9yy+16zz=144 GRÁFICO EXEMPLO Reduzir a equação à forma canônica, identificar e construir o gráfico da quádrica que ela representa: 4x y 4z 2 2 2 16 GRÁFICO DE OUTRO ÂNGULO ELIPSÓIDE xx+yy+zz=4 ELIPSÓIDE ELIPSÓIDE a=b<c a=b>c x 2 a 2 x 2 a 2 y 2 a 2 y 2 a 2 z 2 c 2 1 z 2 c 2 1 ELIPSÓIDE ELIPSÓIDE ELIPSÓIDE HIPERBOLÓIDE DE UMA FOLHA Se na equação (4) dois dos coeficientes do 1º membro são positivos e um negativo, a equação representa um hiperbolóide de uma folha. HIPERBOLÓIDE DE UMA FOLHA HIPERBOLÓIDE DE UMA FOLHA HIPERBOLÓIDE DE UMA FOLHA HIPERBOLÓIDE DE UMA FOLHA HIPERBOLÓIDE DE UMA FOLHA EXEMPLO Reduzir a equação à forma canônica, identificar e construir o gráfico da quádrica que ela representa: 4x y 8z 2 2 2 16 4xx-yy+8zz=16 Exemplo EXEMPLO Reduzir a equação à forma canônica, identificar e construir o gráfico da quádrica que ela representa: 4x y 8z 2 2 2 16 GRÁFICO HIPERBOLÓIDE DE DUAS FOLHAS HIPERBOLÓIDE DE DUAS FOLHAS HIPERBOLÓIDE DE DUAS FOLHAS HIPERBOLÓIDE DE DUAS FOLHAS HIPERBOLÓIDE DE DUAS FOLHAS EXEMPLO Reduzir a equação à forma canônica, identificar e construir o gráfico da quádrica que ela representa: 4x y 8z 2 2 2 16 -4xx+yy-8zz=16 GRÁFICO DE OUTRO ÂNGULO SUPERFÍCIES QUÁDRICAS NÃO CENTRADAS PARABOLÓIDE ELÍPTICO PARABOLÓIDE ELÍPTICO PARABOLÓIDE ELÍPTICO PARABOLÓIDE CIRCULAR PARABOLÓIDE ELÍPTICO EXEMPLO Reduzir a equação à forma canônica, identificar e construir o gráfico da quádrica que ela representa: x 2y z 0 2 2 xx+2yy-z=0 GRÁFICO EXEMPLO Reduzir a equação à forma canônica, identificar e construir o gráfico da quádrica que ela representa: x yz 2 2 0 xx+y+Zz=0 GRÁFICO PARABOLÓIDE HIPERBÓLICO Se nas equações (8) os coeficientes dos termos de segundo grau tiverem sinais contrários, a equação representa um parabolóide hiperbólico. PARABOLÓIDE HIPERBÓLICO PARABOLÓIDE HIPERBÓLICO PARABOLÓIDE HIPERBÓLICO PARABOLÓIDE HIPERBÓLICO EXEMPLO Reduzir a equação à forma canônica, identificar e construir o gráfico da quádrica que ela representa: 9 x 4 y 36 z 0 2 2 -9xx+4yy-36z=0 GRÁFICO SUPERFÍCIE CÔNICA SUPERFÍCIE CÔNICA SUPERFÍCIE CÔNICA SUPERFÍCIE CÔNICA SUPERFÍCIE CÔNICA EXEMPLO Reduzir a equação à forma canônica, identificar e construir o gráfico da quádrica que ela representa: x 4y Z 2 2 2 0 xx+4yy-zz=0 GRÁFICO SUPERFÍCIE CILÍNDRICA SUPERFÍCIE CILÍNDRICA SUPERFÍCIE CILÍNDRICA SUPERFÍCIE CILÍNDRICA SUPERFÍCIE CILÍNDRICA SUPERFÍCIE CILÍNDRICA FIM
Baixar